代码随想录二叉树 Java（三）

news2024/11/26 23:18:56

文章目录

  • （简单）501. 二叉搜索树中的众数
  • （*中等）236. 二叉树的最近公共祖先
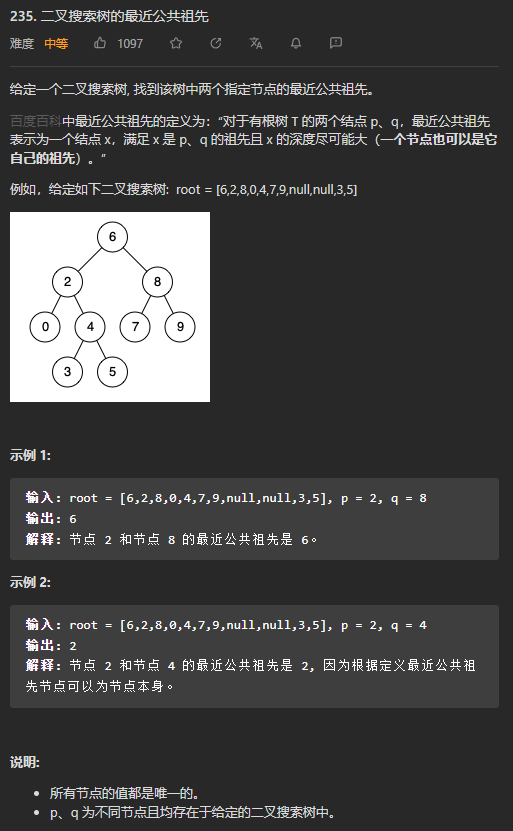
  • （中等）235. 二叉搜索树的最近公共祖先
  • （中等）701. 二叉搜索树中的插入操作
  • （*中等）450. 删除二叉搜索树中的节点
  • （*中等）669. 修剪二叉搜索树
  • （简单）108. 将有序数组转换为二叉搜索树
  • （中等）538. 把二叉搜索树转换为累加树

（简单）501. 二叉搜索树中的众数

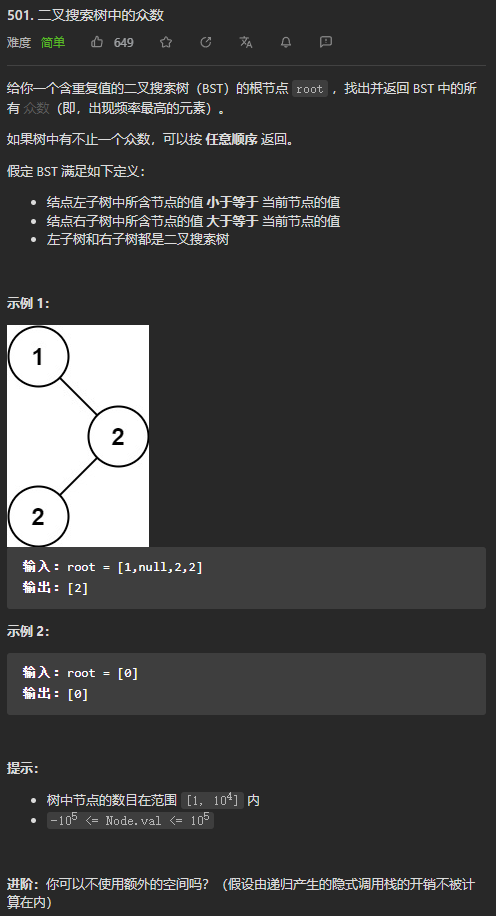
在这里插入图片描述

我的思路：先遍历二叉搜索树，将每个数值出现的次数使用HashMap进行记录，最后对HashMap按照value从大到小排序，把出现次数最多的数值添加到结果列表中，并返回。

这种做法，没有利用到二叉搜索树的特性，求一个普通二叉树中的众数也可以用这个方法。

import java.util.*;

class Solution {

    Map<Integer, Integer> map = new HashMap<>();

    public int[] findMode(TreeNode root) {
        inorder(root);
        ArrayList<Map.Entry<Integer, Integer>> entries = new ArrayList<>(map.entrySet());
        entries.sort((o1, o2) -> o2.getValue() - o1.getValue());
        ArrayList<Integer> resList = new ArrayList<>();
        resList.add(entries.get(0).getKey());
        int val = entries.get(0).getValue();
        for (int i = 1; i < entries.size(); i++) {
            if (entries.get(i).getValue() != val) {
                break;
            }
            resList.add(entries.get(i).getKey());
        }
        int[] res = new int[resList.size()];
        for (int i = 0; i < res.length; i++) {
            res[i] = resList.get(i);
        }
        return res;
    }

    public void inorder(TreeNode root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        map.put(root.val, map.getOrDefault(root.val, 0) + 1);
        inorder(root.right);
    }
}

在这里插入图片描述
其他思路，中序遍历

朴素的做法：因为这棵树的中序遍历是一个有序的序列，所以可以先获得这棵树的中序遍历，然后扫描这个中序遍历序列，然后用一个哈希表来统计每个数字出现的个数，这样就可以找到出现次数最多的数字。但是这样做的空间复杂度显然不是O(1)，原因是哈希表和保存中序遍历序列的空间代价都是O(n)

首先，考虑在寻找出现次数最多的数时，不使用哈希表。这个优化是基于二叉搜索树中序遍历的性质：一棵二叉搜索树的中序遍历序列是一个非递减的有序序列。重复出现的数字一定是一个连续出现的。

顺序扫描中序遍历序列，用base记录当前的数字，用count记录当前数字重复的次数，用maxCount来维护已经扫描过的数当中出现最多的那个数字的出现次数，用answer数组记录出现的众数。每次扫描到一个新的元素：

  • 首先更新base和count
    • 如果该元素和base相等，那么count自增1
    • 否则将base更新为当前数字，count复位为1
  • 然后更新maxCount
    • 如果count==maxCount，说明当前数字base出现的次数等于当前众数出现的次数，将base加入answer数组
    • 如果count>maxCount，那么说明当前数字base出现的次数大于当前众数出现的次数，因此，需要将maxCount更新为count，清空answer数组后，将base加入answer数组

可以把过程写成一个update函数，这样在寻找出现次数最多的数字的时候就可以省去一个哈希表带来的空间消耗

考虑不存储中序遍历序列，在递归进行中序遍历的过程中，访问某节点时直接使用上面的update函数，升序了保存中序遍历序列的空间

import java.util.ArrayList;
import java.util.List;

class Solution {

    int base;
    int count;
    int maxCount;
    List<Integer> ans;

    public int[] findMode(TreeNode root) {
        count = 0;
        maxCount = 0;
        base = Integer.MIN_VALUE;
        ans = new ArrayList<>();

        inorder(root);

        int[] mode = new int[ans.size()];
        for (int i = 0; i < ans.size(); i++) {
            mode[i] = ans.get(i);
        }

        return mode;
    }

    public void inorder(TreeNode root) {
        if (root == null) {
            return;
        }
        inorder(root.left);
        update(root.val);
        inorder(root.right);
    }

    public void update(int val) {
        //中序遍历中的第一个节点
        if (base == Integer.MIN_VALUE) {
            //base记录该节点的值
            base = val;
            //目前该值出现次数为1
            count = 1;

        } else if (base == val) {
            //出现重复元素
            count++;
        } else {
            base = val;
            count = 1;
        }

        if (count == maxCount) {
            ans.add(val);
        } else if (count > maxCount) {
            ans.clear();
            ans.add(val);
            maxCount = count;
        }
    }
}

这个代码，如果当前节点值出现次数等于maxCount，就加入list中，在下一次执行update时，如果count继续往上加，那么，之前向list中添加到其他元素就不是众数，需要将list清空，再将当前节点值加入list

复杂度分析：

  • 时间复杂度：O(n)，遍历这棵二叉树的复杂度
  • 空间复杂度：O(n)，递归的栈空间的空间代价
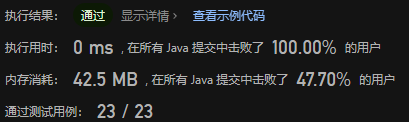
    在这里插入图片描述

（*中等）236. 二叉树的最近公共祖先

在这里插入图片描述

我的思路

采用层序遍历的方式，使用ArrayList记录要找的节点的所有祖先，然后从前往后比对，两个list中最后一个相同的节点就是这两个节点的最近公共祖先

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

class Solution {

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<TreeNode> list1 = findAllAncestor(root, p);
        List<TreeNode> list2 = findAllAncestor(root, q);
        TreeNode res = null;
        for (int i = 0, j = 0; i < list1.size() && j < list2.size(); i++, j++) {
            if (list1.get(i).val == list2.get(j).val) {
                res = list1.get(i);
            } else {
                break;
            }
        }
        return res;
    }

    //找到node节点的所有祖先，并返回
    public List<TreeNode> findAllAncestor(TreeNode root, TreeNode node) {

        Queue<List<TreeNode>> listQueue = new LinkedList<>();

        Queue<TreeNode> queue = new LinkedList<>();
        queue.add(root);

        ArrayList<TreeNode> list = new ArrayList<>();
        list.add(root);
        listQueue.add(list);

        while (!queue.isEmpty()) {
        	//当前节点
            TreeNode pollNode = queue.poll();
            //记录路径顺序的List
            List<TreeNode> pollList = listQueue.poll();
            if (pollNode.val == node.val) {
                return pollList;
            }
            if (pollNode.left != null) {
            	//还没有找到指定的节点，继续扩展该路径
                ArrayList<TreeNode> tmp = new ArrayList<>(pollList);
                tmp.add(pollNode.left);
                listQueue.add(tmp);
                queue.add(pollNode.left);
            }
            if (pollNode.right != null) {
                ArrayList<TreeNode> tmp = new ArrayList<>(pollList);
                tmp.add(pollNode.right);
                listQueue.add(tmp);
                queue.add(pollNode.right);
            }
        }
        return null;
    }
}

在这里插入图片描述
其他思路，递归

递归遍历整棵二叉树，定义 f x f_x fx​表示x节点的子树中是否包含p节点或q节点，如果包含为true，否则为false。那么符合条件的最近公共祖先x一定满足如下条件：

( f l s o n & & f r s o n ) ∣ ∣ ( ( x = p ∣ ∣ x = q ) & & ( f l s o n ∣ ∣ f r s o n ) ) (f_{lson} \&\& f_{rson}) || ((x=p||x=q)\&\&(f_{lson}||f_{rson})) (flson​&&frson​)∣∣((x=p∣∣x=q)&&(flson​∣∣frson​))

其中lson和rson分别代表x节点的左孩子和右孩子。

先看左边第一个条件
( f l s o n & & f r s o n ) (f_{lson} \&\& f_{rson}) (flson​&&frson​)
表示，x节点的左孩子和右孩子均包含p节点或q节点，如果左子树包含的是p节点，那么右子树只能包含q节点，反之亦然，因为p和q节点都是不同且唯一的节点，因此，如果满足这个条件，就可以说x是最近的公共祖先

再看右边第二个条件
( ( x = p ∣ ∣ x = q ) & & ( f l s o n ∣ ∣ f r s o n ) ) ((x=p||x=q)\&\&(f_{lson}||f_{rson})) ((x=p∣∣x=q)&&(flson​∣∣frson​))

这个条件考虑了x恰好是p节点或者q节点，且它的左子树或右子树包含了另一个节点，因此，如果满足这个判断条件，也可以说明x是部门要找的最近的公共祖先

该算法是自底向上从叶子节点开始更新的，所以，在所有满足条件的公共祖先中一定是深度最大的祖先先被访问到。在找到最近公共祖先x以后， f x f_x fx​按定义被设置为true，即假定这个子树只有一个p节点或者q节点，因此其他公共祖先不会在被判断为符合条件。

class Solution {

    TreeNode ans;

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root, p, q);
        return ans;
    }

	//dfs方法的含义是：以root为根节点的子树中是否包含节点p和q
	//对于叶子节点来说，lson和rson都是false
    public boolean dfs(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return false;
        }
        boolean lson = dfs(root.left, p, q);
        boolean rson = dfs(root.right, p, q);
        if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) {
            ans = root;
        }
        return lson || rson || (root.val == p.val || root.val == q.val);
    }
}

复杂度分析：

  • 时间复杂度：O(N)，其中N是二叉树的节点数，二叉树的所有节点有且只会被访问一次，因此时间复杂度是O(N)
  • 空间复杂度：O(N)，其中N是二叉树的节点数，递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为N，因此空间复杂度为O(N)
    在这里插入图片描述
    其他思路：存储父节点

可以使用哈希表存储所有节点的父节点，利用父节点的信息从p节点开始不断往上跳，并记录以及访问过的节点，再从q节点不断往上跳，如果碰到已经访问过的节点，那么这个节点就是要找的最近公共祖先。

具体步骤：

  1. 从根节点开始遍历整棵二叉树，用哈希表记录每个节点的父节点指针
  2. 从p节点开始不断往它的祖先移动，并用数据结构记录已经访问过的祖先节点
  3. 同样，从q节点开始不断往它的祖先移动，如果有祖先已经被访问过，即意味着该节点是p和q的最近公共祖先
import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;

class Solution {

    Map<Integer, TreeNode> map = new HashMap<>();
    Set<Integer> set = new HashSet<>();

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        dfs(root);
        while (p != null) {
            set.add(p.val);
            p = map.get(p.val);
        }
        while (q != null) {
            if (set.contains(q.val)) {
                return q;
            }
            q = map.get(q.val);
        }
        return null;
    }

    public void dfs(TreeNode root) {
        if (root.left != null) {
            map.put(root.left.val, root);
            dfs(root.left);
        }
        if (root.right != null) {
            map.put(root.right.val, root);
            dfs(root.right);
        }
    }
}

复杂度分析：

  • 时间复杂度：O(N)，其中N是二叉树的节点数。二叉树的所有节点有且只会被访问一次，从p和q节点往上跳，经过的祖先节点的个数不会超过N，因此，总的时间复杂度是O(N)
  • 空间复杂度：O(N)，其中N是二叉树的节点数。递归调用的栈的深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为N，因此空间复杂度为O(N)，哈希表存储每个节点的父节点也需要O(N)的空间复杂度，因此，总的空间复杂度是O(N)

在这里插入图片描述

（中等）235. 二叉搜索树的最近公共祖先

在这里插入图片描述

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (p.val < root.val && q.val < root.val) {
            return lowestCommonAncestor(root.left, p, q);
        }
        if (p.val > root.val && q.val > root.val) {
            return lowestCommonAncestor(root.right, p, q);
        }
        return root;
    }
}

在这里插入图片描述

其他思路，方法一：两次遍历

题目中保证了p和q是不同节点且均存在于给定的二叉搜索树中。所以，一定可以找到从根节点到p和从根节点到q的路径。

当我们分别得到了从根节点到p和q的路径之后，就可以很方便的找到它们的最近公共祖先了。显然，p和q的最近公共祖先就是从根节点到它们路径上的【分岔点】，也就是最后一个相同的节点。因此，从根节点到p的路径为数组path_p，从根节点到q的路径为数组path_q，只要找到最大的编号i，使得i满足path_p[i]=path_q[i]，那么对应的节点就是【分岔点】，即p和q的最近公共祖先就是path_p[i]

import java.util.ArrayList;
import java.util.List;

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        List<TreeNode> path_p = getPath(root, p);
        List<TreeNode> path_q = getPath(root, q);
        TreeNode ancestor = null;
        for (int i = 0; i < path_p.size() && i < path_q.size(); i++) {
            if (path_p.get(i) == path_q.get(i)) {
                ancestor = path_p.get(i);
            } else {
                break;
            }
        }
        return ancestor;
    }

    public List<TreeNode> getPath(TreeNode root, TreeNode target) {
        ArrayList<TreeNode> path = new ArrayList<>();
        TreeNode node = root;
        while (node != target) {
            path.add(node);
            if (target.val > node.val) {
                node = node.right;
            } else {
                node = node.left;
            }
        }
        path.add(node);
        return path;
    }
}

复杂度分析：

  • 时间复杂度：O(n)，其中n是给定二叉搜索树中的节点个数。上述代码需要的时间与节点p和q在书中的深度线性相关，而最坏情况下，树呈现链式结构，p和q一个是树的唯一的叶子节点，一个是该叶子节点的父节点，此时时间复杂度为O(n)
  • 空间复杂度：O(n)，需要存储根节点到p和q的路径，和上面分析方法相同，在最坏情况下，路径的长度为O(n)
    在这里插入图片描述
    其他思路，方法二：一次遍历

上面方法通过遍历找出到达节点p和q的路径，一共需要两次遍历。

也可以考虑将这两个节点放在一起遍历。

  • 从根节点开始遍历
  • 如果当前节点值大于p和q的值，说明p和q应该在当前节点的左子树，因此将当前节点移动到它的左子节点
  • 如果当前节点值小于p和q的值，说明p和q应该在当前节点的右子树，因此将当前节点移动到它的右子节点
  • 如果当前节点的值不满足上述两个条件，则说明当前节点就是分岔点。此时，p和q要么在当前节点的不同子树中，要么其中一个就是当前的节点。
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {

        TreeNode ancestor = root;
        while (true) {
            if (p.val < ancestor.val && q.val < ancestor.val) {
                ancestor = ancestor.left;
            } else if (p.val > ancestor.val && q.val > ancestor.val) {
                ancestor = ancestor.right;
            } else {
                break;
            }
        }
        return ancestor;
    }

}

复杂度分析：

  • 时间复杂度：O(n)，其中n是给定的二叉搜索树中的节点个数。分析思路与上一个方法一样。
  • 空间复杂度：O(1)
    在这里插入图片描述

（中等）701. 二叉搜索树中的插入操作

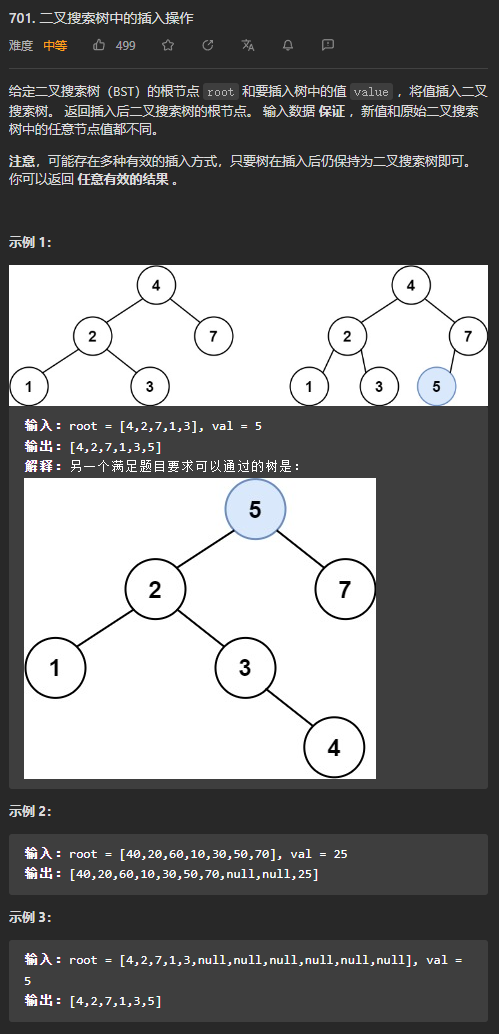
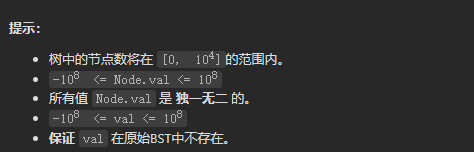
在这里插入图片描述
在这里插入图片描述
在本题的提示中，树中的节点数是可以为0的，也就意味着这一棵树为空，所以直接创建一个节点并返回即可。

如果根节点不为空，则将val从根节点开始比较，如果val的值大于根节点的值，则移动到该二叉树的右节点，如果val的值小于根节点，则移动到该二叉树的左节点，并使用一个变量pre记录当前节点的父节点。

在退出while循环时，node为空，需要在pre指向的节点上添加一个左子节点或者右子节点，如果val的值大于pre指向的节点，则给pre添加一个右子节点，如果val的值小于pre指向的节点，则给pre添加一个左子节点。

最后返回root。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }
        TreeNode node = root;
        TreeNode pre = null;
        while (node != null) {
            pre = node;
            if (val > node.val) {
                node = node.right;
            } else if (val < node.val) {
                node = node.left;
            }
        }
        if (val > pre.val) {
            pre.right = new TreeNode(val);
        } else {
            pre.left = new TreeNode(val);
        }
        return root;
    }
}

复杂度分析：

  • 时间复杂度：O(N)，其中N为树中节点的数目。最坏情况下，需要将值插入到树的最深的叶子节点上，而叶子节点最深为O(N)
  • 空间复杂度：O(1)，只使用了常数大小的空间

在这里插入图片描述

（*中等）450. 删除二叉搜索树中的节点

在这里插入图片描述
在这里插入图片描述
方法一，递归

二叉搜索树有以下性质：

  • 左子树的所有节点（如果有）的值均小于当前节点的值
  • 右子树的所有节点（如果有）的值均大于当前节点的值
  • 左子树和右子树均为二叉搜索树

二叉搜索树的题目基本上都可以用递归来解决。

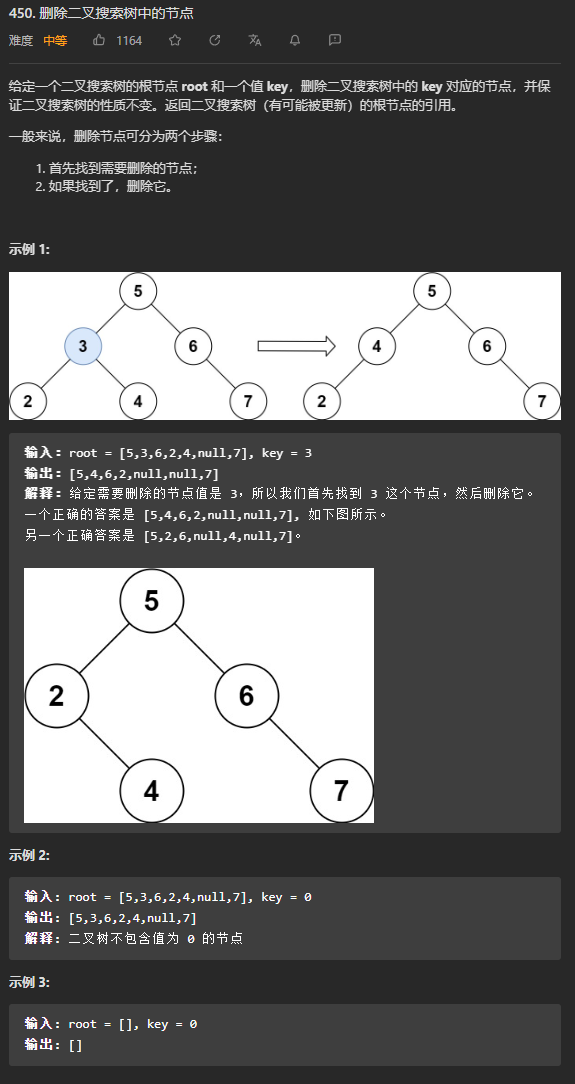
本题要求删除二叉树的节点，函数deleteNode的输入是二叉树的根节点root和一个整数key，输出是删除值为key的节点后的二叉树，并保持二叉树的有序性。按照以下情况分类讨论：

  • root为空，代表为搜索到值为key的节点，返回null
  • key < root.val，表示值为key的节点可能存在于root的左子树中，需要递归地在root.left调用deleteNode，并返回root
  • key > root.val，表示值为key的节点可能存在于root的右子树中，需要递归地在root.right调用deleteNode，并返回root
  • key == root.val，root即为要删除的节点。需要做的是：删除root，并将它的子树合并成一棵子树，保持有序性，并返回根节点。根据root的子树情况分成以下情况讨论：
    • root为叶子节点，没有子树。直接删除，返回空
    • root只有左子树，没有右子树。将它的左子树作为新的子树，返回它的左子节点
    • root只有右子树，没有左子树。将它的右子树作为新的子树，返回它的右子节点
    • root有左右子树，这是可将root的后继节点（比root大的最小节点，即它的右子树中的最小节点，即为successor）作为新的根节点代替root，并将successor从root的右子树中删除，使得在保持有序的情况下合并左右子树。

在代码实现上，先找到successor，再删除它。successor是root的右子树中的最小节点，可以先找到root的右子节点，在不停地往左子节点寻找，直到找到一个不存在左子节点的节点，这个节点即为successor。然后递归地在root.right调用deleteNode来删除successor。因为successor没有左子节点，因此这一步递归调用不会再次步入这一种情况。然后将successor更新为新的root并返回。

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        if (root == null) {
            return null;
        }
        //进入左子树查找
        if (key < root.val) {
            root.left = deleteNode(root.left, key);
            return root;
        }
        //进入右子树查找
        if (key > root.val) {
            root.right = deleteNode(root.right, key);
            return root;
        }
        //相等情况
        //情况1：叶子节点
        if (root.left == null && root.right == null) {
            return null;
        }

        //情况2：左子树不为空，右子树为空
        if (root.right == null) {
            return root.left;
        }

        //情况3：左子树为空，右子树不为空
        if (root.left == null) {
            return root.right;
        }


        //情况4：左子树和右子树都不为空
        TreeNode successor = root.right;
        //找到删除节点root的后继节点successor
        while (successor.left != null) {
            successor = successor.left;
        }

        //当要删除的节点都不为空时，把要删除节点的中序遍历下的后继节点移到被删除节点的位置，返回
        root.right = deleteNode(root.right, successor.val);
        successor.right = root.right;
        successor.left = root.left;
        return successor;
    }

}

如果要删除的节点，既有左子树，也有右子树，那么就先找到该节点在中序遍历中的后继节点successor，删除该节点，删除该节点的目的是为了让该节点取代被删除的节点的位置。之后把successor.right赋值为root.right，successor.left赋值为root.left，这样successor就取代了被删除的节点的根节点的位置，返回即可

如何找到successor，先获取当前根节点的右子节点，然后不断向左下角移动，直到某一节点没有左子节点（可能会有右子节点），那么该节点就是successor。

复杂度分析：

  • 时间复杂度：O(n)，其中n为root的节点个数。最差情况下，寻找和删除successor各需要遍历一次树。
  • 空间复杂度：O(n)，其中n为root的节点个数，递归的深度最深为O(n)。
    在这里插入图片描述
    方法二，迭代

方法一的递归深度最多为n，而大部分是由寻找值为key的节点贡献的，而寻找节点这一部分可以用迭代来优化。寻找并删除sucessor时，也可以使用一个变量保存它的父节点，从而可以节省一步递归操作。

（*中等）669. 修剪二叉搜索树

在这里插入图片描述

方法一，递归

对根节点root进行深度优先遍历。

对于当前访问的节点，如果节点为空节点，直接返回空节点。

如果节点的值小于low，那么说明该节点及它的左子树都不符合要求，返回他的右节点进行修剪后的结果。

如果节点的值大于high，那么说明该节点及它的右子树都不符合要求，返回它的左子树进行修剪后的结果。

如果节点的值位于区间[low,high]，将节点的左节点设为它的左子树修剪后的结果，右节点设为对它的右子树进行修剪后的结果。

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if (root == null) {
            return null;
        }
        if (root.val < low) {
            return trimBST(root.right, low, high);
        } else if (root.val > high) {
            return trimBST(root.left, low, high);
        } else {
            root.left = trimBST(root.left, low, high);
            root.right = trimBST(root.right, low, high);
            return root;
        }
    }
}

【注意】该棵树是二叉搜索树
如果某棵子树的根节点已经不在[low，high]的范围内，那么需要判断该根节点的值是小于low，还是大于high，如果小于low，那么，该节点的右子树中可能有符合条件的节点。如果大于high，那么，该节点的左子树中可能有符合条件的节点。

在看到这一题时，想借鉴 LeetCode 450 删除二叉搜索树中的节点 这一题的思路，也就是把不在规定区间内的节点都删掉，但是右考虑到二叉搜索树的性质，如果根节点已经小于low了，那么不用一个一个判断，它的左子节点肯定都不符合条件。一个一个删除太繁琐了。

复杂度分析：

  • 时间复杂度：O(n)，其中n是二叉树的节点数目
  • 空间复杂度： O(n)，当二叉树出现一条链的结构时，栈需要O(n)的空间。

在这里插入图片描述
方法二，迭代

如果一个节点node符合要求，即它的值位于区间[low,high]，那么它的左右子树该如何修剪？

先讨论一下左子树的修剪：

  • node的左节点为空节点，不需要修剪
  • node的左节点非空
    • 如果它的左节点left的值小于low，那么left以及left的左子树都不符合要求，将node的左节点设为left的右节点，然后重新对node的左节点进行判断
    • 如果左节点left的值大于等于low，又因为node的值已经符合要求，所以left的右子树一定符合要求。基于此，只需要对left的左子树进行修剪。令node = left，然后重新对node的左子树进行修剪。

以上过程可以迭代处理。对于右子树的修剪同理。

右子树的修剪：

  • node的右节点为空节点，不需要修剪
  • node的右节点非空
    • 如果它的右节点right大于high，那么right以及right的右子树都不符合要求，将node的右节点设为right的左节点，然后重新对node的右节点进行判断
    • 如果right的值小于等于high，又因为node的值已经符合要求，所以right的左子树一定符合要求。基于此，只需要对right的右子树进行修剪。令node = right，然后重新对node的右子树进行修剪
class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {


        //看根节点是否在[low,high]内
        while (root != null && (root.val < low || root.val > high)) {
            if (root.val < low) {
                //root以及root的左子树中的所有节点都不符合
                root = root.right;
            } else {
                //条件是root.val > high
                //root以及root的右子树中的所有节点都不符合
                root = root.left;
            }
        }

        if (root == null) {
            return null;
        }

        //修改左子树
        TreeNode node = root;
        while (node.left != null) {
            if (node.left.val < low) {
                node.left = node.left.right;
            } else {
                node = node.left;
            }
        }

        //修剪右子树
        node = root;
        while (node.right != null) {
            if (node.right.val > high) {
                node.right = node.right.left;
            } else {
                node = node.right;
            }
        }

        return root;
    }
}

复杂度分析：

  • 时间复杂度：O(n)，其中n为二叉树的节点数目。最多访问n个节点。
  • 空间复杂度：O(1)
    在这里插入图片描述

（简单）108. 将有序数组转换为二叉搜索树

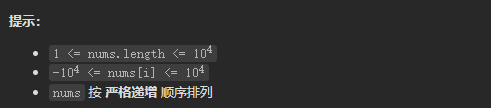
在这里插入图片描述
在这里插入图片描述

给定二叉搜索树的中序遍历，是否可以唯一地确定二叉搜索树？

不能。如果没有要求二叉搜索树的平衡高度。则任何一个数字都可以作为二叉搜索树的根节点，因此可能的二叉搜索树右多个。

如果增加一个限制条件，要求二叉搜索树的高度平衡，是否可以唯一地确定二叉搜索树？

不能。选择数组的中间数字作为二叉搜索树的根节点，这样分给左右子树的数字个数相同或者只相差1，可以使得树保持平衡。如果数组长度是奇数，则根节点的选择是唯一的，如果数组的长度是偶数，则可以选择中间位置左边的数字作为根节点或者中间位置右边的数字作为根节点，选择不同的数字作为根节点，则创建的平衡二叉搜索树也是不同的。

确定平衡二叉搜索树的根节点之后，其余的数字分别位于平衡二叉搜索树的左子树和右子树中，左子树和右子树分别也是平衡二叉搜索树，因此可以通过递归的方式创建平衡二叉搜索树。

递归的基准情形是平衡二叉搜索树不包含任何数字，此时平衡二叉搜索树为空。

在给定中序遍历序列数组的情况下，每一个子树中的数字在数组中一定是连续的，因此可以通过数组下标范围确定子树包含的数字，下标范围记为[left, right]。对于整个中序遍历序列，下标范围从left=0到right=nums.length-1。当left>right时，平衡二叉搜索树为空。

三种方法，都可以创建平衡的二叉搜索树：

  1. 总是选择中间位置左边的数字作为根节点
  2. 总是选择中间位置右边的数字作为根节点
  3. 选择任意一个中间位置数字作为根节点
class Solution {

    Random rand = new Random();

    public TreeNode sortedArrayToBST(int[] nums) {
        
        return build(nums, 0, nums.length - 1);
    }

    public TreeNode build(int[] nums, int left, int right) {
        if (left > right) {
            return null;
        }

        if (left == right) {
            return new TreeNode(nums[left]);
        }

        //选择中间位置左边的数字作为根节点
        //int mid = (left + right) / 2;

        //选择中间位置右边的数字作为根节点
        //int mid = (left + right + 1) / 2;

        //选择任意一个中间位置数字作为根节点
        int mid = (left + right + rand.nextInt(2)) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = build(nums, left, mid - 1);
        root.right = build(nums, mid + 1, right);
        return root;
    }
}

在这里插入图片描述

（中等）538. 把二叉搜索树转换为累加树

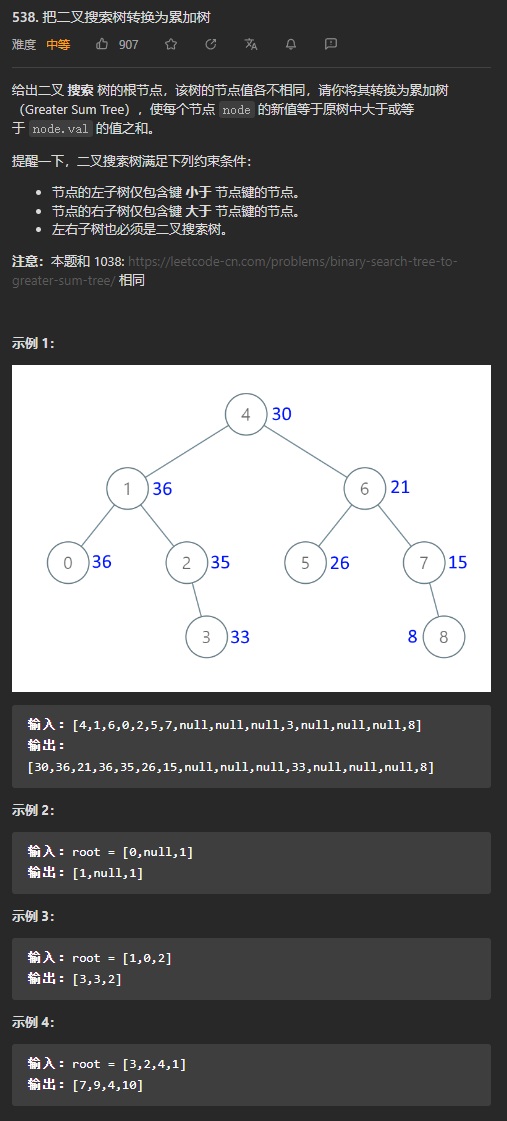
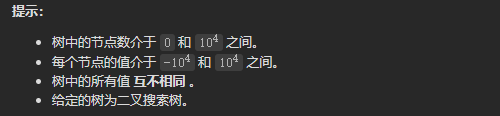
在这里插入图片描述
在这里插入图片描述
二叉搜索树是一棵空树，或者是具有以下列性质的二叉树：

  1. 若它的左子树不为空，则左子树上所有节点的值均小于它的根节点的值
  2. 若它的右子树不为空，则右子树上所有节点的值均大于它的根节点的值
  3. 它的左、右子树也分别为二叉搜索树

这样的性质可以发现，二叉搜索树的中序遍历是一个单调递增的有序序列。如果反序地中序遍历这棵二叉搜索树，即可以得到一个单调递减的有序序列

反向中序遍历

本题中要求我们将每个节点的值修改为原来地节点值加上所有大于它的节点值之和。这样只需要反序中序遍历该二叉搜索树，记录过程中的节点值之和，并不断更新当前遍历到的节点的值，即可得到题目要求的累加树。

class Solution {

    int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        order(root);
        return root;
    }

    public void order(TreeNode root) {
        if (root == null) {
            return;
        }
        order(root.right);
        sum += root.val;
        root.val = sum;
        order(root.left);
    }

}

class Solution {

    int sum = 0;

    public TreeNode convertBST(TreeNode root) {
        if (root != null) {
            convertBST(root.right);
            sum += root.val;
            root.val = sum;
            convertBST(root.left);
        }
        return root;
    }

}

复杂度分析：

  • 时间复杂度：O(n)，其中n是二叉搜索树的节点数。每个节点恰好被遍历一次。
  • 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为O(log n)，最坏情况下树呈现链状，为O(n)。
    在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/649585.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

软件测试中如何编写单元测试用例（白盒测试）

软件测试中如何编写单元测试用例（白盒测试）

目录 前言&#xff1a; 一、 单元测试的概念 二、开始测试前的准备 三、开始测试 四、完成测试 前言&#xff1a; 单元测试是软件测试中一种重要的测试方法&#xff0c;它是在代码级别进行测试&#xff0c;通过对每个模块或功能进行独立测试来保障代码的正确性和可靠性。…
阅读更多...
实验篇(7.2) 11. 站对站安全隧道 - 双方互相发起连接（FortiGate-IPsec） ❀ 远程访问

实验篇(7.2) 11. 站对站安全隧道 - 双方互相发起连接（FortiGate-IPsec） ❀ 远程访问

【简介】前面我们实验的是FortiClient客户端与防火墙进行VPN连接&#xff0c;现在我们要做的实验是防火墙与防火墙之间进行VPN连接。现在我们来看看两台防火墙之间要怎样创建VPN连接。 实验要求与环境 OldMei集团深圳总部部署了域服务器和ERP服务器&#xff0c;用来对集团总部进…
阅读更多...
【探索 Kubernetes|容器基础进阶篇 系列 3】容器进程的文件系统

【探索 Kubernetes|容器基础进阶篇 系列 3】容器进程的文件系统

文章目录 系列文章目录&#x1f479; 关于作者一、回顾二、容器进程的文件系统是什么样子的&#xff1f;rootfs一致性解决应用依赖关系解决复用性 三、OverlayFS 联合文件系统先决条件overlay2 驱动程序如何工作结构图探索含义-磁盘上的镜像层和容器层镜像层容器层 四、overlay…
阅读更多...
动态规划dp —— 26.环绕字符串中唯一的子字符串

动态规划dp —— 26.环绕字符串中唯一的子字符串

1.状态表示 是什么&#xff1f;dp表中里的值所表示的含义就是状态表示 dp[i]表示&#xff1a;以i位置元素为结尾的所有的子串里面&#xff0c;有多少个在base中出现过 2.状态转移方程 dp[i] 等于什么 如果是单个字母的子串&#xff0c;肯定会在base中出现&#xff0c;所以…
阅读更多...
一文详解！appium自动化测试

一文详解！appium自动化测试

目录 前言&#xff1a; Appinum前置知识 Andriod SDK 元素获取—UI Automator adb命令实践 adb常用命令 小结 Package与Activity Activity页面布局元素 monkey简介 monkey事件 操作事件简介 monkey参数 事件类参数 约束类参数 调试类参数 Monkey参数应用综合案…
阅读更多...
生成式AI - 关键技术历史和发展

生成式AI - 关键技术历史和发展

✈️当谈及生成式人工智能&#xff08;AI&#xff09;&#xff0c;我们进入了一个令人惊叹的领域&#xff0c;它不仅改变了我们与技术的互动方式&#xff0c;而且极大地推动了人工智能的发展。通过模仿人类创造力和想象力的能力&#xff0c;生成式AI引领着我们走向了全新的可能…
阅读更多...
re模块

re模块

目录 ❤ 正则表达式 常用正则 字符组 字符 量词 ❤ 正则表达式的使用 . ^ $ * ? { } 字符集&#xff3b;&#xff3d;&#xff3b;^&#xff3d; 分组 ()与 或 &#xff5c;&#xff3b;^&#xff3d; 转义符 \ 贪婪匹配 ❤ re模块 常量、属性 常用方法 re.co…
阅读更多...
echarts图表 的X轴添加滚动条

echarts图表 的X轴添加滚动条

1&#xff1a;原图 2&#xff1a;代码 dataZoom [{orient: horizontal,show: scoreShow,//控制滚动条显示隐藏realtime: true, //拖动滚动条时是否动态的更新图表数据height: 5, //滚动条高度start: 0, //滚动条开始位置&#xff08;共6等份&#xff09;end: this.endValue,//…
阅读更多...
复杂业务系统的通用架构设计法则

复杂业务系统的通用架构设计法则

一、什么是复杂系统 我们经常提到复杂系统&#xff0c;那么到底什么是复杂系统。我们看下维基的定义&#xff1a;复杂系统&#xff08;英语&#xff1a;complex system&#xff09;&#xff0c;又称复合系统&#xff0c;是指由许多可能相互作用的组成成分所组成的系统。强调了…
阅读更多...
Pytest教程__参数化（10）

Pytest教程__参数化（10）

pytest参数化有两种方式&#xff1a; mark的parametrize标记&#xff1a;pytest.mark.parametrize(变量名&#xff0c;变量值)&#xff0c;其中变量值类型为列表、元组或其它可迭代对象。fixture的params参数&#xff1a;pytest.fixture(params变量值)&#xff0c;其中变量值类…
阅读更多...
Selenium元素定位方法大全

Selenium元素定位方法大全

一、背景 作为当下最流行的web UI自动化测试工具&#xff0c;selenium是很多测试同学入门接触自动化测试时学习的第一个工具。想要自动化操作页面上的内容&#xff0c;元素定位是首先必须要学习的核心知识。 因此本文主要介绍selenium的几种最常用的元素定位方法&#xff0c;…
阅读更多...
008、体系架构之SQL 执行流程

008、体系架构之SQL 执行流程

SQL 执行流程 读取的执行写入的执行DDL的执行SQL运算SQL解析和编译SQL 层架构SQL 运算分布式 SQL 运算SQL 层架构 读取的执行 元数据的读取 执行器从information_schema当总获取表的元数据信息(table meta),元数据的信息从内存中读取就可以了&#xff0c;因为已经缓存到了info…
阅读更多...
Python抓取商品详情方法的几种方法比较

Python抓取商品详情方法的几种方法比较

抓取商品详情的方法有很多种&#xff0c;以下是其中几种常见的方法及其优缺点&#xff1a; 1.使用requests库发送HTTP请求&#xff0c;然后解析HTML或JSON格式的数据&#xff1a; 优点&#xff1a;这种方法可以抓取几乎所有网站上的数据&#xff0c;支持GET和POST请求&#xff…
阅读更多...
匿名内部类为什么泄漏，Lambda为什么不泄漏

匿名内部类为什么泄漏，Lambda为什么不泄漏

作者&#xff1a;麦客奥德彪 在Android开发中&#xff0c;内存泄露发生的场景其实主要就两点&#xff0c;一是数据过大的问题&#xff0c;而是调用与被调用生命周期不一致问题&#xff0c;对于对象生命周期不一致导致的泄漏问题占90%&#xff0c;最常见的也不好分析的当属匿名内…
阅读更多...
一段2个月工作经历没体现，美团背调没通过收回了offer

一段2个月工作经历没体现，美团背调没通过收回了offer

众所周知&#xff0c;很多公司在面试通过之后还会对求职者进行背景调查&#xff0c;这是企业确认求职者信息真实性的重要途径&#xff0c;具有减少信息不对称、降低用人风险等重要意义。 一般通过背景调查&#xff0c;如果企业了解到求职者劳动关系没有终止、解除、简历造假或…
阅读更多...
抖音的外卖服务商申请详细指南！

抖音的外卖服务商申请详细指南！

CKA-外卖服务商对外(5、6双月) 项目背景: 通过资源牵引助力商户交易增长&#xff0c;从组品、内容、流量等方面对客户进行1v1精细化辅导&#xff0c;帮助商户进行运营动作 的优化&#xff0c;以实现双月百万交易额的showcase打造&#xff0c;并以此完成“好商&#xff0c;好品…
阅读更多...
面了个00后的测试员，年薪20w问题基本都能回答上，必是刷了不少面试题···

面了个00后的测试员，年薪20w问题基本都能回答上，必是刷了不少面试题···

互联网行业竞争是一年比一年严峻&#xff0c;作为测试工程师的我们唯有不停地学习&#xff0c;不断的提升自己才能保证自己的核心竞争力从而拿到更好的薪水&#xff0c;进入心仪的企业&#xff08;阿里、字节、美团、腾讯等大厂.....&#xff09; 所以&#xff0c;大家就迎来了…
阅读更多...
从云端进行安全日志管理

从云端进行安全日志管理

随着企业变得越来越动态&#xff0c;需要一个灵活且易于访问的日志管理解决方案。Log360 Cloud 从本地和基于云的数据中收集您的网络日志&#xff0c;将其存储在云中&#xff0c;并通过多个实时/自动更新的图形仪表板实时提供网络安全的全面视图。 为什么选择云日志记录 随时…
阅读更多...
数据中心交换机和园区交换机有啥区别？

数据中心交换机和园区交换机有啥区别？

概要 在网络架构中&#xff0c;交换机是一种重要的设备&#xff0c;用于连接计算机、服务器和其他网络设备。随着不同领域的需求&#xff0c;交换机也有多种类型。本文将详细介绍数据中心交换机和园区交换机之间的区别&#xff0c;包括它们的原理和使用场景。 一. 数据中心交换…
阅读更多...
16.算法之字符串匹配算法

16.算法之字符串匹配算法

前言 字符串匹配是我们在程序开发中经常遇见的功能&#xff0c;比如sql语句中的like,java中的indexof,都是用来判断一个字符串是否包含另外一个字符串的。那么&#xff0c;这些关键字&#xff0c;方法&#xff0c;底层算法是怎么实现的么&#xff1f;本节&#xff0c;我们来探…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023