前言

字符串匹配是我们在程序开发中经常遇见的功能，比如sql语句中的like,java中的indexof,都是用来判断一个字符串是否包含另外一个字符串的。那么，这些关键字，方法，底层算法是怎么实现的么？本节，我们来探究一下，字符串匹配常见的算法。

1. 暴力匹配算法（BF）

1.1 算法思想

暴力匹配，顾名思义，就是逐个匹配主串和子串的字符，如果不一致，主串下标后移，重新比较，直到主串末尾，或者匹配到完整的子串。

1.2 代码验证

package org.wanlong.stringMatch;

/**
 * @author wanlong
 * @version 1.0
 * @description: 暴力匹配算法
 * @date 2023/6/8 9:51
 */
public class BF {

    public static boolean isMatch(String main, String sub) {
		//截取到子串前，后面没必要比较，因为长度都不够子串
		char[] subChars = sub.toCharArray();
        for (int i = 0; i < main.length() - sub.length(); i++) {
            //子串匹配
            String substring = main.substring(i, i + sub.length());
            char[] chars = substring.toCharArray();
            //是否完全匹配标志
            boolean flag = true;
            for (int j = 0; j < chars.length; j++) {
                if (chars[j] != subChars[j]) {
                    flag = false;
                    break;
                }
            }
            if (flag) {
                return true;
            }
        }

        return false;
    }
}

1.3 测试

@Test
public void testBF(){
    String str1="abcdefg";
    String str2="aabc";
    System.out.println(BF.isMatch(str1, str2));
}

运行结果：
false

1.4 时间复杂度

O(n*m)

1.5 应用场景

BF算法实现简单，易懂，在一些比较短的字符串匹配中，是可以使用的，但是当字符串长度较长时，性能会急剧下降。

2. RK算法

2.1 算法思想

RK 算法的全称叫 Rabin-Karp 算法，是由它的两位发明者 Rabin 和 Karp 的名字来命名的。我们知道，每次检查主串与子串是否匹配，需要依次比对每个字符，所以 BF 算法的时间复杂度就比较高，是O(n*m)。我们对朴素的字符串匹配算法稍加改造，引入哈希算法，时间复杂度立刻就会降低。

RK 算法的思路是这样的：我们通过哈希算法对主串中的 n-m+1 个子串分别求哈希值，然后逐个与模式串的哈希值比较大小。如果某个子串的哈希值与模式串相等，那就说明对应的子串和模式串匹配了（这里先不考虑哈希冲突的问题）。因为哈希值是一个数字，数字之间比较是否相等是非常快速的，所以模式串和子串比较的效率就提高了。

可以设计一个hash算法：

将字符串转化成整数，利用K进制的方式。
数字0-9： 10进制
123的拆解
100+20+3=123

假设我们字符串包含 大小写字母和0到9 十个数字，则可以设计如下：
小写字母a-z：26进制
大小写字母a-Z:52进制
十个数字0-9:62进制

以只是小写字母的26进制为例：

字符串“abc”转化成hash值的算法是：
a的ASCII码是97
b的ASCII码是98
c的ASCII码是99
97 \* 26^2+98 \* 26^1 +99\*26^0 =  65572+2548+99=68219
字符串 abc 转化成hash值是 68219，如果觉得计算太麻烦也可以从97开始，即ASCII-97字符串“abc”转化成hash值的算法是:(97-97)*262+(98-97)* 261 +(99-97)* 260+26+2=28

2.2 代码验证

package org.wanlong.stringMatch;

/**
 * @author wanlong
 * @version 1.0
 * @description: RK算法
 * @date 2023/6/8 20:04
 */
public class RK {

    public static boolean isMatch(String main, String sub) {

        //算出子串的hash值
        int hash_sub = strToHash(sub);
        for (int i = 0; i <= (main.length() - sub.length()); i++) {
            // 主串截串后与子串的hash值比较
            if (hash_sub == strToHash(main.substring(i, i + sub.length()))) {
                return true;
            }
        }


        return false;
    }

    /**
     * 支持 a-z 二十六进制
     * 获得字符串的hash值
     *
     * @param src
     * @return
     */
    public static int strToHash(String src) {
        int hash = 0;
        for (int i = 0; i < src.length(); i++) {
            hash *= 26;
            hash += src.charAt(i) - 97;
        }
        return hash;
    }

}

2.3 测试验证

@Test
public void testRK(){
    String str1="abcdefg";
    String str2="aabc";
    System.out.println(RK.isMatch(str1, str2));
}

2.4 适用场景

2.4.1 时间复杂度

RK 算法的的时间复杂度为O(m+n)
m:为匹配串长度
n:为主串长度

2.4.2 应用

适用于匹配串类型不多的情况，比如：字母、数字或字母加数字的组合 62 (大小写字母+数字)

3. BM算法

BF 算法性能会退化的比较严重，而 RK 算法需要用到哈希算法，而设计一个可以应对各种类型字符的哈希算法并不简单。BM（Boyer-Moore）算法。它是一种非常高效的字符串匹配算法，滑动算法。

3.1 算法思想

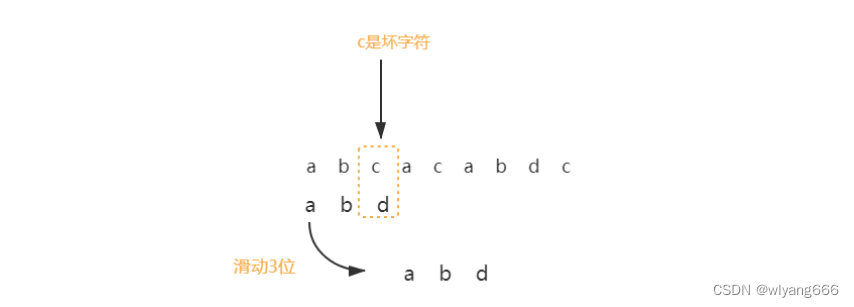
在这里插入图片描述
如上图，在上面的例子里，主串中的 c，在模式串中是不存在的。所以，模式串向后滑动的时候，只要 c 与模式串有重合，肯定无法匹配。所以，我们可以一次性把模式串往后多滑动几位，把模式串移动到 c 的后面。

BM 算法，本质上其实就是在寻找这种规律。借助这种规律，在模式串与主串匹配的过程中，当模式串和主串某个字符不匹配的时候，能够跳过一些肯定不会匹配的情况，将模式串往后多滑动位。

3.2 算法原理

BM算法包含两部分，分别是坏字符规则和好后缀规则

3.2.1 坏字符规则

BM 算法的匹配顺序比较特别，它是按照模式串下标从大到小的顺序，倒着匹配的。

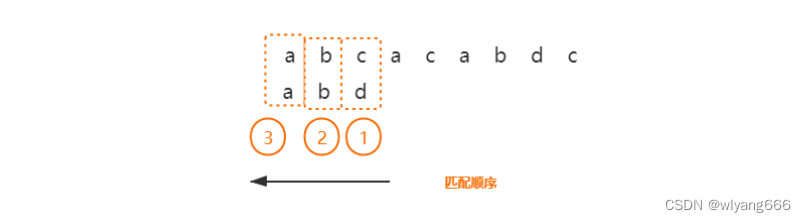
在这里插入图片描述
我们从模式串的末尾往前倒着匹配，当我们发现某个字符没法匹配的时候。我们把这个没有匹配的字符叫作坏字符（主串中的字符）。

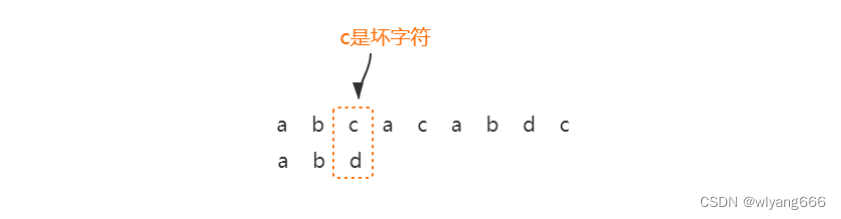
字符 c 与模式串中的任何字符都不可能匹配。这个时候，我们可以将模式串直接往后滑动三位，将模式串滑动到 c 后面的位置，再从模式串的末尾字符开始比较。
在这里插入图片描述
坏字符 a 在模式串中是存在的，模式串中下标是 0 的位置也是字符 a。这种情况下，我们可以将模式串往后滑动两位，让两个 a 上下对齐，然后再从模式串的末尾字符开始，重新匹配。

当发生不匹配的时候，我们把坏字符对应的模式串中的字符下标记作 si。如果坏字符在模式串中存在，我们把这个坏字符在模式串中的下标记作 xi。如果不存在，我们把 xi 记作 -1。那模式串往后移动的位数就等于。（下标，都是字符在模式串的下标）
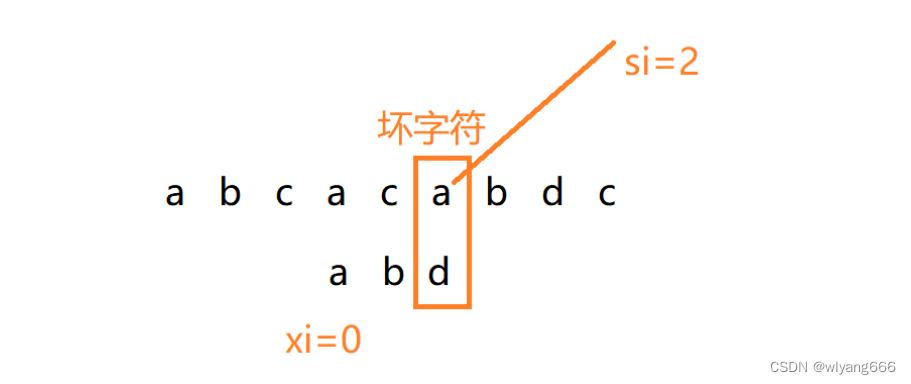
在这里插入图片描述
那么，按照如上规律可得：

第一次移动3位
c在模式串中不存在，所以xi = -1，移动位数 n =2-(-1)=3
第二次移动2位
a在模式串中存在，所以xi = 0，移动位数n =2-0=2

3.2.2 好后缀规则

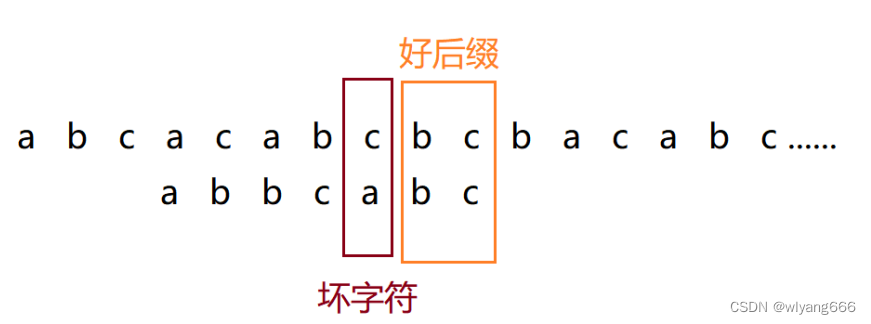
在这里插入图片描述
我们把已经匹配的我们拿它在模式串中查找，如果找到了另一个跟{u}相匹配的子串{u*}，那我们就将模式串滑动到子串{u*}与主串中{u}对齐的位置。

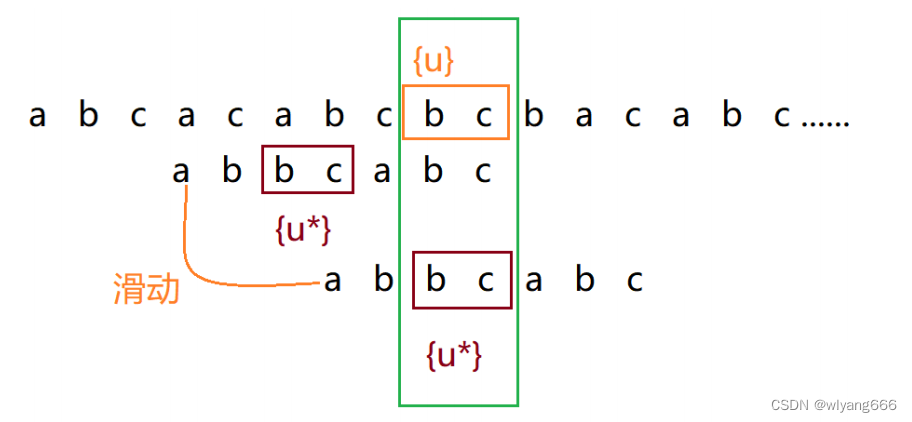
如果在模式串中找不到另一个等于{u}的子串，我们就直接将模式串，滑动到主串中{u}的后面，因为之前的任何一次往后滑动，都没有匹配主串中{u}的情况
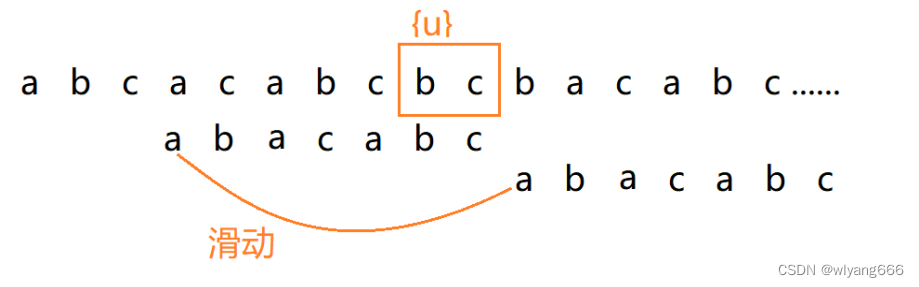
在这里插入图片描述
但是有种 过度滑动 情况要考虑，如下图所示：

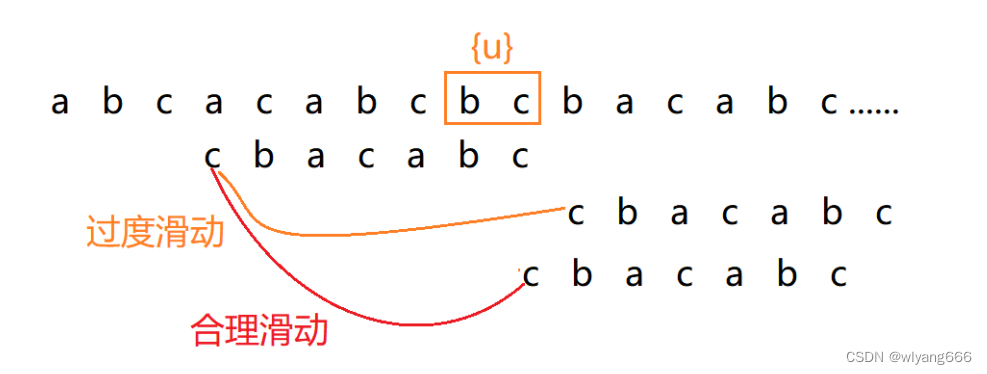
当模式串滑动到前缀与主串中{u}的后缀有部分重合的时候，并且重合的部分相等的时候，就有可能会存在完全匹配的情况。
以上面的模式串为例，模式串的前缀c与主串u的后缀 c 相等，此时不能过度滑动。

所以，针对这种情况，我们不仅要看 好后缀 在模式串中，是否有另一个匹配的子串，我们还要考察好后缀的后缀子串（c），是否存在跟模式串的前缀子串（c）匹配的。

如何选择坏字符和好后缀？

其实仔细思考，不管是好后缀，还是坏字符，都是为了让我们尽最大可能的避免重复进行字符比较匹配，从而降低时间复杂度。我们可以分别计算好后缀和坏字符往后滑动的位数，然后取两个数中最大的，作为模式串往后滑动的位数。

如果我们拿坏字符，在模式串中顺序遍历查找，这样就会比较低效。可以采用散列表，我们可以用一个256数组，来记录每个字符在模式串中的位置，数组下标可以直接对应字符的ASCII码值，数组的值为字符在模式串中的位置，没有的记为-1

这里散列表的作用是：根据字符的ascll 码，能直接计算到他在模式串中最后一次出现的位置，我们知道，哈希表查询的时间复杂度是O(1)。

如下图所示：

bc[97]=a
bc[98]=b
bc[100]=d
有重复的字母以后面的位置为准。
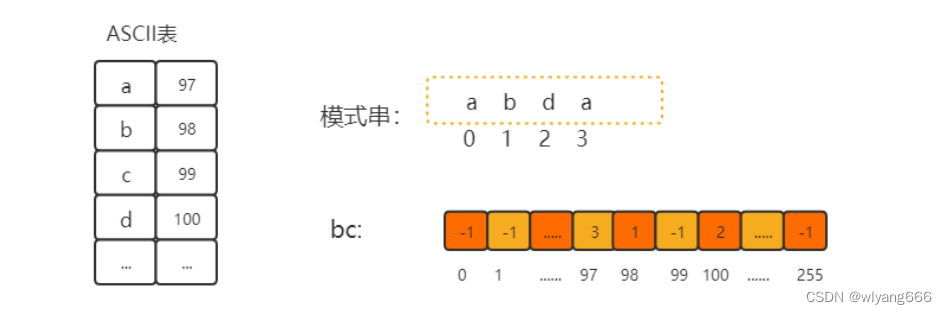
在这里插入图片描述

3.3 代码验证


package org.wanlong.stringMatch;

/**
 * @author wanlong
 * @version 1.0
 * @description: BM算法验证
 * @date 2023/6/12 10:31
 */
public class BM {

    // 哈希表长度
    private static final int SIZE = 256;


    /**
     * @Description: 构建坏字符哈希表
     * @Author: wanlong
     * @Date: 2023/6/15 14:17
     * @param b: 模式串
     * @param m: 模式串长度
     * @param dc: 哈希表
     * @return void
     **/
    private static void generateBC(char[] b, int m, int[] dc) {
        for (int i = 0; i < SIZE; ++i) {
            // 初始化 dc 模式串中没有的字符值都是-1
            dc[i] = -1;
        }
        //将模式串中的字符希写入到字典中
        for (int i = 0; i < m; ++i) {
            int ascii = (int) b[i]; // 计算 b[i] 的 ASCII 值
            dc[ascii] = i;
        }
    }

    /**
     * @Description: 坏字符规则
     * @Author: wanlong
     * @Date: 2023/6/15 14:14
     * @param a: 主串
     * @param b: 模式串
     * @return boolean
     **/
    public static boolean bad(char[] a, char[] b) {
        //主串长度
        int n = a.length;
        //模式串长度
        int m = b.length;
        //创建字典
        int[] bc = new int[SIZE];
        // 构建坏字符哈希表，记录模式串中每个字符最后出现的位置
        generateBC(b, m, bc);
        // i表示主串与模式串对齐的第一个字符
        int i = 0;
        while (i <= n - m) {
            int j;
            for (j = m - 1; j >= 0; --j) {
                // 模式串从后往前匹配
                //i+j ： 不匹配的位置
                if (a[i + j] != b[j])
                    // 坏字符对应模式串中的下标是j
                    break;
            }
            if (j < 0) {
                // 匹配成功，i是主串与模式串第一个匹配的字符的位置
                return true;
            }
            // 这里等同于将模式串往后滑动j-bc[(int)a[i+j]]位
            // si：j
            // xi：bc[(int)a[i+j]]
            i = i + (j - bc[(int) a[i + j]]);
        }
        return false;
    }
}

3.4 测试验证

@Test
public void testBM(){
    String str1="abcabcabc";
    String str2="ab";
    System.out.println(BM.bad(str1.toCharArray(), str2.toCharArray()));
}

3.5 时间复杂度

BM算法的时间复杂度是O(N/M)
n:主串长度
m:模式串长度

3.6 适用场景

BM算法比较高效，在实际开发中，特别是一些文本编辑器中，用于实现查找字符串功能。

4. 字典树

4.1 算法思想

Trie 树，也叫“字典树”。它是一个树形结构。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。
比如：有 6 个字符串，它们分别是：how，hi，her，hello，so，see，我们可以将这六个字符串组成
Trie树结构。
Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。

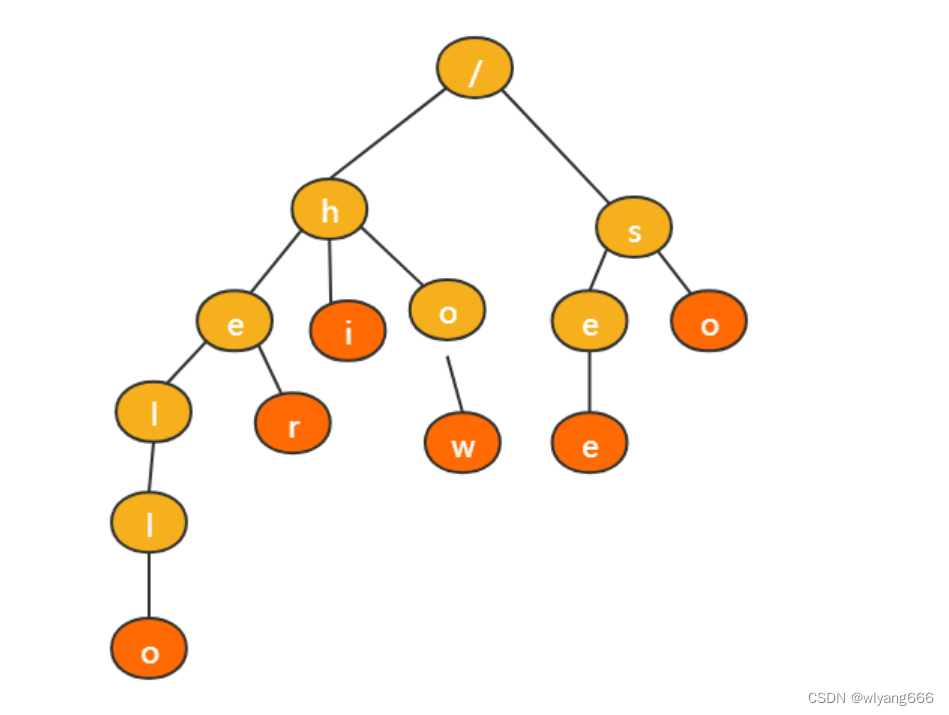
在这里插入图片描述
其中，根节点不包含任何信息。每个节点表示一个字符串中的字符，从根节点到红色节点的一条路径表
示一个字符串（红色节点为叶子节点）

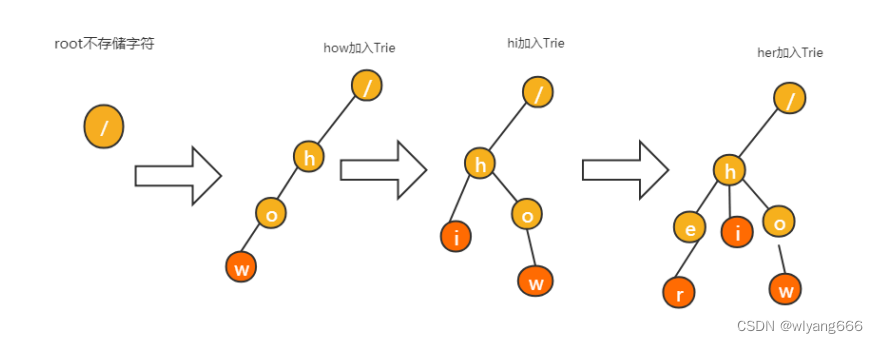
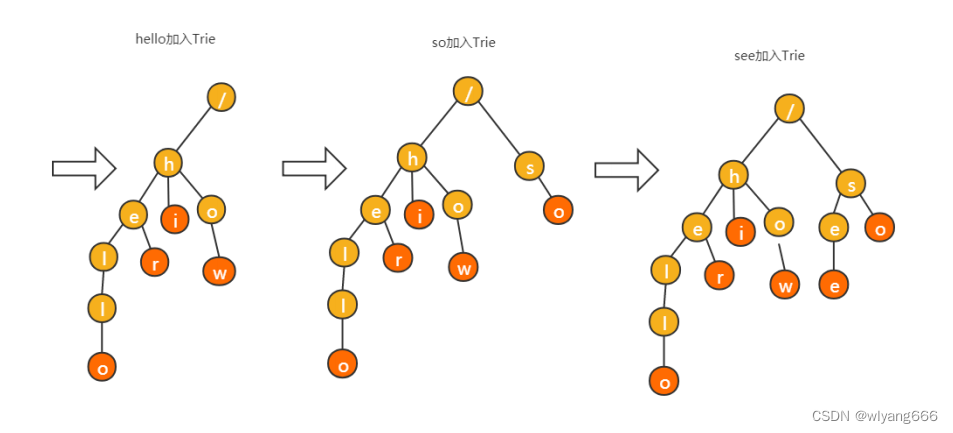
Trie 树是一个多叉树
我们通过一个下标与字符一一映射的数组，来存储子节点的指针

假设我们的字符串中只有从 a 到 z 这 26 个小写字母，我们在数组中下标为 0 的位置，存储指向子节点a 的指针，下标为 1 的位置存储指向子节点 b 的指针，以此类推，下标为 25 的位置，存储的是指向的子节点 z 的指针。如果某个字符的子节点不存在，我们就在对应的下标的位置存储 null。
在这里插入图片描述
当我们在 Trie 树中查找字符串的时候，我们就可以通过字符的 ASCII 码减去“a”的 ASCII 码，迅速找到
匹配的子节点的指针。比如，d 的 ASCII 码减去 a 的 ASCII 码就是 3，那子节点 d 的指针就存储在数组
中下标为 3 的位置中

如果要在一组字符串中，频繁地查询某些字符串，用 Trie 树会非常高效。构建 Trie 树的过程，需要扫描所有的字符串，时间复杂度是 O(n)（n 表示所有字符串的长度和）。但是一旦构建成功之后，后续的查询操作会非常高效。每次查询时，如果要查询的字符串长度是 k，那我们只需要比对大约 k 个节点，就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说，构建好 Trie 树后，在其中查找字符串的时间复杂度是 O(k)，k 表示要查找的字符串的长度。

4.2 代码验证

4.2.1 定义树节点类

package org.wanlong.stringMatch;

public class TrieNode {
    public char data;
    public TrieNode[] children = new TrieNode[26];
    //是否叶子节点标识
    public boolean isEndingChar = false;

    public TrieNode(char data) {
        this.data = data;
    }
}

4.2.2 定义字典树类

package org.wanlong.stringMatch;

/**
 * @author wanlong
 * @version 1.0
 * @description: 字典树
 * @date 2023/6/15 10:34
 */
public class Trie {

    private TrieNode root = new TrieNode('/'); // 存储无意义字符

    // 往Trie树中插入一个字符串
    public void insert(char[] text) {
        TrieNode p = root;
        for (int i = 0; i < text.length; ++i) {
            int index = text[i] - 97;
            if (p.children[index] == null) {
                TrieNode newNode = new TrieNode(text[i]);
                p.children[index] = newNode;
            }
            p = p.children[index];
        }
        //叶子节点打标签
        p.isEndingChar = true;
    }

    // 在Trie树中查找一个字符串
    public boolean find(char[] pattern) {
        TrieNode p = root;
        for (int i = 0; i < pattern.length; ++i) {
            int index = pattern[i] - 97;
            if (p.children[index] == null) {
                return false; // 不存在pattern
            }
            p = p.children[index];
        }
        if (!p.isEndingChar)
            // 不能完全匹配，只是前缀
            return false; 
        else
            // 找到pattern
            return true; 
    }

}

4.3 测试验证

@Test
public void testTrie(){
    Trie trie=new Trie();
    trie.insert("hello".toCharArray());
    trie.insert("her".toCharArray());
    trie.insert("hi".toCharArray());
    trie.insert("how".toCharArray());
    trie.insert("see".toCharArray());
    trie.insert("so".toCharArray());
    System.out.println(trie.find("how".toCharArray()));
}

4.4 时间复杂度

如果要在一组字符串中，频繁地查询某些字符串，用 Trie 树会非常高效。构建 Trie 树的过程，需要扫描所有的字符串，时间复杂度是 O(n)（n 表示所有字符串的长度和）。但是一旦构建成功之后，后续的查询操作会非常高效。每次查询时，如果要查询的字符串长度是 k，那我们只需要比对大约 k 个节点，就能完成查询操作。跟原本那组字符串的长度和个数没有任何关系。所以说，构建好 Trie 树后，在其中查找字符串的时间复杂度是 O(k)，k 表示要查找的字符串的长度。

4.5 适用场景

利用 Trie 树，实现搜索关键词的提示功能。

我们假设关键词库由用户的热门搜索关键词组成。我们将这个词库构建成一个 Trie 树。当用户输入其中某个单词的时候，把这个词作为一个前缀子串在 Trie 树中匹配。为了讲解方便，我们假设词库里只有hello、her、hi、how、so、see 这 6 个关键词。当用户输入了字母 h 的时候，我们就把以 h 为前缀的hello、her、hi、how 展示在搜索提示框内。当用户继续键入字母 e 的时候，我们就把以 he 为前缀的hello、her 展示在搜索提示框内。这就是搜索关键词提示的最基本的算法原理。
在这里插入图片描述