两数之和
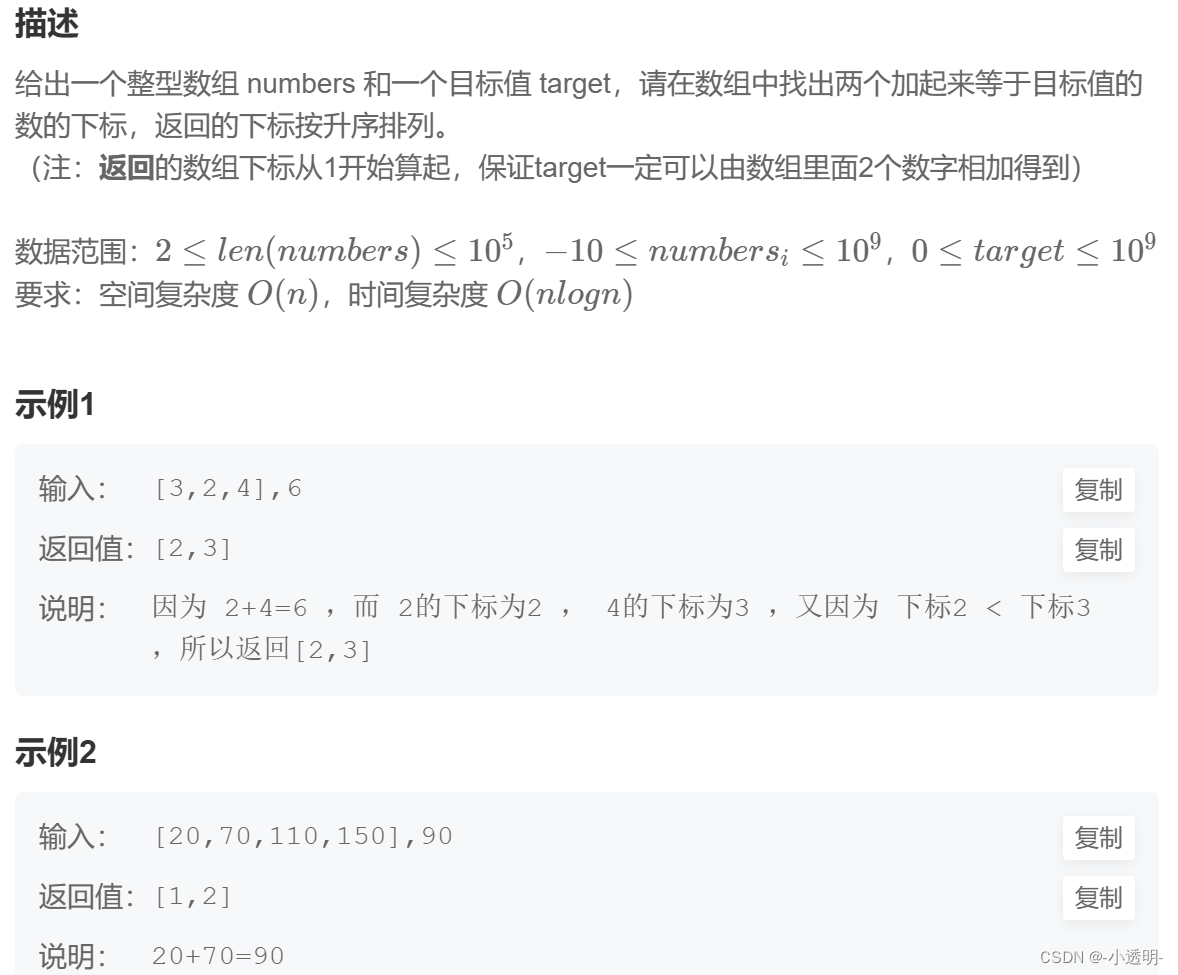
哈希表的思想
以空间换时间,这是由于哈希表保存了键值对,其查找复杂度为O(1)。
解题思路为
-
定义哈希表hashmap,其存放的键值对为<取值,下标>。
-
从开始处遍历数组,对于第i个位置,在哈希表中寻找target-nums[i]是否存在,若存在,将两个下标放入数组中返回;若不存在,将其添加至表中,继续遍历。
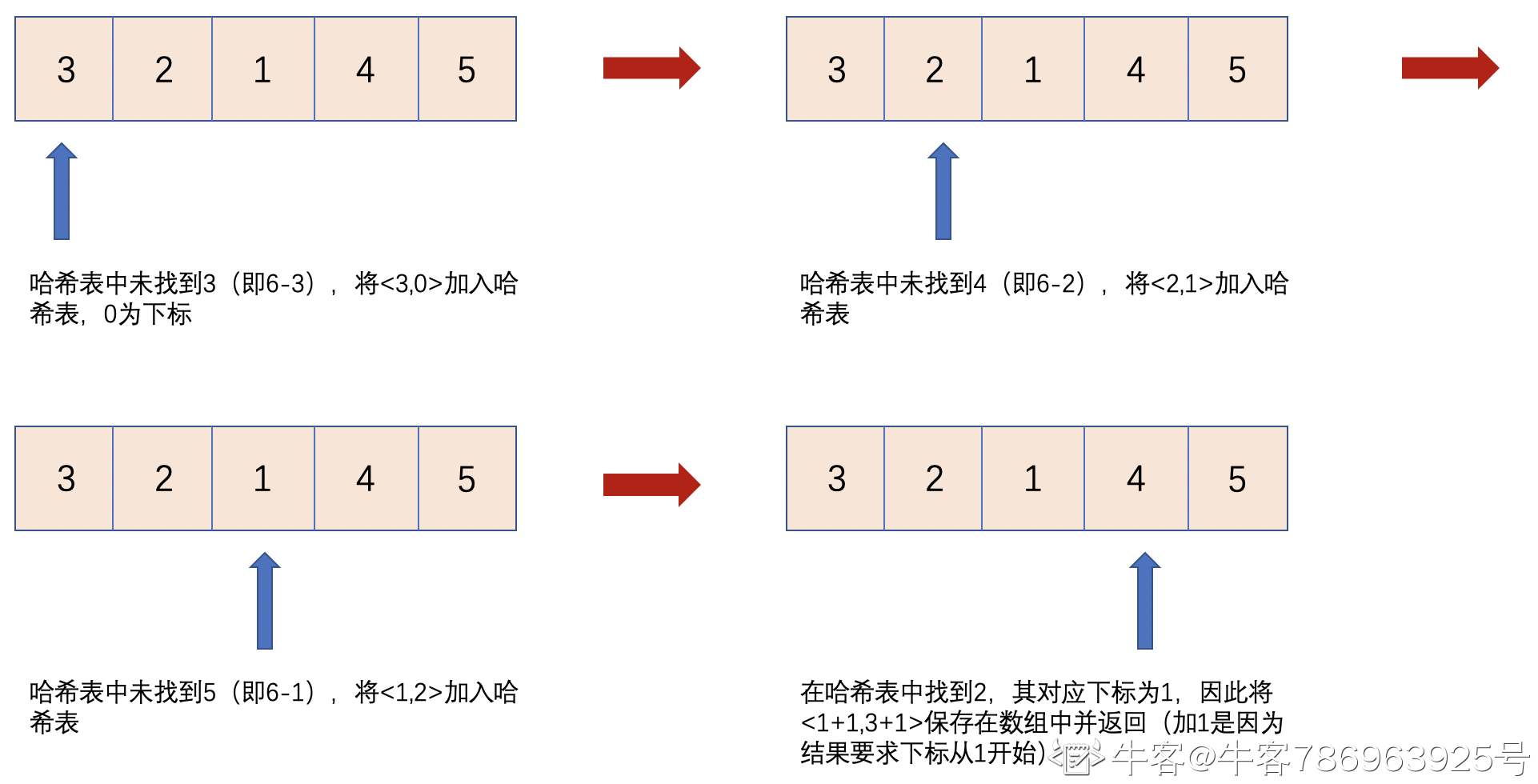
此解法只遍历数组一次,且在哈希表中查找的时间复杂度为O(1),因此总时间复杂度为O(N);
该方法需要构建哈希表,因此空间复杂度为O(N)。
#include <vector>
class Solution {
public:
/**
* @param numbers int整型vector
* @param target int整型
* @return int整型vector
*/
vector<int> twoSum(vector<int>& numbers, int target) {
vector<int> res;
if(numbers.size()==0) return res;
map<int, int> hash;//哈希表<值,下标>
for(int i=0; i<numbers.size(); i++){
if(hash[target-numbers[i]]){
res.push_back(hash[target-numbers[i]]);//找到了,说明该下标在遍历到的数之前(因为仅遍历数组一遍)
res.push_back(i+1);
return res;
}else hash[numbers[i]]=i+1;//下标从1开始
}
return res;
}
};数组中出现次数超过一半的数字
哈希(时间复杂度:O(n),空间复杂度:O(n))
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int> numbers) {
int len=numbers.size();
if(len==0) return -1;
if(len==1) return numbers[0];
map<int, int> hash;//哈希表<值,次数>
for(int i=0;i<len;i++) hash[numbers[i]]++;
for(int i=0;i<len;i++) {
if(hash[numbers[i]]>(len/2)) return numbers[i];
}
return 0;
}
};候选法(最优解)
假如数组中存在众数,那么众数一定大于数组的长度的一半。
思想:如果两个数不相等,就消去这两个数。最坏情况下,每次消去一个众数和一个非众数,那么如果存在众数,最后留下的数肯定是众数。
- 初始化:候选人cond = -1, 候选人的投票次数cnt = 0
- 遍历数组,如果cnt=0, 表示没有候选人,则选取当前数为候选人,++cnt
- 否则,如果cnt > 0, 表示有候选人,如果当前数=cond,则++cnt,否则--cnt
- 直到数组遍历完毕,最后检查cond是否为众数
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int> numbers) {
int len=numbers.size();
int cond=-1, cnt=0;
for(int i=0;i<len;i++){
if(cnt==0){
cond=numbers[i];//选取一个候选数
cnt++;
}else{
if(cond==numbers[i]) cnt++;
else cnt--;
}
}cnt=0;
for(int i=0;i<len;i++)
if(cond==numbers[i]) cnt++;
if(cnt>(len/2)) return cond;
return 0;
}
};数组中只出现一次的两个数字

#include <vector>
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* @param array int整型vector
* @return int整型vector
*/
vector<int> FindNumsAppearOnce(vector<int>& array) {
vector<int> res;
int len = array.size();
map<int, int>hash;
for(int i=0;i<len;i++) hash[array[i]]++;
for(int i=0;i<len;i++){
if(hash[array[i]]==1) res.push_back(array[i]);
} sort(res.begin(), res.end());//只有两个元素,可忽略不计
return res;
}
};缺失的第一个正整数

class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* @param nums int整型vector
* @return int整型
*/
int minNumberDisappeared(vector<int>& nums) {
map<int, int>hash;
for(int i=0;i<nums.size();i++) hash[nums[i]]++;
int res = 1;
while(hash.find(res)!=hash.end()) res++;//哈希表中有res
//或hash.count(res)的数值只有 0 和 1
return res;
}
};三数之和

- step 1:排除边界特殊情况。
- step 2:使用sort函数优先对其排序。
- step 3:得到有序数组后,遍历该数组,对于每个遍历到的元素假设它是三元组中最小的一个,那么另外两个一定在后面。
- step 4:需要三个数相加为0,则另外两个数相加应该为上述第一个数的相反数.可以利用双指针在剩余的子数组中找有没有这样的数对。双指针指向剩余子数组的首尾,如果二者相加为目标值,那么可以记录,而且二者中间的数字相加可能还会有(注意去重)。
- step 5:如果二者相加大于目标值,说明右指针太大了,那就将其左移缩小,相反如果二者相加小于目标值,说明左指针太小了,将其右移扩大,直到两指针相遇,剩余子数组找完了。
#include <vector>
class Solution {
public:
vector<vector<int> > threeSum(vector<int> &num) {
vector<vector<int>>res;
int len = num.size();
if(len < 3) return res;
sort(num.begin(), num.end());
for(int i=0;i<len-2;i++){
if(num[i] == num[i-1] && i!=0) continue;
int j=i+1, k=len-1;
while(j < k){
if(num[j] + num[k] + num[i] == 0){
res.push_back({num[i], num[j], num[k]});
while(k-1>j && num[k]==num[k-1]) k--;//去重
while(j+1<k && num[j]==num[j+1]) j++;//去重
j++, k--;
}
else if(num[j] + num[k] + num[i]>0) k--;
else j++;
}
}
return res;
}
};