Efficient Global 2D-3D Matching for Camera Localization in a Large-Scale 3D Map

1. 相似源码

由于paper并没有给出源码，我们找到了相似的源码：https://github.com/nadiawangberg/structure-based-visual-localization。

这是一个相机内部参数的文本文件，其中包含了一个内部参数矩阵K。该矩阵的元素用于将3D世界坐标系中的点转换为2D图像坐标系中的点。这个文件中的矩阵表示相机的内部参数，该矩阵的值在相机制造时被测量得到。

具体来说，这个文件中的每一行包含一个3×3的矩阵K。这个矩阵包含了相机的内部参数，它包括焦距、图像中心的偏移量和一个缩放因子。该矩阵用于将3D世界坐标系中的点投影到2D图像平面上。K矩阵中的值可以通过对相机进行标定（即在多个位置和朝向下拍摄一些图像，然后测量相机的参数）得到。

这里的K矩阵如下：

1520.4  0       302.32
0       1525.9  246.87
0       0       1

其中，第一行表示相机在水平方向上的焦距和图像中心的偏移量，第二行表示相机在竖直方向上的焦距和图像中心的偏移量，最后一行表示一个缩放因子和一个平移因子。

打印：
K1：相机1的内参矩阵
K2：相机2的内参矩阵
R: 从相机1到相机2的旋转矩阵，是一个3x3的矩阵。
t: 从相机1到相机2的平移向量，是一个3x1的列向量。

函数返回相机1和相机2的投影矩阵P1和P2，分别是3x4的矩阵。

P1和P2分别是相机1和相机2的投影矩阵，是一个3x4的矩阵。

在计算机视觉中，我们通常使用投影矩阵将三维空间中的点投影到相机坐标系下的二维图像平面上。对于一个三维点 $X = (X, Y, Z)$ ，它在相机坐标系下的表示为 $X_c=(X_c,Y_c,Z_c)$ 。那么，它在相机图像平面上的投影点 $p = (u, v)$ ，可以通过以下方式计算：
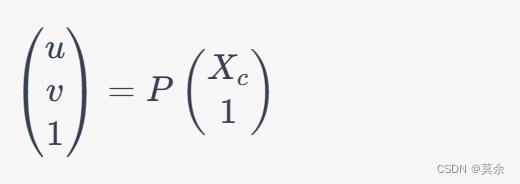
在这里插入图片描述

其中， $P$ 是投影矩阵，是一个3x4的矩阵。因此，对于相机1和相机2，它们的投影矩阵分别是 $P_1$ 和 $P_2$ 。

在这个函数中，我们根据相机1和相机2的内参矩阵 $K_1$ 和 $K_2$ 以及从相机1到相机2的旋转矩阵 $R$ 和平移向量 $t$ ，计算得到它们的投影矩阵 $P_1$ 和 $P_2$ 。这些投影矩阵可以用来将三维空间中的点投影到相应的二维图像平面上。

这是一个 Python 函数，它接受两个相机的内参矩阵（K1 和 K2），以及它们之间的旋转和平移（R 和 t），并计算出它们的投影矩阵 P1 和 P2。

第一个相机的投影矩阵 P1 是通过将内参矩阵 K1 与一个 3x4 的矩阵相乘得出的，这个 3x4 的矩阵的前三列是单位矩阵，第四列是零向量。这个 3x4 的矩阵表示从相机的 3D 坐标系到世界坐标系的转换。

第二个相机的投影矩阵 P2 是通过将内参矩阵 K2 与一个 3x4 的矩阵相乘得出的，这个 3x4 的矩阵的前三列是旋转矩阵 R，第四列是平移向量 t。这个 3x4 的矩阵表示从世界坐标系到第二个相机的 3D 坐标系的转换。

该函数返回投影矩阵 P1 和 P2，它们的形状都是 3x4。

第一个相机和第二个相机的坐标系通常是不同的，因为它们位于不同的位置和方向上。在三维空间中，我们通常使用世界坐标系来表示场景中的点和物体，而每个相机都有它自己的相机坐标系。

相机坐标系通常是相机的成像平面上的一个二维坐标系和相机光轴所构成的三维坐标系的结合。

在相机坐标系中，成像平面通常被定义为 $z = f$ 的平面，其中 $f$ 是相机的焦距。相机坐标系的 $x$ 轴通常指向成像平面的右侧， $y$ 轴通常指向成像平面的下方， $z$ 轴通常指向相机的光轴方向。

因此，第一个相机和第二个相机的坐标系通常是不同的，因为它们位于不同的位置、方向和距离上，因此需要使用不同的相机矩阵来表示它们的投影矩阵。

choose_solution.py

这段代码的作用是从一组旋转和平移矩阵 $Rt s$ 中选择一个最优解。这些矩阵用于将一个点从相机1的坐标系转换到相机2的坐标系。

具体地，这个函数计算每个旋转和平移矩阵 $R$ 和 $t$ 对应的相机1和相机2的投影矩阵 $P_1$ 和 $P_2$ ，并使用这些矩阵对一组匹配的图像点进行三角化，得到三维点云。然后，对于每个旋转和平移矩阵，计算哪些点在两个相机都能看到（即在两个相机前面），并计算它们的数量。最终选择能够看到最多点的旋转和平移矩阵作为最优解，并返回该矩阵。

函数的输入参数包括：

$uv 1$ ：一个 $n\times 2$ 的矩阵，表示第一张图像中的 $n$ 个匹配点的像素坐标。
$uv 2$ ：一个 $n\times 2$ 的矩阵，表示第二张图像中的 $n$ 个匹配点的像素坐标。
$K 1$ 和 $K 2$ ：分别表示相机1和相机2的内参矩阵。
$Rt s$ ：一个包含多个旋转和平移矩阵的列表。

函数的输出参数包括：

$R$ 和 $t$ ：被选择为最优解的旋转和平移矩阵。

eight_point.py

这段代码实现了从给定的图像点对中计算基础矩阵的过程。基础矩阵是一个 3x3 的矩阵，用于将图像1中的点映射到图像2中的极线。具体来说，基础矩阵可以用于计算两个图像上的点对之间的对极几何关系。

该函数使用的方法是标准化8点算法（normalized 8-point algorithm），该算法通过最小二乘法来估计基础矩阵。具体来说，它使用归一化坐标来构造一个 $\times 9$ 的矩阵 $A$ ，然后使用奇异值分解（SVD）来计算基础矩阵 $F$ 。然后，通过强制基础矩阵满足 $F^\top F = I$ 的条件来获得最终的基础矩阵。

函数 normalize_points 用于对输入的点进行归一化，使得它们的坐标具有零均值和单位方差。函数 closest_fundamental_matrix 用于计算最接近给定基础矩阵的基础矩阵，满足 Frobenius 范数最小。

第13行：计算 $\times 9$ 的矩阵 $A$ ，矩阵每一行都是两个点 $u_1, v_1)$ 和 $u_2, v_2)$ 通过 Kronecker product 生成的 $2\times 2$ 的矩阵 $\begin{bmatrix} u_1u_2 & u_1v_2 & u_1 & v_1u_2 & v_1v_2 & v_1 & u_2 & v_2 & 1 \end{bmatrix}$ ，这里是将一个矩阵分割成单个的部分（Kronecker product），然后每一行是对应的点生成的向量。
第17行：对 $A$ 进行 SVD，返回 $U, s, V T$ ，其中 $s$ 是奇异值的向量。
第19行：将 $V T$ 的最后一行向量作为 $F$ 的向量表示，并将其形状转换为 $3\times 3$ 的矩阵。
第21行：使用函数 closest_fundamental_matrix 将 $F$ 转换为最接近它的奇异值矩阵，该矩阵具有形式 $\begin{bmatrix} s_1 & 0 & 0 \\ 0 & s_2 & 0 \\ 0 & 0 & 0 \end{bmatrix}$ ，其中 $s_1$ 和 $s_2$ 是 $F$ 的奇异值。
第24行：使用 $T 1$ 和 $T 2$ 通过它们的转置来“去规范化” $F$ ，得到从像素坐标到基础矩阵的映射。最后返回 $F$ 。

epipolar_match.py

这段代码实现了对极线搜索，根据已知的基础矩阵 $F$ 和图像1中的点 $uv 1$ ，在图像2中找到与之对应的点 $uv 2$ 。

具体来说，该函数遍历所有的点 $uv 1$ ，计算出该点在图像2中的对极线，然后在该对极线上进行搜索，找到与该点最佳匹配的点。这里的“最佳匹配”是指在搜索过程中误差最小的点。

在搜索过程中，对于每个 $uv 1$ ，首先取出以该点为中心，宽度为 $2 w + 1$ 的方形窗口 $W 1$ 。然后，沿着该点的对极线，从左往右依次取出图像2中的窗口 $W 2$ ，计算 $W 1$ 和 $W 2$ 之间的绝对差，以此作为误差衡量标准，寻找误差最小的 $W 2$ ，然后将其对应的点 $u 2$ 作为该点在图像2中的匹配点 $uv 2$ 。