一、题目描述
RSA加密算法在网络安全世界中无处不在,它利用了极大整数因数分解的困难度,数据越大,安全系数越高。
给定一个32位正整数,请对其进行因数分解,找出是哪两个素数的乘积。
二、输入描述
一个正整数num
0 < num <= 2147483647
三、输出描述
如果成功找到,以单个空格分割,从小到大输出两个素数,分解失败,请输出-1 -1。
四、解题思路
- 读取输入的正整数num;
- 计算num的平方根n,取整数部分作为循环的终止条件;
- 初始化一个空字符串s用于存储找到的素数因子;
- 初始化一个布尔变量flag为false,用于标记是否找到满足条件的素数因子;
- 从2开始循环遍历到n:
- 如果num能被当前的循环变量i整除,说明i是num的一个因子。
- 检查i和num/i是否都是素数,如果是素数,则找到满足条件的素数因子。
- 更新flag为true,同时根据i和num/i的大小关系将它们拼接到字符串s中。
- 根据flag的值判断是否成功找到满足条件的素数因子:
- 如果flag为true,输出字符串s。
- 如果flag为false,输出"-1 -1"表示分解失败。
- 结束程序。
该算法通过从2开始逐个遍历到num的平方根n,判断是否存在两个素数因子的乘积等于num。对于每个循环变量i,通过检查i和num/i是否都是素数来确定是否满足条件。算法的时间复杂度主要取决于因数分解的步骤,通常为O(sqrt(num)),其中num为给定的32位正整数。
五、JavaScript算法源码
function calculate(num) {
// 计算num的平方根n,取整数部分作为循环的终止条件
const n = Math.floor(Math.sqrt(num));
// 找到的素数因子
let s = "";
// 是否找到满足条件的素数因子
let flag = false;
for (let i = 2; i <= n; i++) {
// 如果num能被当前的循环变量i整除,说明i是num的一个因子
if (num % i === 0) {
// 是否是素数
if (isPrime(i) && isPrime(num / i)) {
flag = true;
if (i < num / i) {
s = i + " " + (num / i);
} else {
s = num / i + " " + i;
}
}
}
}
if (flag) {
return s;
} else {
return "-1 -1";
}
}
/**
* 是否是素数
*/
function isPrime(a) {
const n = Math.floor(Math.sqrt(a));
for (let i = 2; i <= n; i++) {
if (a % i === 0) return false;
}
return true;
}
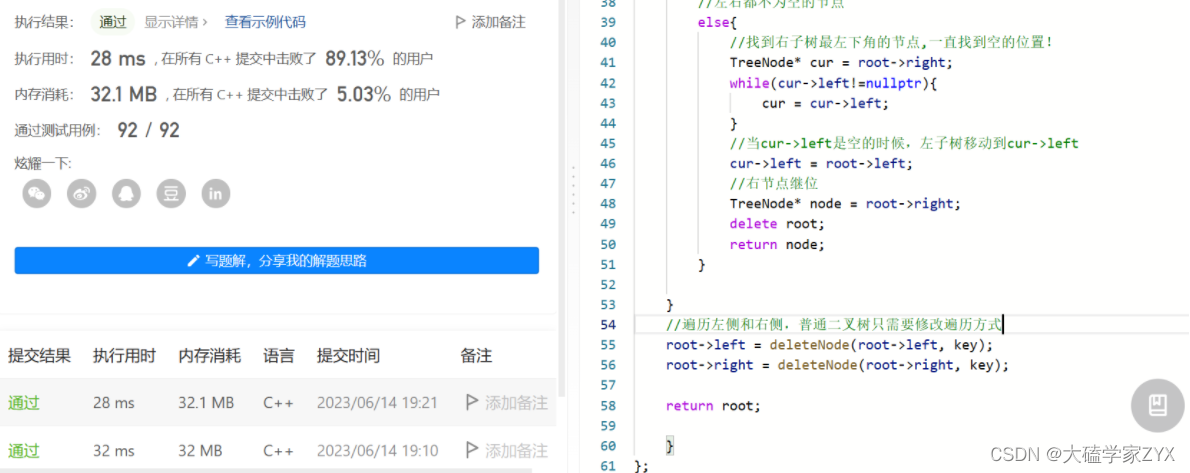
六、效果展示

🏆下一篇:华为OD机试真题 JavaScript 实现【相对开音节】【2022Q4 100分】,附详细解题思路
🏆本文收录于,华为OD机试(JavaScript)真题(A卷+B卷)
每一题都有详细的答题思路、详细的代码注释、样例测试,订阅后,专栏内的文章都可看,可加入华为OD刷题群(私信即可),发现新题目,随时更新,全天CSDN在线答疑。