封面图来源：
https://www.pexels.com/photo/aerial-shot-of-cargo-ship-on-sea-3840441/

作者：Hossein Abouee-Mehrizi, Oded Berman, Shrutivandana Sharma
引用：Abouee-Mehrizi, H., Berman, O., & Sharma, S. (2015). Optimal joint
replenishment and transshipment policies in a multi-period inventory
system with lost sales. Operations Research, 63(2), 342-350.
文章链接：https://doi.org/10.1287/opre.2015.1358

问题定义

文章考虑了包含两个零售商 (stocking locations) 的多期库存系统（有限规划期）；在每个时期，两个零售商可以选择从供应商或由另一个零售商的主动横向转运进行补充库存。文章构建随机控制问题，确定了最佳的补货和转运策略，使整体预期成本最小化。

(Paterson et al. 2011)库存系统的传统设计是分层次的，运输流从一个梯队到下一个梯队，即从制造商到批发商，从批发商到零售商等。更灵活的系统还允许在一个梯队内进行横向转运(lateral transhsipment)，即在同一梯队的批发商或零售商内部之间。通过这种方式，同一梯队的库存组成部分将库存集中起来，可使整体的库存水平和成本降低，同时仍达到所需的服务水平。考虑不同的转运时间点，横向转运的文献主要有两类：横向转运既可以限制在所有需求实现之前的预定时间进行(主动转运，proactive transshipment)，或在任何时间进行，以应对缺货或潜在的缺货 (被动转运，reactive transshipment).

联合补货 (joint replenishment): 库存控制中的联合补货指的是一种策略，即多种物品一起被重新订购，通常是为利用订购、运输和处理成本中的规模经济，在处理由同一供应商提供的或可以同时运输的多种物品时十分有效。在本文中，“联合”指的并非多种物品（文章只考虑单一物品 single-item)，而是补充货物的来源，其既可是一般意义上的供应商 (wareshouse) 也可是系统中的另一个库存地点。

模型构建

在有限的规划期内 ($t=1,2,\dots ,N$) ，库存系统中的两个库存地点 ($l=1,2$) 要满足非负随机需求$D_l^t$，且库存在最后一期结束后过期。对于每一个需求$D_l^t$，定义实际满足的需求$z_l^t$，以及概率密度函数$f_{D_1^t{D}_2^t}$和分布函数$F_{D_1^t{D}_2^t}$，且每期已知。在每一个时期开始时，

•每个库存地点可下订单从供应商处补货，订单数量 (order quantity) 定义为$y_l^t$

•每个库存地点亦可收到从另一库存位置发出的转运库存，定义为$x_l^t$

以上两个补货行为互相独立。转运库存在每个时期开始前已确定，且在满足需求前到达另一位置，因此，每个库存位置使用（若存在）上一时期所剩库存、收到的补货库存、收到的转运库存来满足需求。订单下达到送到的时间 (lead time) 忽略不计。

模型考虑的成本包括：

1. 单位订货成本 (unit ordering cost) $k_l^t$
2. 单位转运成本 (unit transshipment cost)$c_l^t$
3. 销售损失惩罚成本 (lost sale penalty cost)$p_l^t$
4. 持有成本 (holding cost)$h_l^t$
5. 过期成本 (expiration cost)$e_l$

1-4 严格为正，$e_l\in \mathbb{R}$.

文章对以上成本的数值关系进行假设，其中包括：

1. $k_1^t+c_1^t>k_2^t$, $k_2^t+c_2^t>k_1^t$, t ∈ { 1 , … , N } t\in\{1,\ldots,N\} t∈{1,…,N};

补货后再转运至另一库存地点成本比仅在另一地点补货成本高。

2. $p_1^t+c_1^t>p_2^t$, $p_2^t+c_2^t>p_1^t$, t ∈ { 1 , … , N } t\in\{1,\ldots,N\} t∈{1,…,N};

转运产品而失去自己的需求比不转运而让其他库存地点失去需求的惩罚要高。

3. $p_1^t>k_1^t$, $p_2^t>k_2^t$, t ∈ { 1 , … , N } t\in\{1,\ldots,N\} t∈{1,…,N};

对于每一个库存地点来说，失去需求的惩罚比补货高。

4. $h_1^t+p_1^t>p_1^{t+1}$, $h_2^t+p_2^t>p_2^{t+1}$, t ∈ { 1 , … , N − 1 } t\in\{1,\ldots,N-1\} t∈{1,…,N−1};

持有库存且在当期失去需求（即不满足），比不持有并在下期失去需求，成本更高。

5. $-e_1<p_1^N$, $-e_2<p_2^N$;

最后一期结束后，回收过期库存所得的收益小于销售损失的惩罚成本；即系统不鼓励在最后一期囤积库存。

6. $k_1^N>-e_1$, $k_2^N>-e_2$, $k_1^N+c_1^N>-e_2$, $k_2^N+c_2^N>-e_1$;

在最后一期，任何库存地点不为回收收益而补货或转运。

设每个库存地点在收到补货及转运后（即在满足需求前）的库存为$q_l^t:=s_l^t-x_l^t+x_{l^{\prime }}^t+y_l^t$，其中$s_l^t$为当期开始前的库存。令$b_l^{t+1}=q_l^t-z_l^t$，则 ( b l t + 1 ) − = max ⁡ { − b l t + 1 , 0 } (b_l^{t+1})^-=\max\{-b_l^{t+1},0\} (blt+1​)−=max{−blt+1​,0}为销售损失， ( b l t + 1 ) + = max ⁡ { b l t + 1 , 0 } (b_l^{t+1})^+=\max\{b_l^{t+1},0\} (blt+1​)+=max{blt+1​,0}为当期剩余库存，即$(b_l^{t+1}{)}^{+}=s_l^{t+1}$. 于是，规划期内的总需求可表示为

$$C:=\sum _{t=1}^N\sum _{l=1}^2[c_l^t{x}_l^t+k_l^t{y}_l^t+p_l^t(B_l^{t+1}{)}^{-}+h_l^t(B_l^{t+1}{)}^{+}]$$
$$+\sum _{l=1}^2[c_l^N{x}_l^N+k_l^N{y}_l^N+p_l^N(B_l^{N+1}{)}^{-}+e_l(B_l^{N+1}{)}^{+}]$$

其中 B l t + 1 = B l t + − x l t + x l ′ t + y l t − D l t , l ∈ { 1 , 2 } , l ′ = 3 − l , t ∈ { 1 , 2 , … , N } , B_l^{t+1}=B_l^{t+}-x_l^t+x_{l'}^t+y_l^t-D_l^t, l\in\{1,2\}, l'=3-l, t\in\{1,2,\ldots, N\}, Blt+1​=Blt+​−xlt​+xl′t​+ylt​−Dlt​,l∈{1,2},l′=3−l,t∈{1,2,…,N},
且 B l 1 + = S l , B l 1 − = 0 , l ∈ { 1 , 2 } , ( s 1 1 , s 2 1 ) = ( S 1 , S 2 ) ∈ R + 2 , ( S 1 , S 2 ) B_l^{1+}=S_l, B_l^{1-}=0, l\in\{1,2\}, (s_1^1, s_2^1) = (S_1,S_2)\in\mathbb{R}_+^2, (S_1,S_2) Bl1+​=Sl​,Bl1−​=0,l∈{1,2},(s11​,s21​)=(S1​,S2​)∈R+2​,(S1​,S2​)已知。

因此，该问题可表示为求解以下模型：

$\underset{(x_1^t,x_2^t,y_1^t,y_2^t{)}_{y=1}^N}{\min }$ $E_{(D_1^t,D_2^t{)}_{t=1}^N}[C]$

s.t. $0\le x_1^t\le (b_1^t{)}^{+}$,$0\le x_2^t\le (b_2^t{)}^{+}$,$y_1^t\ge 0$,$y_2^t\ge 0$, t ∈ { 1 , 2 , … , N } t\in\{1,2,\ldots,N\} t∈{1,2,…,N}

该模型约束表示，转运数量不可超过该地点现有库存；同时也可判断以下关于最优解的特征（原文引理1）：

若$({\hat{x}}_1^t,{\hat{x}}_2^t,{\hat{y}}_1^t,{\hat{y}}_2^t)$ t ∈ { 1 , 2 , … , N } t\in\{1,2,\ldots,N\} t∈{1,2,…,N}为以上模型的最优解，则对于每一时期，以下两条件必满足其中之一：（1）${\hat{x}}_1^t={\hat{x}}_2^t=0$，（2）${\hat{x}}_1^t=0$或${\hat{x}}_2^t=0$. （即两个库存位置的转运数量至少有一个为零。）

最优策略

文章通过动态规划和数学归纳法对最优解的特征进行归纳及证明，详情请见原文第三节（3.1前与3.2）；进一步地，文章对最优解的空间进行定义。令${\mathcal{F}}_{ijk}^t$表示在$t$时段的一组最优联合补货策略，其中 i ∈ { 0 , + , − } i\in\{0,+,-\} i∈{0,+,−}分别表示零转运，从位置1至2转运，从位置2至1转运，j, k ∈ { 0 , + } k\in\{0,+\} k∈{0,+}分别表示零补货（从供应商）和订单数量为正（二者具体数值稍后解释）。比如，${\mathcal{F}}_{-+0}^t$表示，对于起始库存${\mathcal{F}}_{-+0}^t$有最优策略${\hat{x}}^t<0$（即从位置2运至1），${\hat{y}}_1^t>0,{\widehat{y_2}}^t=0$（位置1补货，位置2不补货）。

图1描述了对于不同起始库存的最优策略（尚不包括数量），同时也给出了上述曲线的交点以及两两区域分割线与坐标轴的位置关系，虚线表示为相邻的分割线上对应的最优策略不包含在虚线所在的区域。图1中曲线$I_{x^t}^c(c_2^t)$,$I_{x^t}^c(-c_1^t)$,$I_{y_1^t}^c(-k_1^t)$,$I_{y_2^t}^c(-k_2^t)$分别由下式给出，其中$I_{x^t}$表示转运输量（1至2）对最优的未来成本期望的增长率（详见原文公式6），$I_{y_l^t}$同理。

$I_{x^t}(b_1^{t+},b_2^{t+},0,0,0)=c_2^t$,
$I_{x^t}(b_1^{t+},b_2^{t+},0,0,0)=-c_1^t$,
$I_{y_1^t}(b_1^{t+},b_2^{t+},0,0,0)=-k_1^t$,
$I_{y_2^t}(b_1^{t+},b_2^{t+},0,0,0)=-k_2^t$.

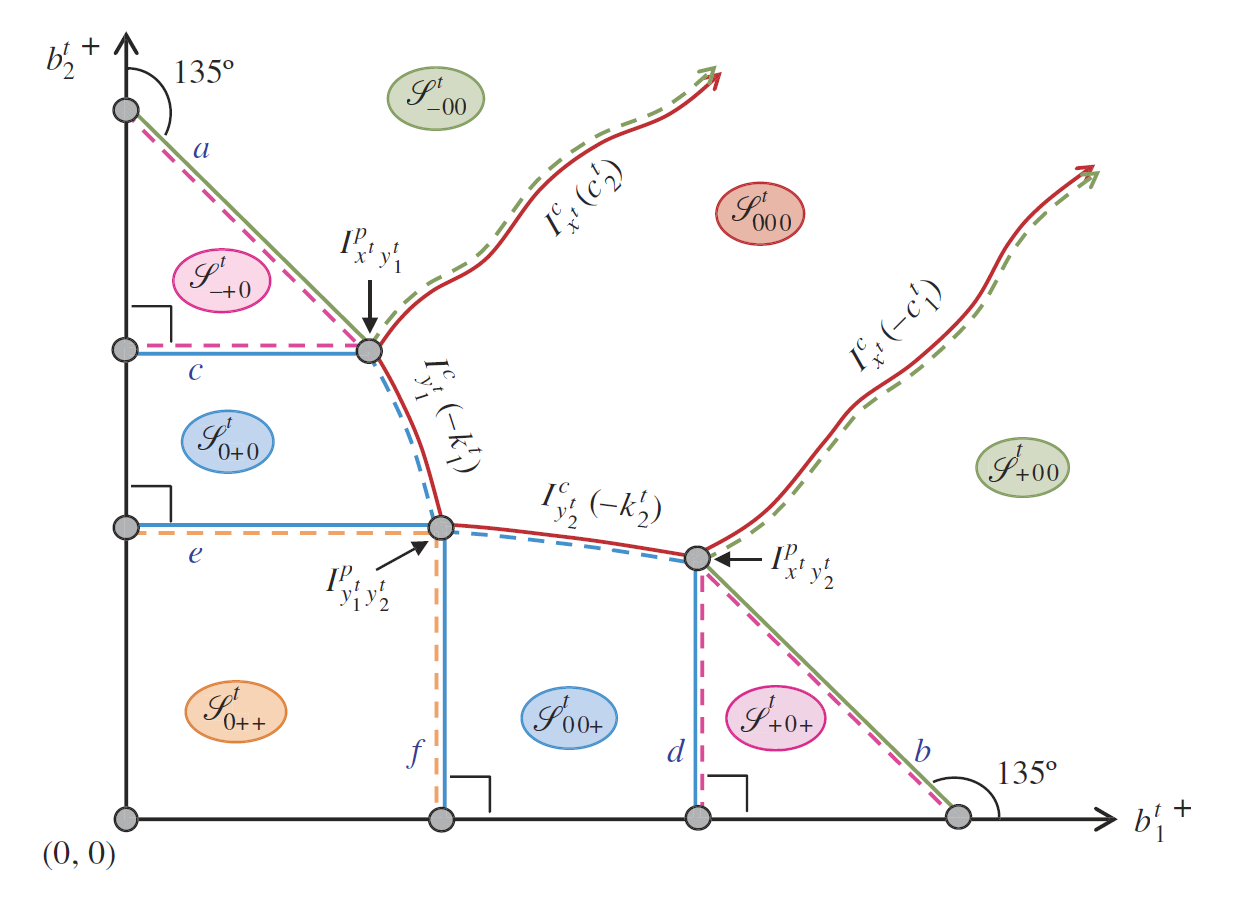
图1：不同起始库存状态对应的最优联合补货策略（尚不包括数量）图片来源：Abouee-Mehrizi et al. (2015)

请注意，$I_{y_1^t{y}_2^t}^p$并非一定位于第一象限；基于库存系统给定的各单位成本，其有可能落在第二或第四象限。类似地,$I_{y_1^t{y}_2^t}^p$与$I_{x^t{y}_2^t}^p$同样有可能分别落于第二、四象限。若以上三点处于第一象限外，则图1中的某些区域可能不存在，这说明相应的解对于这一单位成本组合并非最优。

图2详细地给出了对于不同起始库存状态的最优联合补货策略。比如，对于任意对应${\mathcal{F}}_{-00}^t$的起始状态(${\mathcal{F}}_{-00}^t$), 地点2所持有的库存足够多，可通过转运来减轻自身的持有成本，且同时可以满足另一地点的需求，转运数量为${\hat{x}}^t$，即需将原有的$(b_1^{t+},b_2^{t+})$某点位于曲线$I_{x^t}^c(c_2^t)$上，且位移夹角为45度。再比如，对于两地点起始库存均不高的情况，其对应的最优策略由${\mathcal{F}}_{0++}^t$表示，即两地点所持有库存均不足以进行转运而使成本最小化，最优策略为对两地点从供应商处补货，数量为${\hat{y}}_1^t,{\hat{y}}_2^t$, 路径与位移夹角（90度）如图1所示。

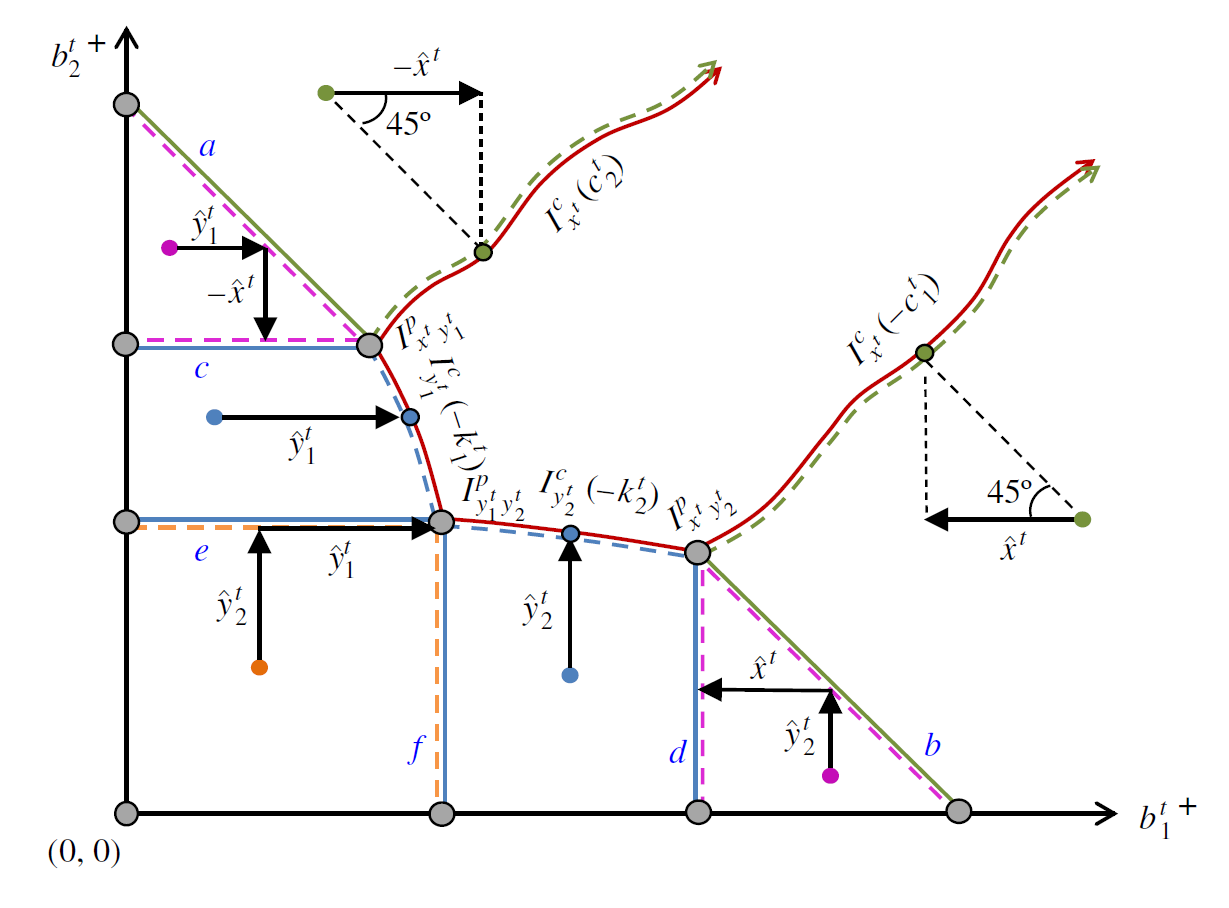
图2：不同起始库存状态对应的最优联合补货策略（包括数量，如箭头所示）图片来源：Abouee-Mehrizi et al. (2015)

基于图1与图2，若起始库存$(b_1^{t+},b_2^{t+})$属于${\mathcal{F}}_{000}^t$，则转运与补货均不需要进行；而对于起始库存属于${\mathcal{F}}_{000}^t$之外的情况，库存水平将被通过转运或补货（或兼而有之）提升至$I_{x^t}^c(-c_1^t)$,$I_{x^t}^c(c_2^t)$,$I_{y_1^t}^c(-k_1^t)$,$I_{y_1^t}^c(-k_1^t)$曲线上的某一点，或其两两间的交点$I_{y_1^t{y}_2^t}^p$,$I_{x^t{y}_1^t}^p$,$I_{x^t{y}_2^t}^p$.

因此，由上述曲线所形成的${\mathcal{F}}_{000}^t$区域的边界，可被理解为$t$时段的“订货至”曲线 (order-up-to curves，$OO{C}^t$)，其上的点是$t$
时段基于给定起始库存$(b_1^{t+},b_2^{t+})$的最优转运、订货策略。

同时，任一起始库存$(b_1^{t+},b_2^{t+})$（除${\mathcal{F}}_{000}^t$内）所对应$OO{C}^t$上的点唯一，所以所述最优策略是依赖状态的 (state-dependent policy).

此处可参见 Agrawal et al. (2004) ，其提出主动转运最优策略对起始状态的依赖性。

除一般的转运与补货，文章通过设定足够大的转运或补货成本，使对应的库存行为不被包含在最优解中。图3与图4分别表示了两种情况下的最优策略。

•图3中，设定$c_1^t,c_2^t\gg 0$,则原最优策略中的$I_{x^t}^c(-c_1^t)$、$I_{x^t}^c(c_2^t)$则将分别向右下和左上移动，直至消失在第一象限。

•图4中，设定$k_1^t,k_2^t\gg 0$，则原最优策略中的补货区域全部消失，$I_{y_1^t}^c(-k_1^t)$、$I_{y_2^t}^c(-k_2^t)$则均将向左下移动，直至消失在第一次象限。

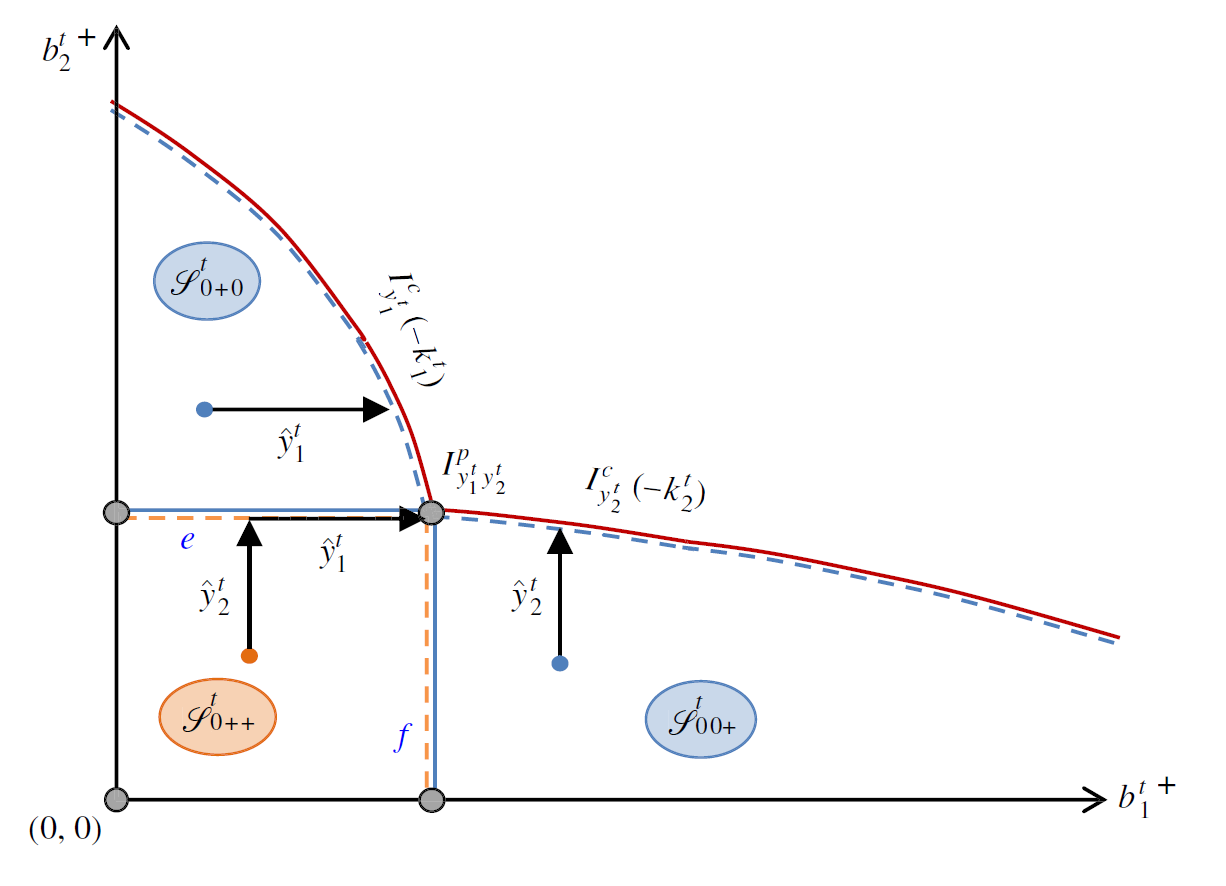
图3：不考虑转运（仅补货）的最优策略 图片来源：Abouee-Mehrizi et al. (2015)

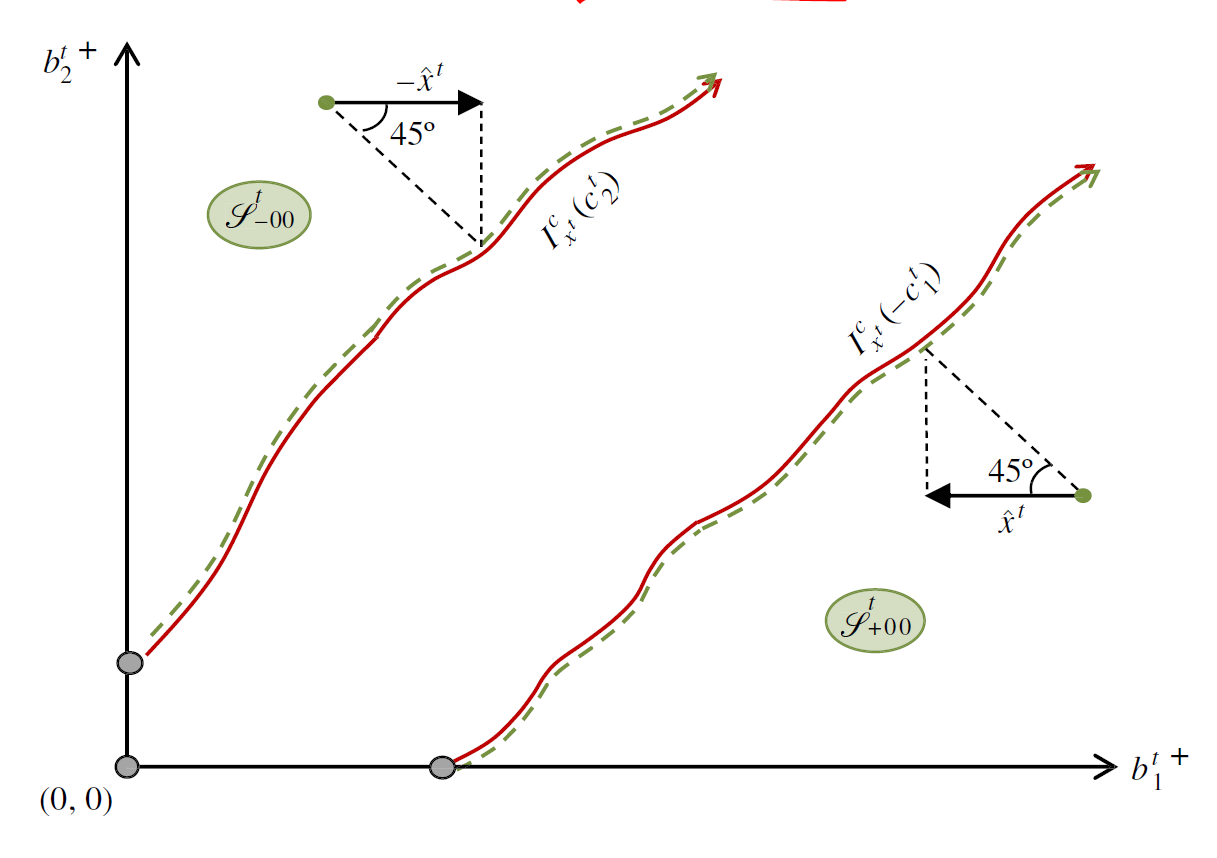
图4: 不考虑补货（仅转运）的最优策略 图片来源：Abouee-Mehrizi et al. (2015)

参考文献

Abouee-Mehrizi, H., Berman, O., & Sharma, S. (2015). Optimal joint replenishment and transshipment policies in a multi-period inventory system with lost sales. Operations Research, 63(2), 342-350.

Agrawal, V., Chao, X., & Seshadri, S. (2004). Dynamic balancing of inventory in supply chains. European Journal of Operational Research, 159(2), 296-317.

Paterson, C., Kiesmüller, G., Teunter, R., & Glazebrook, K. (2011). Inventory models with lateral transshipments: A review. European Journal of Operational Research, 210(2), 125-136.