小论文有两个部分组成，第一个是用电路仿真实现信号的调制与解调，第二个是通过python将DFT和FFT运算的次数可视化。

信号调制与解调

在本学期信号与系统课程上，当老师讲到信号的调制与解调部分时，脑子里没有一个直观的印象，导致那部分学的很模糊，而后再模拟电子技术基础课上，学了模拟乘法器之后，想尝试通过乘法器实现调制，而后通过滤波实现解调，最终在考试复习的时候才对信号的调制与解调有了较深入了解。

因此我打算使用NI Multisim软件通过仿真电路实现信号调制与解调。

模拟乘法器AD734

AD734是一个集成模拟乘法器，具有高精度，宽频带的特点。

根据datasheet可知，该乘法器最基本的方程为：
$$W=A_o\frac{(X_1-X_2)(Y_1-Y_2)}{U}-(Z_1-Z_2)(1)$$

其中Ao为输出级的开环放大倍数，AD734的为72dB和MOPY634的为85dB;

U为比例因子，激光调整至 10V，但使用外部电阻器可调在 3V 至 10V 范围内。

当提供负反馈路径时，电路使得括号内的数量基本上为零，会使得以下方程成立：
$$(X_1-X_2)(Y_1-Y_2)=U(Z_1-Z_2)(2)$$
此外在使用该电路实现运算时，将Z1与W连接在一起，从而：
$$V_{out}=\frac{(X_1-X_2)(Y_1-Y_2)}{U}+Z_2(3)$$

在本次实验中，X2,Y2,Z2接地处理，完成电路搭建如图所示：

上边XFG为信号发生器，XFG1产生50Hz、幅度为1的正弦波，XFG2产生1000Hz、幅度为1的正弦波，

信号调制

$y(t)=0.1f(t)\cdot C(t)$，其中0.1为乘法因子。

$f(t)=sin(\Omega t)$， $C(t)=sin(w_{c}t)$，$w_c>>\Omega$

$f(t)$为50Hz、幅度为1的正弦波，调制信号$C(t)$为1000Hz、幅度为1的正弦波。

通过乘法器后，如下所示：

可以看出，正弦波信号对三角波信号进行了载波调制。

信号解调

为了从该信号中得出原信号（三角波信号），采用同步解调的方法，对该信号再乘上$sin(w_{c}t)$，而后通过低通滤波器电路。

$y(t)=0.1f(t)\cdot C(t)\cdot 0.1sin(w_{c}t)，w_c=2000\pi$

同样使用AD734模拟乘法器实现乘法，而后用二阶低通滤波器进行解调，电路搭建如下：

输出波形如下：

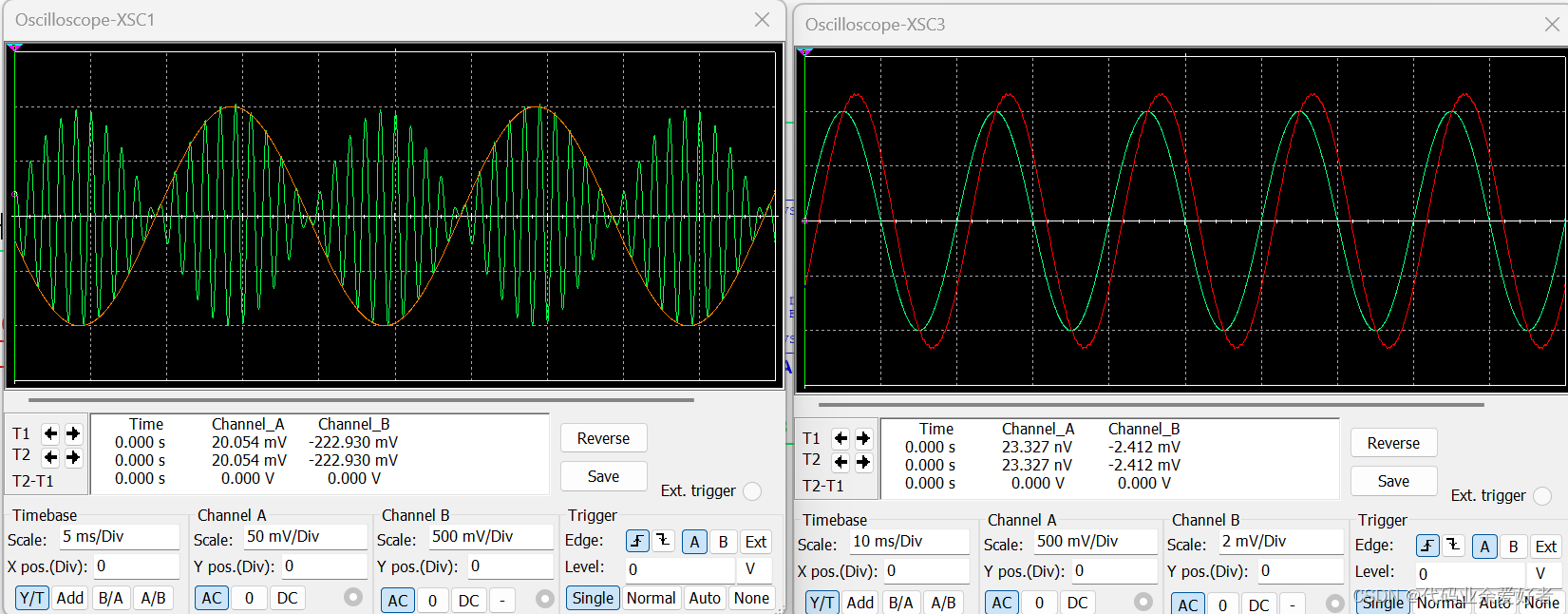
左图为原信号与正弦调制信号，右图为原信号与解调后的信号。

通过输出波形得知，解调后的正弦波信号出现相移和幅度损失，频率为50Hz，幅度为4.5mA。

通过理论计算，两次乘法中0.01的乘法因子，通过同步解调，会将幅度变成原来的0.5倍。因此理论上，输出为1
$V_{out}=0.1\ast 0.1\ast 0.5\ast 1=5mA$。通过电路分析，可能是由于低通滤波特性好不够好，或者模拟乘法器内部误差导致的，但是总体误差还可以接受。

DFT和FFT 的运算复杂度比较

DFT运算

x(n)是一个长为M的序列，其离散傅里叶变换（DFT）为：

公式： $X(k)=DFT[x(n)]={\sum }_{n=0}^{N-1}x(n)e^{-j\frac{2\pi }{N}kn},k=0,1,\mathrm{2....},N-1$

离散傅里叶逆变换为：

公式: $x(n)=IDFT[X(k)]=\frac{1}{N}{\sum }_{n=0}^{N-1}X(k)e^{j\frac{2\pi }{N}kn},k=0,1,\mathrm{2....},N-1$

从公式可以看出时间离散信号的DFT得到的是离散的频域信号！

复数乘法：$N^2$
复数加法：$N(N-1)$

FFT运算

快速傅里叶变换通常采用基2时间抽取FFT算法，采用蝶形运算对复数信号进行运算时，每一次需要一次复数乘法和二次复数加法，当$N=2^M$时，分解级数为M级，每一级有$N/2$个蝶形。

复数乘法：$\frac{N}{2}\times M=\frac{N}{2}{\log }_{2}N$
复数加法：$\frac{N}{2}\times 2\times M=N{\log }_{2}N$

复杂度比较

为了更具象的了解DFT和FFT算法的复杂度，将两者的复杂度做一比较，代码如下：

import numpy as np
import matplotlib.pyplot as plt
import time
from matplotlib.animation import FuncAnimation

def dft(x):
    N = len(x)
    n = np.arange(N)
    k = n.reshape((N, 1))
    e = np.exp(-2j * np.pi * k * n / N)
    X = np.dot(e, x)
    mult = N**2  # Multiplication count
    add = N*(N-1)  # Addition count
    return X, mult, add

def fft(x):
    N = len(x)
    if N <= 1:
        return x, 0, 0
    even, even_mult, even_add = fft(x[::2])
    odd, odd_mult, odd_add = fft(x[1::2])
    factor = np.exp(-2j * np.pi * np.arange(N) / N)
    factor_odd = factor[:N//2] * odd
    factor_even = factor[N//2:] * even
    mult = even_mult + odd_mult + N*2
    add = even_add + odd_add + N*3
    return np.concatenate([factor_even + factor_odd, factor_even - factor_odd]), mult, add

# Initialize variables
N_max = 500
N_values = np.arange(2, N_max + 1,1)
dft_mults = []
dft_adds = []
fft_mults = []
fft_adds = []

# Calculate multiplication and addition counts for each data length
for N in N_values:
    x = np.random.random(N)

    # Calculate DFT multiplication and addition counts
    _, dft_mult, dft_add = dft(x)
    dft_mults.append(dft_mult)
    dft_adds.append(dft_add)

    # Calculate FFT multiplication and addition counts
    _, fft_mult, fft_add = fft(np.pad(x, (0, 2**int(np.ceil(np.log2(N))) - N), 'constant'))
    fft_mults.append(fft_mult)
    fft_adds.append(fft_add)

# Initialize figure and axis
fig, ax = plt.subplots()
ax.set_xlim(0, N_max +1)
ax.set_ylim(0, max(max(dft_mults), max(fft_mults), max(dft_adds), max(fft_adds)) + 100)
line_dft_mult, = ax.plot([], [], 'bo-', label='DFT Multiplication')
line_dft_add, = ax.plot([], [], 'cs-', label='DFT Addition')
line_fft_mult, = ax.plot([], [], 'ro-', label='FFT Multiplication')
line_fft_add, = ax.plot([], [], 'mo-', label='FFT Addition')
ax.set_xlabel('Data Length (N)')
ax.set_ylabel('Operation Count')
ax.set_title('DFT vs FFT Complexity Comparison')
ax.legend()
ax.grid(True)

# Update function for animation
def update(frame):
    n = frame + 2
    ax.set_title(f'DFT vs FFT Complexity Comparison (N = {n})')
    line_dft_mult.set_data(N_values[:frame+1], dft_mults[:frame+1])
    line_dft_add.set_data(N_values[:frame+1], dft_adds[:frame+1])
    line_fft_mult.set_data(N_values[:frame+1], fft_mults[:frame+1])
    line_fft_add.set_data(N_values[:frame+1], fft_adds[:frame+1])
    return line_dft_mult, line_dft_add, line_fft_mult, line_fft_add

# Create animation
ani = FuncAnimation(fig, update, frames=N_max - 1, interval=200, repeat=False)

# Show the animation
plt.show()

由于FFT运算需要进行补零扩充到2的M次幂，所以某一区间内的FFT运算次数是一样的，从上图可以看出随着序列长度的不断增加，两者的运算次数出现了显著的区别。

但是对卷积进行FFT运算时，假如两个序列长度相差巨大，或者两个长度均较小时，使用FFT反而会使运算更加复杂。

只有当两个序列长度很长，且相差不大时，使用FFT运算将会非常显著地提高运算速度。