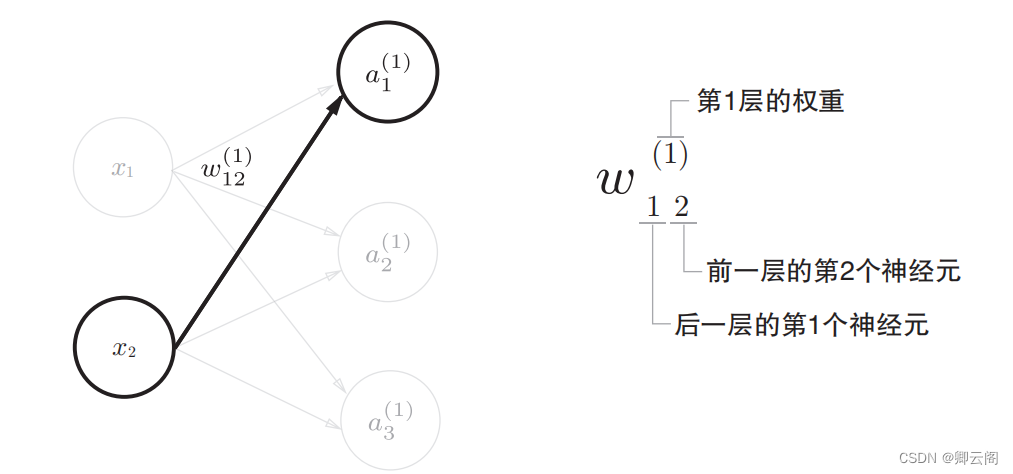
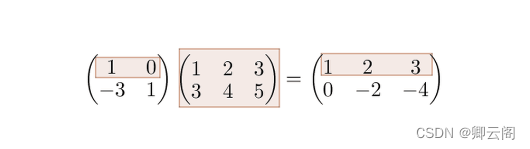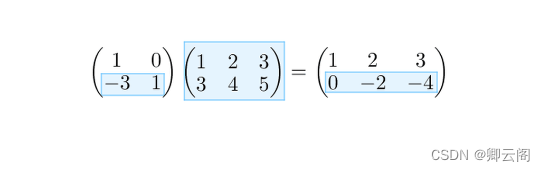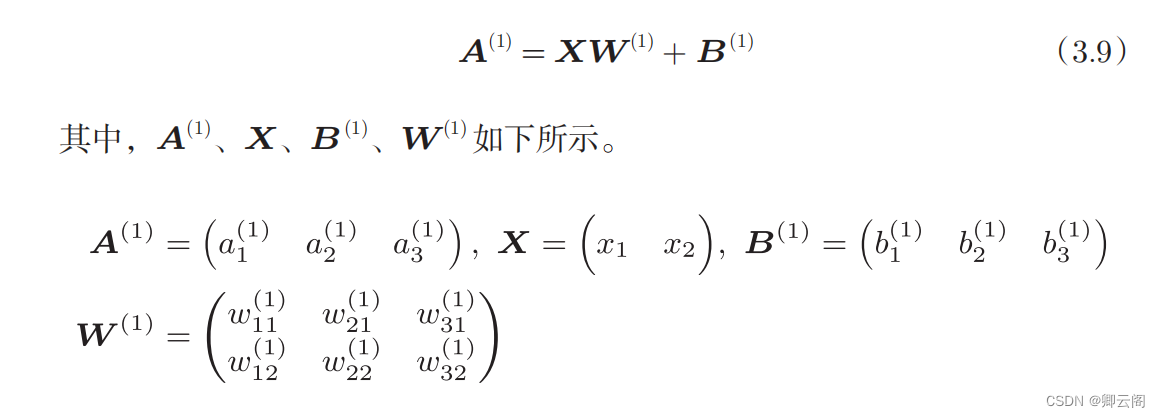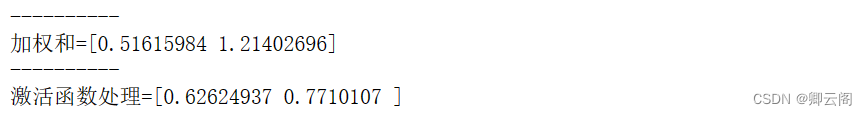🌞欢迎来到深度学习的世界
🌈博客主页:卿云阁💌欢迎关注🎉点赞👍收藏⭐️留言📝
🌟本文由卿云阁原创!
🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢!
目录
3.1 从感知机到神经网络
3.2 激活函数
3.3 多维数组的运算
3.4 3层神经网络的实现
3.5 输出层的设计
3.6 手写数字识别
CPU和GPU
对于机器学习和深度学习来说,GPU显然更适合一点。两者的区别可以这么理解,CPU相当于5-6个大学教授,GPU相当于100个高中生,显然如果我们只是单纯的想做1000到简单的数学题的话,使用GPU显然更合适。
3.1 从感知机到神经网络
3.1.1 神经网络的例子第 0 层对应输入层,第 1 层对应中间层,第 2 层对应输出层。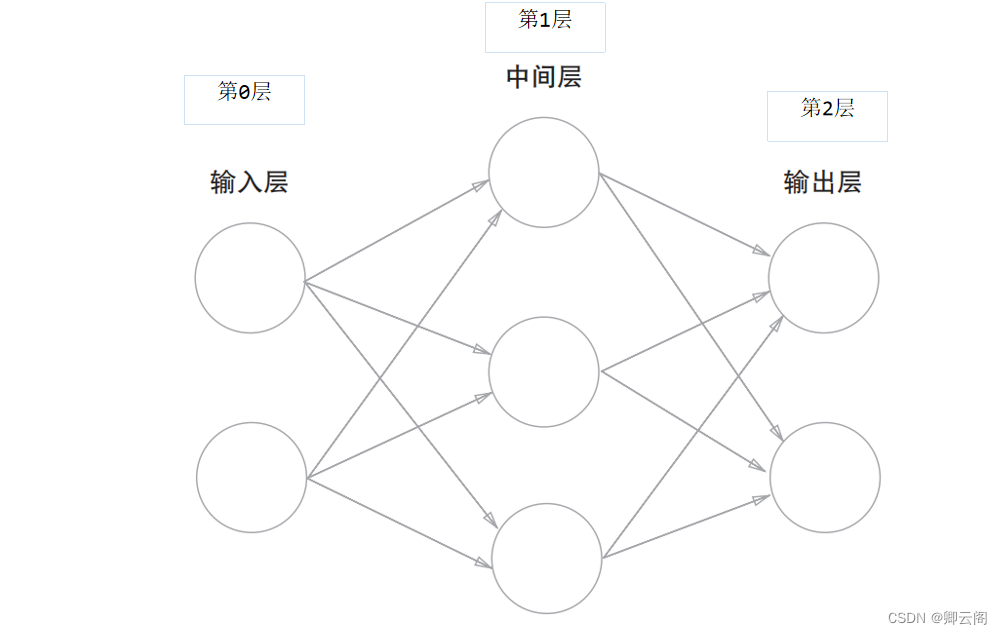
3.1.2 复习感知机
3.1.3 激活函数登场神经网络之所以要引入激活函数,主要是为了增加模型的非线性表达能力。 h(x )函数会将输入信号的总和转换为输出信号,这种函数 一般称为激活函数 ( activationfunction )。如“激活”一词所示,激活函数的作用在于决定如何来激活输入信号的总和。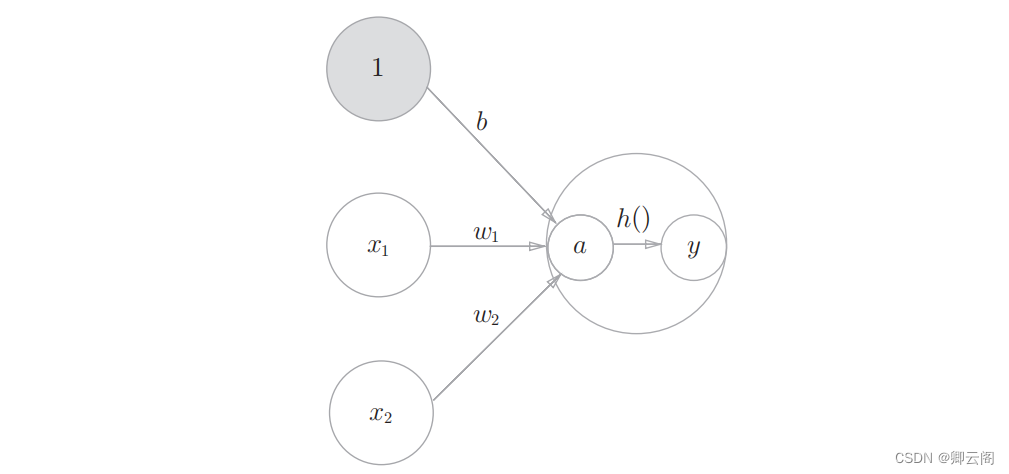
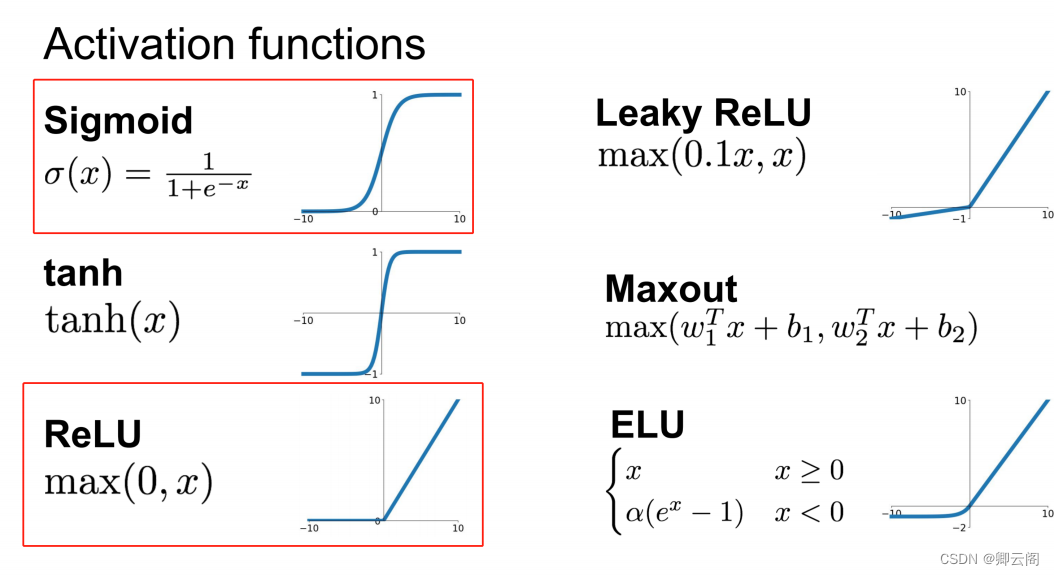
3.2 激活函数
3.2.1 sigmoid函数
3.2.2 阶跃函数的实现
当输入超过 0 时,输出 1 ,否则输出0 。可以像下面这样简单地实现阶跃函数。def step_function(x): if x > 0: return 1 else: return 0 print("h(a)={0}".format(step_function(3.0))) 结果: h(a)=1 但不允许参数取NumPy数组,例如step_function(np.array([1.0, 2.0]))。为了便于后面的操作,我们把它修 改为支持NumPy数组的实现。为此,可以考虑下述实现。支持NumPy数组的实现
前期准备
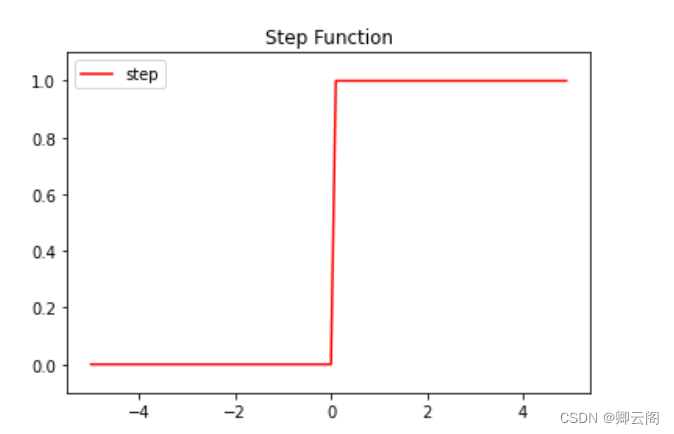
import numpy as np x = np.array([-1.0, 1.0, 2.0]) print("x={0}".format(x)) y = x > 0 print("----------") print("y={0}".format(y)) print("----------") y = y.astype(np.int) print("转化之后的y={0}".format(y))对NumPy 数组进行不等号运算后,数组的各个元素都会进行不等号运算, 生成一个布尔型数组。这里,数组x 中大于 0 的元素被转换为 True ,小于等 于0 的元素被转换为 False ,从而生成一个新的数组 y 。 数组y是一个布尔型数组,但是我们想要的阶跃函数是会输出 int 型的0或1 的函数。因此,需要把数组 y 的元素类型从布尔型转换为 int型。3.2.3 阶跃函数的图形np.arange(-5.0, 5.0, 0.1) 在 − 5 . 0 到 5 . 0 的范围内,以 0 . 1 为单位,生成 NumPy数组。import numpy as np import matplotlib.pylab as plt def step_function(x): return np.array(x > 0, dtype=np.int) x = np.arange(-5.0, 5.0, 0.1) y = step_function(x) print("y={0}".format(y)) plt.plot(x, y,color='red',label="step") plt.legend(loc='best') plt.title("Step Function") plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
3.2.4 sigmoid函数的实现
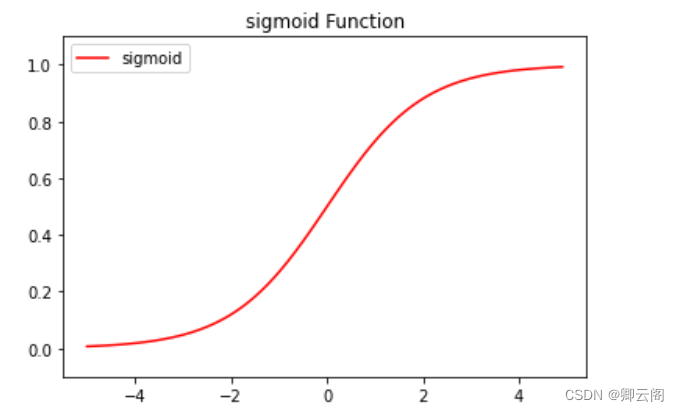
def sigmoid(x): return 1 / (1 + np.exp(-x)) x = np.array([-1.0, 1.0, 2.0]) y = sigmoid(x) print("----------") print("y=sigmoid(x)={0}".format(y)) #结果: #之所以sigmoid函数的实现能支持NumPy数组之所以 sigmoid 函数的实现能支持 NumPy 数组,根据NumPy 的广播功能,如果在标量和 NumPy 数组 之间进行运算,则标量会和NumPy 数组的各个元素进行运算。这里来看一个具体的例子。t = np.array([1.0, 2.0, 3.0]) print("----------") print("1.0 + t={0}".format(1.0 + t)) print("----------") print("1.0 / t={0}".format(1.0 / t)) #结果 #---------- #1.0 + t=[2. 3. 4.] #---------- #1.0 / t=[1. 0.5 0.33333333]def sigmoid(x): return 1 / (1 + np.exp(-x)) x = np.arange(-5.0, 5.0, 0.1) y = sigmoid(x) plt.plot(x, y,color='red',label="sigmoid") plt.legend(loc='best') plt.title("sigmoid Function") plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
3.2.5 sigmoid函数和阶跃函数的比较
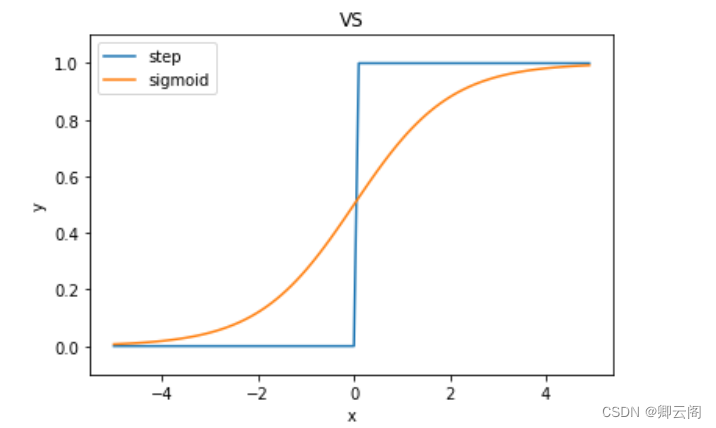
import numpy as np import matplotlib.pylab as plt #阶跃函数 def step_function(x): return np.array(x > 0, dtype=np.int) #sigmoid函数 def sigmoid(x): return 1 / (1 + np.exp(-x)) x = np.arange(-5.0,5.0,0.1) y1 = step_function(x) y2=sigmoid(x) plt.xlabel("x") plt.ylabel("y") plt.plot(x, y1,label="step") plt.plot(x,y2,label="sigmoid") plt.legend(loc='best') plt.title("VS") plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
- 首先注意到的是“平滑性”的不同。sigmoid函数是一条平 滑的曲线,输出随着输入发生连续性的变化。而阶跃函数以0为界,输出发生急剧性的变化。
- 相对于阶跃函数只能返回0或1,sigmoid函数可以返 回0.731 ...、0.880 ...等实数(这一点和刚才的平滑性有关)。也就是说,感知机中神经元之间流动的是0或1的二元信号,而神经网络中流动的是连续 的实数值信号。
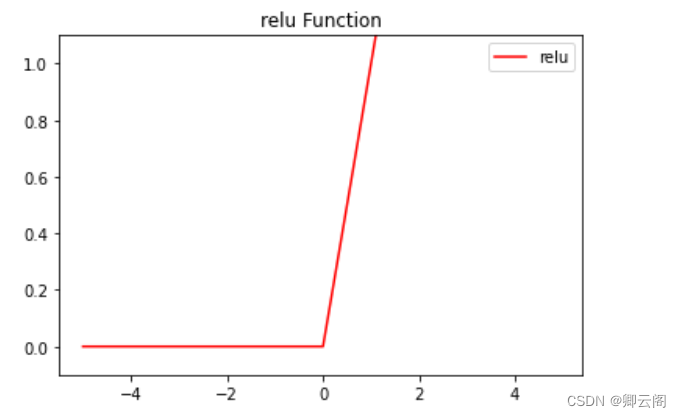
3.2.6 非线性函数阶跃函数和 sigmoid 函数还有其他共同点,就是两者均为 非线性函数。 sigmoid函数是一条曲线,阶跃函数是一条像阶梯一样的折线,两者都属于 非线性的函数。 神经网络的激活函数必须使用非线性函数。换句话说,激活函数不能使 用线性函数。为什么不能使用线性函数呢?因为使用线性函数的话,加深神 经网络的层数就没有意义了。3.2.7 ReLU函数ReLU 函数在输入大于 0 时,直接输出该值;在输入小于等于 0 时,输出0。 这里使用了 NumPy 的 maximum 函数。 maximum 函数会从输入的数值中选 择较大的那个值进行输出。
import numpy as np import matplotlib.pylab as plt def relu(x): return np.maximum(0, x) x = np.arange(-5.0, 5.0, 0.1) y = relu(x) plt.plot(x, y,color='red',label="relu") plt.legend(loc='best') plt.title("relu Function") plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
除了上面介绍的解阶跃函数,在深度学习领域还存在着着很多其它的激活函数。比如tanh函数,sigmoid函数,ReLu,Leaky ReLu以及softmax函数等等。
3.3 多维数组的运算
3.3.1 多维数组
import numpy as np A = np.array([1, 2, 3, 4]) print("----------") print("A={0}".format(A)) print("----------") print("A的维度={0}".format(np.ndim(A))) print("----------") print("A的形状={0}".format((A.shape))) print("----------") print("A的第一个元素={0}".format((A[0])))
#多维数组 import numpy as np B = np.array([[1,2], [3,4], [5,6]]) print("----------") print("B={0}".format(B)) print("----------") print("B的维度={0}".format(np.ndim(B))) print("----------") print("B的形状={0}".format((B.shape))) print("----------") print("B的第一个元素={0}".format((B[0][0])))3.3.2 矩阵乘法
#3.3.2 矩阵乘法 A = np.array([[1,0], [-3,1]]) B = np.array([[1,2,3], [4,5,6]]) print("----------") print("A*B={0}".format(np.dot(A, B))) #结果: #---------- #A*B=[[ 1 2 3] #[ 1 -1 -3]]
3.3.3 神经网络的内积
简单神经网络为对象。这个神经网络省略了偏置和激活函数,只有权重。.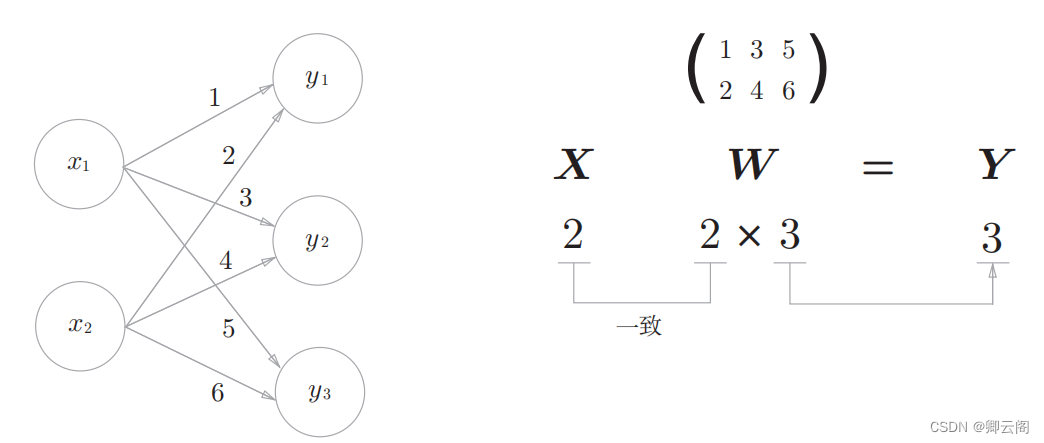
# 3.3.3 神经网络的内积 X = np.array([1, 2]) W = np.array([[1, 3, 5], [2, 4, 6]]) Y = np.dot(X, W) print("----------") print("X*W={0}".format(Y)) #结果: #---------- #X*W=[ 5 11 17]
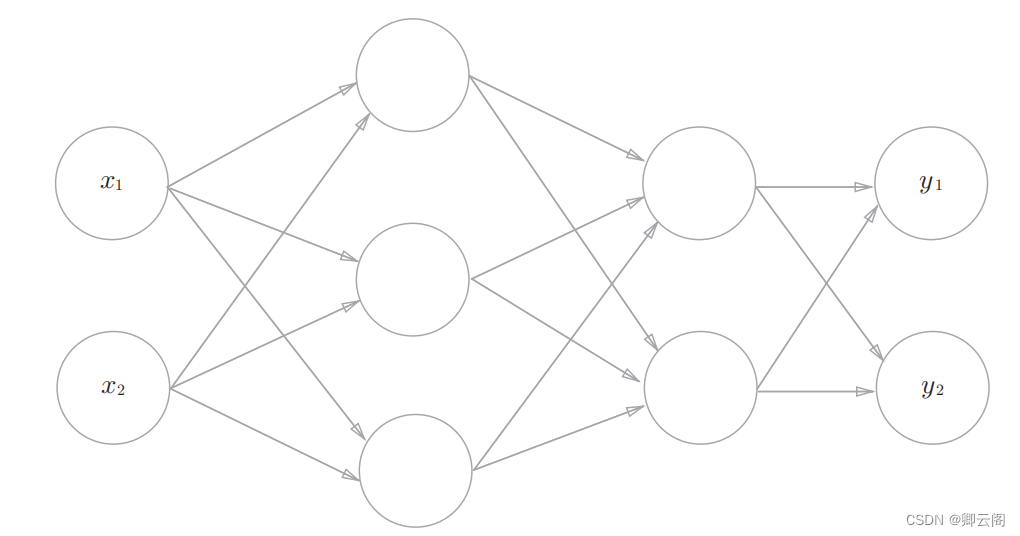
3.4 3层神经网络的实现
3.4.1 符号确认
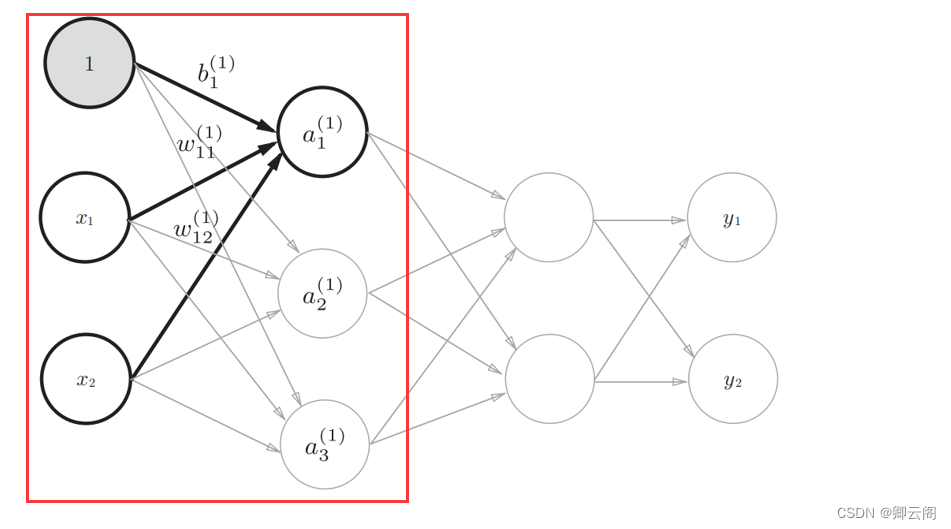
3.4.2 各层间信号传递的实现
下一层第一个神经元的输出
X是1*n的一个矩阵,n是该层神经元的个数。
W是权重矩阵,(n*m) n表示该层神经元的个数,m表示下一层神经元的个数。
b是偏置项,是1*m的一个矩阵 与下一层神经元的个数有关。
从输入层到第1层的信号传递
#从输入层到第1层的信号传递 X = np.array([1.0, 0.5]) W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) B1 = np.array([0.1, 0.2, 0.3]) A1 = np.dot(X, W1) + B1 Z1 = sigmoid(A1) print("----------") print("加权和={0}".format(A1)) print("----------") print("激活函数处理={0}".format(Z1))
从第1层到第2层的信号传递
#从第1层到第2层的信号传递 W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) B2 = np.array([0.1, 0.2]) A2 = np.dot(Z1, W2) + B2 Z2 = sigmoid(A2) print("----------") print("加权和={0}".format(A2)) print("----------") print("激活函数处理={0}".format(Z2))
从第2层到第3层的信号传递
#从第2层到第3层的信号传递 def identity_function(x): return x W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) B3 = np.array([0.1, 0.2]) A3 = np.dot(Z2, W3) + B3 Y = identity_function(A3) # 或者Y = A3 print("----------") print("加权和={0}".format(A3)) print("----------") print("激活函数处理={0}".format(Y))
3.4.3 代码实现小结
这里定义了 init_network() 和 forward() 函数。 init_network() 函数会进行权重和偏置的初始化,并将它们保存在字典变量network 中。这个字典变量network 中保存了每一层所需的参数(权重和偏置)。 forward()函数中则封装了将输入信号转换为输出信号的处理过程。import numpy as np #定义激活函数 def sigmod(x): return 1 / (1 + np.exp(-x)) def indentify_function(x): return x # 在本程序中使用numpy来实现一个简单的神经网络 # 定义好神经网络的初始化函数 def init_network(): network = {} network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) network['B1'] = np.array([0.1, 0.2, 0.3]) network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) network['B2'] = np.array([0.1, 0.2]) network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]]) network['B3'] = np.array([0.1, 0.2]) return network def forward(network, x): W1 = network['W1'] W2 = network['W2'] W3 = network['W3'] B1 = network['B1'] B2 = network['B2'] B3 = network['B3'] a1 = np.dot(x, W1) + B1 z1 = sigmod(a1) a2 = np.dot(z1, W2) + B2 z2 = sigmod(a2) a3 = np.dot(z2, W3) + B3 y = indentify_function(a3) return y # 开始运行神经网络 network = init_network() x = np.array([1, 2]) y = forward(network, x=x) print("---最后的输出---") print(y) #结果: #---最后的输出--- #[0.32403126 0.71230655]3.5 输出层的设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。一般而言,回归问题用恒等函数,分类问题用softmax 函数。3.5.1 恒等函数和 softmax函数分类问题中使用的 softmax函数, 设输出层共有 n 个神经元,计算第 k 个神经元的输出。如
softmax 函数的分子是输入信号的指数函数,分母是所有输入信号的指数函数的和。
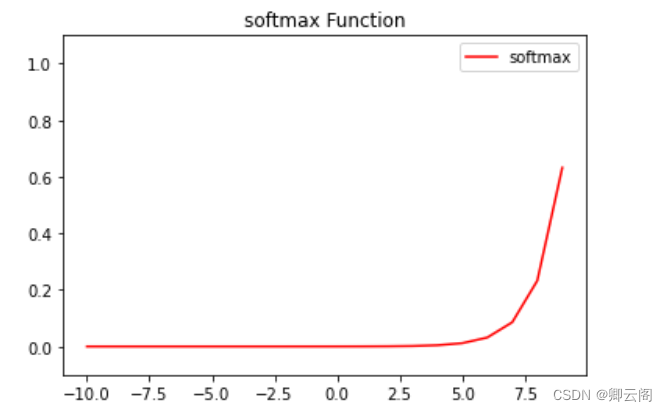
#softmax函数 import numpy as np import matplotlib.pylab as plt def softmax(a): exp_a = np.exp(a) sum_exp_a = np.sum(exp_a) y = exp_a / sum_exp_a return y x = np.arange(-10.0, 10.0, 1) y = softmax(x) plt.plot(x, y,color='red',label="softmax") plt.legend(loc='best') plt.title("softmax Function") plt.ylim(-0.1, 1.1) # 指定y轴的范围 plt.show()
3.5.2 实现 softmax函数时的注意事项
在计算机的运算 上有一定的缺陷。这个缺陷就是溢出问题。softmax 函数的实现中要进行指 数函数的运算,但是此时指数函数的值很容易变得非常大。比如,的值 会超过20000 ,
会变成一个后面有 40 多个 0 的超大值,
的结果会返回 一个表示无穷大的inf。如果在这些超大值之间进行除法运算,结果会出现“不确定”的情况。

a = np.array([1010, 1000, 990]) print("----------") print("softmax函数的运算={0}".format(np.exp(a) / np.sum(np.exp(a)) )) c = np.max(a) # 1010 print("----------") print("改进的softmax函数的运算={0}".format(np.exp(a - c) / np.sum(np.exp(a - c)))) 3.5.3 softmax函数的特征
3.5.3 softmax函数的特征#3.5.3 softmax函数的特征 a = np.array([0.3, 2.9, 4.0]) y = softmax(a) print("----------") print("softmax函数的运算={0}".format(y)) print("----------") print("输出总和={0}".format(np.sum(y)))
softmax 函数的输出是 0.0到1.0 之间的实数。并且, softmax 函数的输出值的总和是1 。输出总和为 1 是 softmax 函数的一个重要性质。正因为有了这个性质,我们才可以把softmax 函数的输出解释为“概率”。 比如,上面的例子可以解释成y[0] 的概率是 0 . 018 (1. 8 % ), y[1] 的概率 是0 . 245 ( 24 . 5 % ), y[2] 的概率是 0 . 737 ( 73 . 7 % )。从概率的结果来看,可以 说“因为第 2 个元素的概率最高,所以答案是第 2个类别”。而且,还可以回答“有74 % 的概率是第 2 个类别,有 25 % 的概率是第 1 个类别,有 1 % 的概 率是第0 个类别”。也就是说,通过使用 softmax 函数,我们可以用概率的(统计的)方法处理问题。这里需要注意的是,即便使用了 softmax 函数,各个元素之间的大小关 系也不会改变。这是因为指数函数 是单调递增函数。实际上,上例中a 的各元素的大小关系和 y 的各元素的大小关系并没有改变。比如, a 的最大值是第2 个元素, y 的最大值也仍是第 2 个元素。 一般而言,神经网络只把输出值最大的神经元所对应的类别作为识别结果。 并且,即便使用softmax 函数,输出值最大的神经元的位置也不会变。因此, 神经网络在进行分类时,输出层的softmax 函数可以省略。在实际的问题中, 由于指数函数的运算需要一定的计算机运算量,因此输出层的softmax 函数 一般会被省略。3.5.4 输出层的神经元数量输出层的神经元数量需要根据待解决的问题来决定。对于分类问题,输出层的神经元数量一般设定为类别的数量。3.6 手写数字识别
介绍完神经网络的结构之后,现在我们来试着解决实际问题。这里我们 来进行手写数字图像的分类。假设学习已经全部结束,我们使用学习到的参 数,先实现神经网络的“推理处理”。这个推理处理也称为神经网络的前向传播( forward propagation)。3.6.1 MNIST数据集数据集的介绍
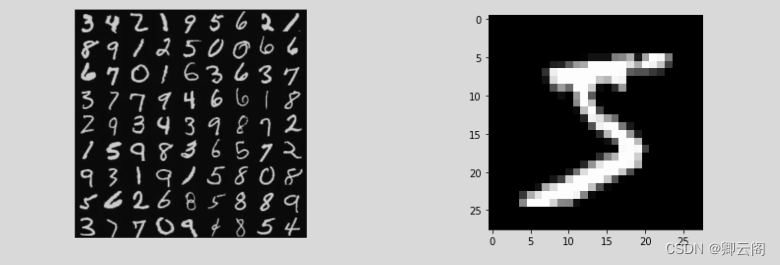
MNIST包含70000张手写数字图像:60000张用于训练;10000张用于测试。 28x28像素的灰度图。 MNIST的图像数据是28像素 × 28像素的灰度图像(通道),各个像素的取值在0到255之间。每个图像数据都相应地标有“7”“2”“1”等标签。 本书提供了便利的Python脚本mnist.py,该脚本支持从下载MNIST数据 集到将这些数据转换成NumPy数组等处理(mnist.py在dataset目录下)。使用 mnist.py时,当前目录必须是ch01、ch02、ch03、…、ch08目录中的一个。使 用mnist.py中的load_mnist()函数,就可以按下述方式轻松读入MNIST数据。
数字化 digitize
矩阵变换 reshape
归一化 normalization
独热编码 one-hot
问了防止因为有些数字很像,而造成训练不好的问题。
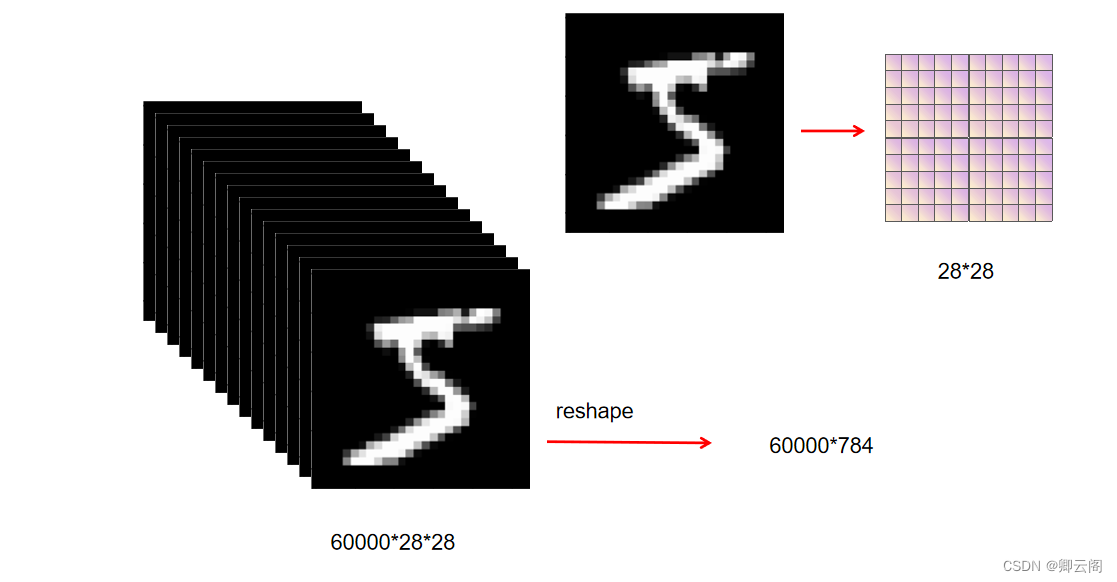
import sys, os sys.path.append(os.pardir) # 为了导入父目录中的文件而进行的设定 from dataset.mnist import load_mnist # 第一次调用会花费几分钟 …… (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True,normalize=False) # 输出各个数据的形状 print("-----训练集图片的形状-----") print(x_train.shape) # (60000, 784) print("-----训练集标签的形状-----") print(t_train.shape) # (60000,) print("-----测试集图片的形状-----") print(x_test.shape) # (10000, 784) print("-----测试集标签的形状-----") print(t_test.shape) # (10000,)load_mnist 函数以“ (训练图像 ,训练标签 ),(测试图像,测试标签 ) ”的形式返回读入的MNIST 数据。此外,还可以像 load_mnist(normalize=True, flatten=True,one_hot_label=False) 这 样,设 置 3 个 参 数。第 1 个参数normalize设置是否将输入图像正规化为 0 . 0 ~ 1 . 0 的值。如果将该参数设置 为False ,则输入图像的像素会保持原来的 0 ~ 255 。第 2 个参数 flatten 设置是否展开输入图像(变成一维数组)。如果将该参数设置为False ,则输入图 像为1 × 28 × 28 的三维数组;若设置为 True ,则输入图像会保存为由 784 个 元素构成的一维数组。第3 个参数 one_hot_label 设置是否将标签保存为 one-hot表示( one-hot representation )。 one-hot 表示是仅正确解标签为 1 ,其余 皆为0 的数组,就像 [0,0,1,0,0,0,0,0,0,0] 这样。 one_hot_label 为 False 时, 只是像7 、 2 这样简单保存正确解标签;当 one_hot_label 为 True 时,标签则保存为one-hot 表示。# coding: utf-8 import sys, os sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定 import numpy as np from dataset.mnist import load_mnist from PIL import Image def img_show(img): pil_img = Image.fromarray(np.uint8(img)) pil_img.show() (x_train, t_train), (x_test, t_test) = load_mnist(flatten=True, normalize=False) img = x_train[0] label = t_train[0] print("-----标签-----") print(label) print("-----其它特征-----") print(img.shape) # (784,) img = img.reshape(28, 28) # 把图像的形状变为原来的尺寸 print(img.shape) # (28, 28) img_show(img)
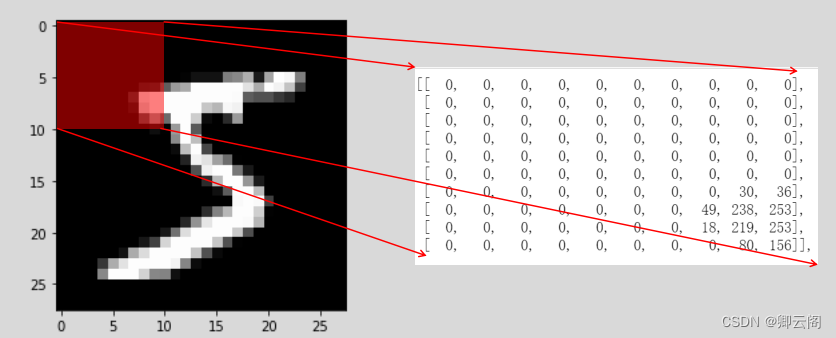
这里需要注意的是, flatten=True 时读入的图像是以一列(一维) NumPy 数组的形式保存的。因此,显示图像时,需要把它变为原来的28 像素 × 28 像素的形状。可以通reshape() 方法的参数指定期望的形状,更改 NumPy 数组的形状。此外,还需要把保存为NumPy 数组的图像数据转换为 PIL 用 的数据对象,这个转换处理由Image.fromarray() 来完成。3.6.2 神经网络的推理处理神经网络的输入层有784 个神经元,输出层有 10 个神经元。输入层的 784 这个数字来源于图像大小的 28 × 28 = 784 ,输出层的 10 这个数字来源于 10 类别分类(数字0 到 9 ,共 10 类别)。此外,这个神经网络有 2 个隐藏层,第 1 个隐藏层有 50个神经元,第 2 个隐藏层有 100 个神经元。这个 50 和 100 可以设置为任何值。 下面我们先定义get_data() 、 init_network() 、 predict() 这 3 个函数。# coding: utf-8 import sys, os sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定 import numpy as np import pickle from dataset.mnist import load_mnist def get_data(): (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False) return x_test, t_test def init_network(): with open("sample_weight.pkl", 'rb') as f: network = pickle.load(f) return network def predict(network, x): W1, W2, W3 = network['W1'], network['W2'], network['W3'] b1, b2, b3 = network['b1'], network['b2'], network['b3'] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = softmax(a3) return y x, t = get_data() network = init_network() accuracy_cnt = 0 for i in range(len(x)): y = predict(network, x[i]) p= np.argmax(y) # 获取概率最高的元素的索引 if p == t[i]: accuracy_cnt += 1 print("Accuracy:" + str(float(accuracy_cnt) / len(x)))init_network()会读入保存在pickle文件sample_weight.pkl中的学习到的权重参数。这个文件中以字典变量的形式保存了权重和偏置参数。剩余的2 个函数,和前面介绍的代码实现基本相同,无需再解释。现在,我们用这3 个函数来实现神经网络的推理处理。然后,评价它的识别精度(accuracy), 即能在多大程度上正确分类。
首先获得 MNIST 数据集,生成网络。接着,用 for 语句逐一取出保存在x 中的图像数据,用 predict() 函数进行分类。 predict() 函数以 NumPy 数组的形式输出各个标签对应的概率。比如输出[0.1, 0.3, 0.2, ..., 0.04] 的数组,该数组表示“0”的概率为 0.1,“1”的概率为0.3 ,等等。然后,我们取出这个概率列表中的最大值的索引(第几个元素的概率最高),作为预测结 果。可以用 np.argmax(x) 函数取出数组中的最大值的索引, np.argmax(x) 将 获取被赋给参数x 的数组中的最大值元素的索引。最后,比较神经网络所预测的答案和正确解标签,将回答正确的概率作为识别精度。执行上面的代码后,会显示“Accuracy:0 . 9352 ”。这表示有 93 . 52 % 的数据被正确分类了。目前我们的目标是运行学习到的神经网络,所以不讨论识别精度本身,不过以后我们会花精力在神经网络的结构和学习方法上,思考 如何进一步提高这个精度。实际上,我们打算把精度提高到99 % 以上。 另外,在这个例子中,我们把load_mnist 函数的参数 normalize 设置成了True。将 normalize 设置成 True 后,函数内部会进行转换,将图像的各个像 素值除以255 ,使得数据的值在 0 . 0 ~ 1 . 0 的范围内。像这样把数据限定到某个范围内的处理称为 正规化(normalization )。此外,对神经网络的输入数据进行某种既定的转换称为预处理 (pre-processing )。这里,作为对输入图像的一种预处理,我们进行了正规化。3.6.3 批处理以上就是处理 MNIST 数据集的神经网络的实现,现在我们来关注输入数据和权重参数的“形状”。再看一下刚才的代码实现。 下面我们使用Python 解释器,输出刚才的神经网络的各层的权重的形状。x, _ = get_data() network = init_network() W1, W2, W3 = network['W1'], network['W2'], network['W3'] print("-----测试集x的形状-----") print(x.shape) print("-----测试集第一张图片的形状-----") print(x[0].shape) print("-----第一层隐藏层权重的形状-----") print(W1.shape) print("-----第二层隐藏层权重的形状-----") print(W2.shape) print("-----第三层隐藏层权重的形状-----") print(W3.shape)
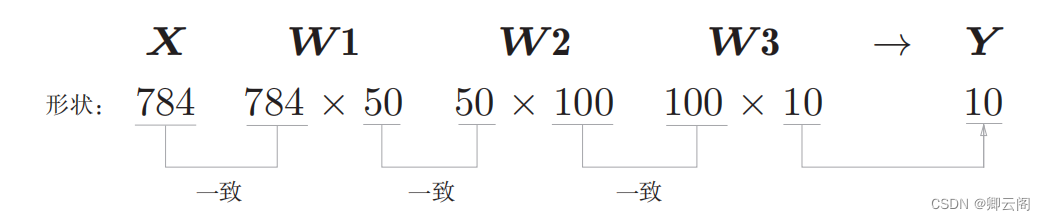 我们通过上述结果来确认一下多维数组的对应维度的元素个数是否一致 (省略了偏置)。用图表示的话,如图 所示。可以发现,多维数组的对应 维度的元素个数确实是一致的。此外,我们还可以确认最终的结果是输出了 元素个数为 10 的一维数组。从整体的处理流程来看 ,输入一个由 784 个元素(原本是一 个28 × 28 的二维数组)构成的一维数组后,输出一个有 10 个元素的一维数组。 这是只输入一张图像数据时的处理流程。现在我们来考虑打包输入多张图像的情形。比如,我们想用 predict() 函数一次性打包处理100 张图像。为此,可以把 x 的形状改为 100 × 784 ,将 100张图像打包作为输入数据 。
我们通过上述结果来确认一下多维数组的对应维度的元素个数是否一致 (省略了偏置)。用图表示的话,如图 所示。可以发现,多维数组的对应 维度的元素个数确实是一致的。此外,我们还可以确认最终的结果是输出了 元素个数为 10 的一维数组。从整体的处理流程来看 ,输入一个由 784 个元素(原本是一 个28 × 28 的二维数组)构成的一维数组后,输出一个有 10 个元素的一维数组。 这是只输入一张图像数据时的处理流程。现在我们来考虑打包输入多张图像的情形。比如,我们想用 predict() 函数一次性打包处理100 张图像。为此,可以把 x 的形状改为 100 × 784 ,将 100张图像打包作为输入数据 。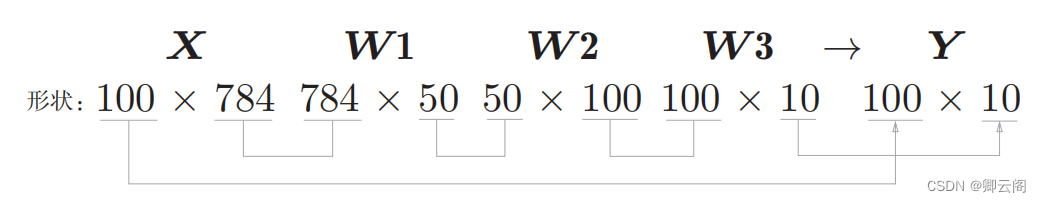 输入数据的形状为 100 × 784 ,输出数据的形状为 100 × 10 。这表示输入的 100 张图像的结果被一次性输出了。比如, x[0]和 y[0] 中保存了第 0 张图像及其推理结果, x[1] 和 y[1] 中保存了第 1 张图像及 其推理结果,等等。 这种打包式的输入数据称为批(batch)。
输入数据的形状为 100 × 784 ,输出数据的形状为 100 × 10 。这表示输入的 100 张图像的结果被一次性输出了。比如, x[0]和 y[0] 中保存了第 0 张图像及其推理结果, x[1] 和 y[1] 中保存了第 1 张图像及 其推理结果,等等。 这种打包式的输入数据称为批(batch)。# coding: utf-8 import sys, os sys.path.append(os.pardir) # 为了导入父目录的文件而进行的设定 import numpy as np import pickle from dataset.mnist import load_mnist def get_data(): (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, flatten=True, one_hot_label=False) return x_test, t_test def init_network(): with open("sample_weight.pkl", 'rb') as f: network = pickle.load(f) return network def predict(network, x): W1, W2, W3 = network['W1'], network['W2'], network['W3'] b1, b2, b3 = network['b1'], network['b2'], network['b3'] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = softmax(a3) return y x, t = get_data() network = init_network() batch_size = 100 # 批数量 accuracy_cnt = 0 for i in range(0, len(x), batch_size): x_batch = x[i:i+batch_size] y_batch = predict(network, x_batch) p = np.argmax(y_batch, axis=1) accuracy_cnt += np.sum(p == t[i:i+batch_size]) print("Accuracy:" + str(float(accuracy_cnt) / len(x)))我们来逐个解释粗体的代码部分。首先是 range() 函数。 range() 函数若指定range(start, end) ,则会生成一个由 start到end-1 之间的整数构成的列表。若像range(start, end, step) 这样指定 3 个整数,则生成的列表中的下一个元素会增加step 指定的值。我们来看一个例子。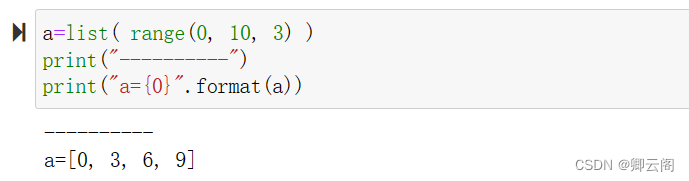
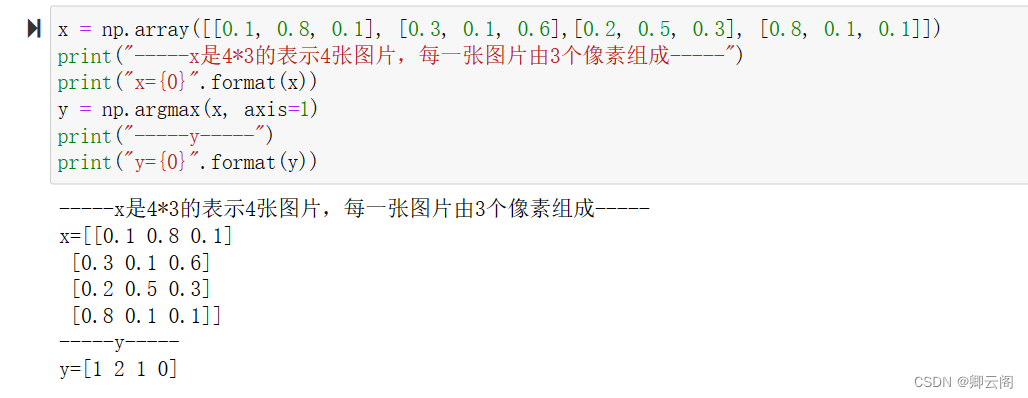
在 range() 函数生成的列表的基础上,通过 x[i:i+batch_size] 从输入数 据中抽出批数据。x[i:i+batch_n] 会取出从第 i 个到第 i+batch_n 个之间的数据。 本例中是像x[0:100] 、 x[100:200] ……这样,从头开始以 100 为单位将数据提 取为批数据。 然后,通过 argmax() 获取值最大的元素的索引。不过这里需要注意的是, 我们给定了参数 axis=1 。这指定了在 100 × 10 的数组中,沿着第 1 维方向(以第1 维为轴)找到值最大的元素的索引(第 0维对应第1 个维度)A。这里也来 看一个例子。、
最后,我们比较一下以批为单位进行分类的结果和实际的答案。为此, 需要在NumPy 数组之间使用比较运算符( == )生成由 True/False 构成的布尔型数组,并计算True 的个数。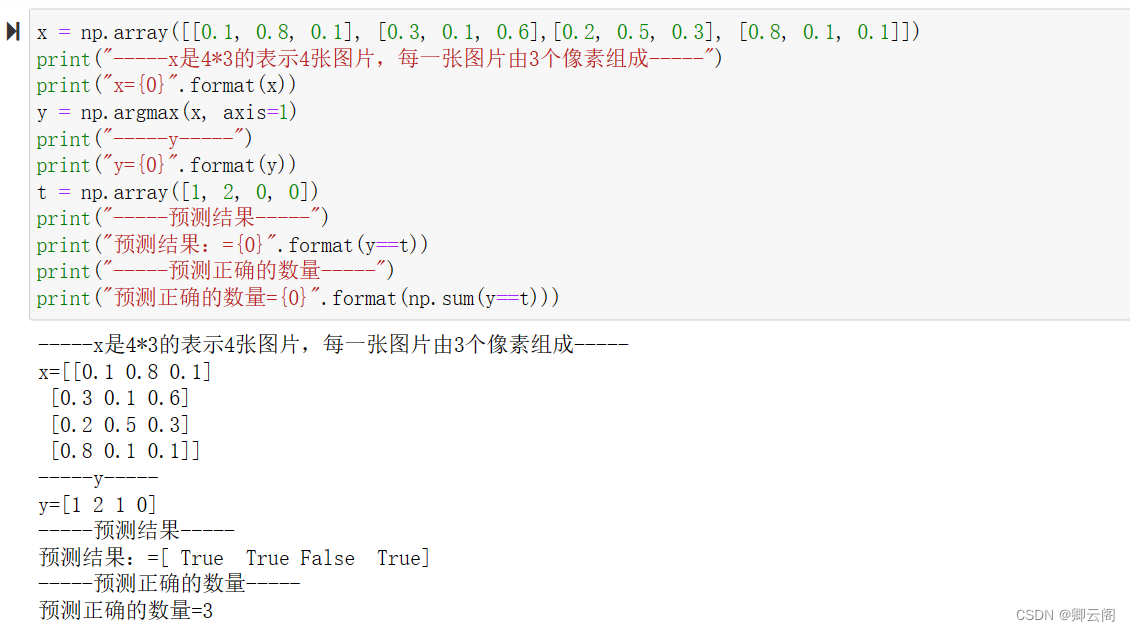
0基础入门---第3章---神经网络(前向传播)
news2026/2/7 18:41:26
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/648596.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
退出印度之后,越南制造也有麻烦,苹果摆脱中国制造成幻想
日前媒体报道指苹果在越南的代工厂面临麻烦,由于越南缺乏足够的电力供应,越南的工厂出现断电的问题,工厂生产被迫暂停,最严重的时候连续20天白天无法开工,这对于苹果来说无疑是又一个重大打击。 一、苹果的印度制造计划…
MODNet Background Remover 环境搭建步骤
1、安装 Python 3.8以上 2、安装 CUDA环境 4、下载 MODNet Background Remover 5、解压并进入到 MODNet Background Remover文件夹 6、创建虚拟环境
python -m venv venv7、使用虚拟环境
.\venv\Scripts\activate8、安装依赖包
pip install --upgrade pippip install --upg…
阿里云服务器租用费用_轻量和ECS价格表
2023年阿里云服务器租用费用,阿里云轻量应用服务器2核2G3M带宽轻量服务器一年108元,2核4G4M带宽轻量服务器一年297.98元12个月,阿里云u1服务器2核4G、2核8G、4核8G、8核16G、4核16G、8核64等配置新人3折,云服务器c7、g7和r7均有活…
VMware Horizon 8 运维系列(二)桌面计算机无法访问代理
前言 Horizon 8 在使用即时克隆桌面池,偶尔会出现某个桌面计算机显示“无法访问代理”状态,这时该计算机无法通过客户机来访问。 一、问题描述
1、问题场景
桌面池类型:即时克隆桌面池
2、查看桌面池
查看桌面池,发现有计算机状态为“无法访问代理“,如下图: 二、问题…
回归预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost多输入单输出回归预测
回归预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost多输入单输出回归预测 目录 回归预测 | MATLAB实现基于BiLSTM-AdaBoost双向长短期记忆网络结合AdaBoost多输入单输出回归预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现…
全民AI计划:通过langchain给LLM接上落地的大腿
langchain是一个开源项目 github.com/hwchase17/l… 。这个项目在GitHub上已经有45.5K个Star了。此项目由一位叫hwchase17的国外小哥在2022年底发布。
我有理由相信,这个项目是为了对接大语言模型才搞的。
一、企业困境: 如何应用大语言模型
大语言模型(Large La…
渗透专题丨web Top10 漏洞简述(2)
文件包含漏洞
1、漏洞简述
程序在引用文件的时,引用的文件名,用户可控的情况,传入的文件名校验不严,从而操作了预想之外的文件,就有可能导致文件泄漏和恶意的代码注入。这是因为程序开发时候会把重复使用的函数写到归…
springboot启动流程 (1) 流程概览
本文将通过阅读源码方式分析SpringBoot应用的启动流程,不涉及Spring启动部分(有相应的文章介绍)。
本文不会对各个流程做展开分析,后续会有文章介绍详细流程。
SpringApplication类
应用启动入口
使用以下方式启动一个SpringBoot应用:
S…
【计算机视觉】最近跑实验的感悟:大模型训练太难了!
文章目录 一、大模型训练太难了二、大模型的训练有三大难点三、OpenAI 的一些启发 一、大模型训练太难了
这里大模型训练特指基座大模型的从0开始训练,不包括在2000条数据上SFT这样的小任务。
有人说大模型嘛,简单,给我卡就行,等…
「2023」高频前端面试题汇总之JavaScript篇(上)
近期整理了一下高频的前端面试题,分享给大家一起来学习。如有问题,欢迎指正!
一、数据类型
1. JavaScript有哪些数据类型,它们的区别?
JavaScript共有八种数据类型,分别是 Undefined、Null、Boolean、N…
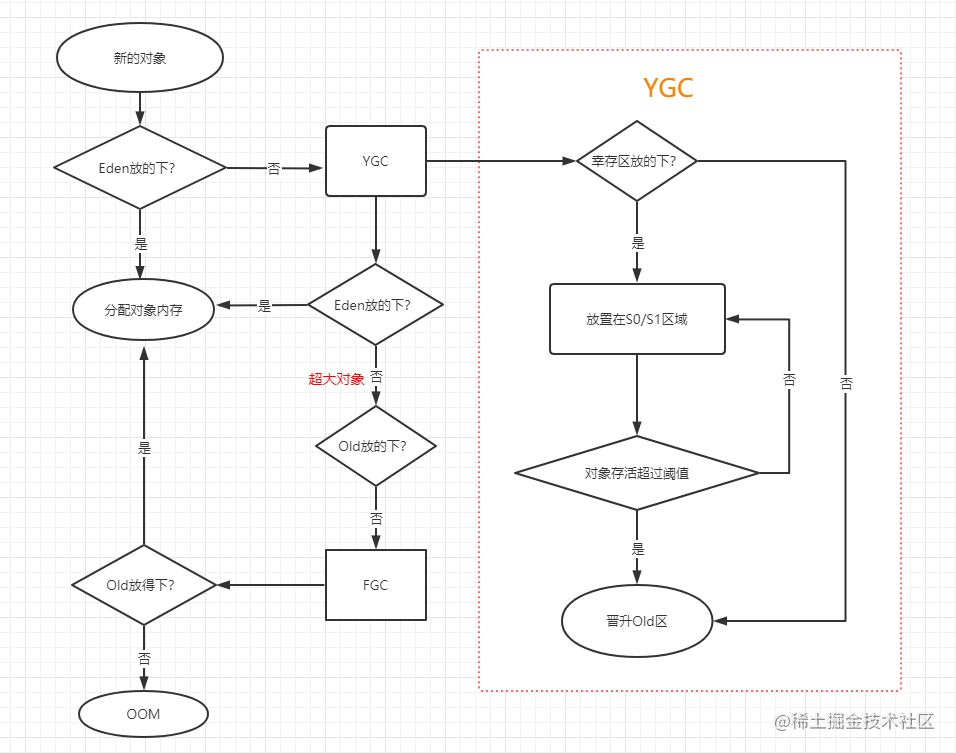
【JVM系列】内存分配与回收策略详解
文章目录 Minor GC 和 Full GC内存分配策略一般过程第一次轻GC第二次轻GC第N次GC 特殊过程小结 Full GC 的触发条件1. 调用 System.gc()2. 老年代空间不足3. 空间分配担保失败4. JDK 1.7 及以前的永久代空间不足5. Concurrent Mode Failure Minor GC 和 Full GC Minor GC&#…
基于DDD实现的用户注册流程,很优雅!
欢迎回来,我是飘渺。今天继续更新DDD&微服务的系列文章。 在前面的文章中,我们深入探讨了DDD的核心概念。我理解,对于初次接触这些概念的你来说,可能难以一次性完全记住。但别担心,学习DDD并不仅仅是理论的理解&am…
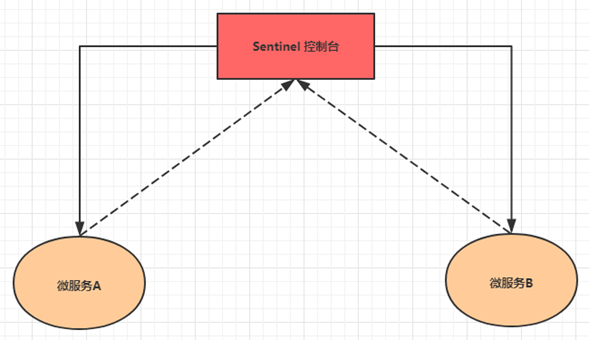
6.SpringCloudAlibaba 整合 Sentinel
一、分布式系统遇到的问题
1 服务雪崩效应
在分布式系统中,由于网络原因或自身的原因,服务一般无法保证 100%是可用的。如果一个服务出现了问题,调用这个服务就会出现线程阻塞的情况,此时若有大量的请求涌入,就会出现…
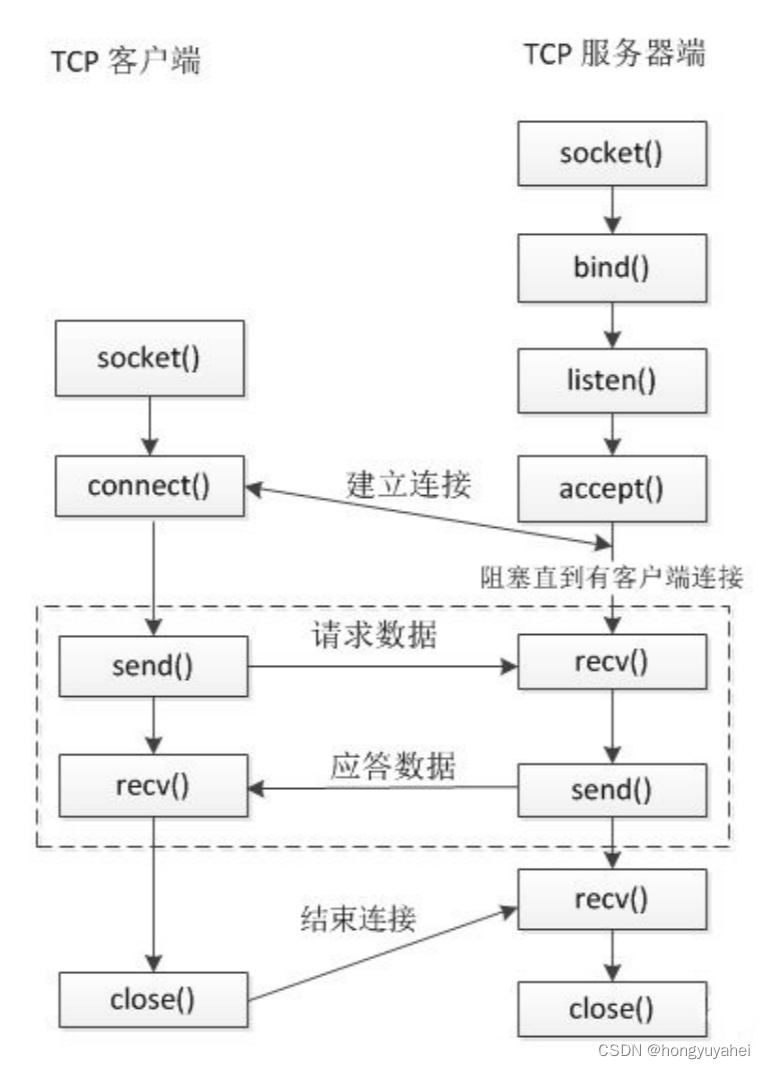
4.11 socket地址 4.12 IP地址转换函数 4.13TCP通信流程 4.14socket函数
4.11 socket地址
socket地址其实是一个结构体,封装端口号和IP等信息。后面的socket相关的api中需要使用到这个socket地址。 客户端 -> 服务器(IP, Port)
通用 socket地址
socket 网络编程接口中表示 socket 地址的是结构体 sockaddr&am…
安装Vue(重点笔记)
目录
什么是Vue?
特点
Node.js安装
Vue安装
1、安装Vue.js
1.1)安装失败解决
1.2)安装成功
2、安装webpack模板
3、安装脚手架
4、安装vue-router
创建第一个Vue-cli应用程序
1、命令行(cmd) cd 到指定的目录
2. 创建第一个基于webpack模…
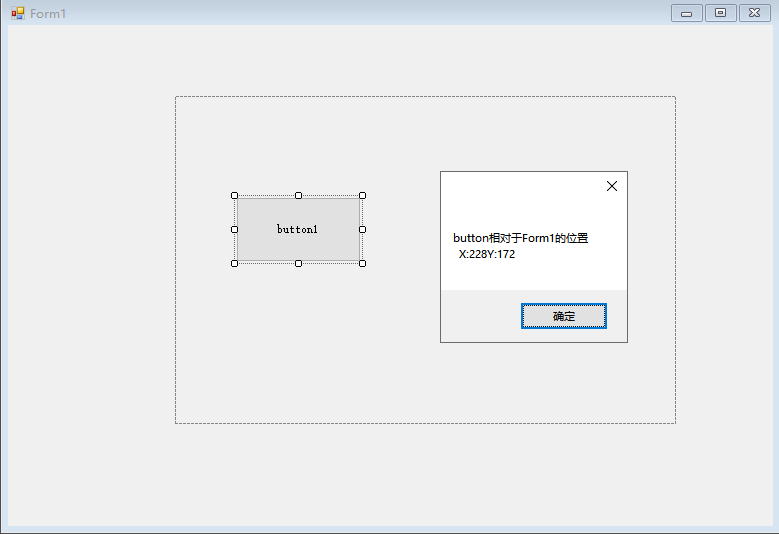
【C#】WinForm中如何获取一个控件相对于主界面的位置
文章目录 前言一、新建WinForm程序二、效果与代码总结 前言
使用button控件的 PointToScreen 方法和Form控件的 PointToClient 方法来获取button1相对于Form边界的位置。具体步骤如下:
获取button1在屏幕上的位置:
Point button1ScreenPos button1.P…
【TensorRT】TensorRT的环境配置
本文主要记录TensorRT8.6的环境配置过程!
官方文档:NVIDIA TensorRT - NVIDIA Docs
TensorRT相关版本的文档: Documentation Archives :: NVIDIA Deep Learning TensorRT Documentation 一 、下载CUDA和cudann
CUDA下载:CUDA T…
最近不知道写啥,打算整理点儿关于钱币的文章,也转载点儿别人的技术文章,毕竟,洒家还是干技术滴嘛...
最近开始整理之前陆陆续续买的乱七八糟的东西了,现在一堆东西还乱扔着呢~~ 先整理了一套大五帝钱还有下面这套清五帝。 清五帝钱一套: 27宝泉局顺治通宝,铁壳锈 27.5康熙通宝满汉同 26.5宝泉局雍正通宝 三离划 26(卡)宝云局乾隆通…
Vision Transformer综述 总篇
Vision Transformer综述 1. Transformer简介2. Transformer组成2.1 Self-AttentionMulti-Head Attention(多头注意力) 2.2 Transformer的其他关键概念2.2.1 Feed-Forward Network 前馈网络2.2.2 Residual Connection 残差连接2.2.3 解码器中的最后一层 3…
Go GC:了解便利背后的开销
1. 简介 当今,移动互联网和人工智能的快(越)速(来)发(越)展(卷),对编程语言的高效性和便利性提出了更高的要求。Go作为一门高效、简洁、易于学习的编程语言,受到了越来越多开发者的青睐。 Go语言的垃圾回收机制(Garbage Collectio…