单位圆是半径为 1.0 的圆。
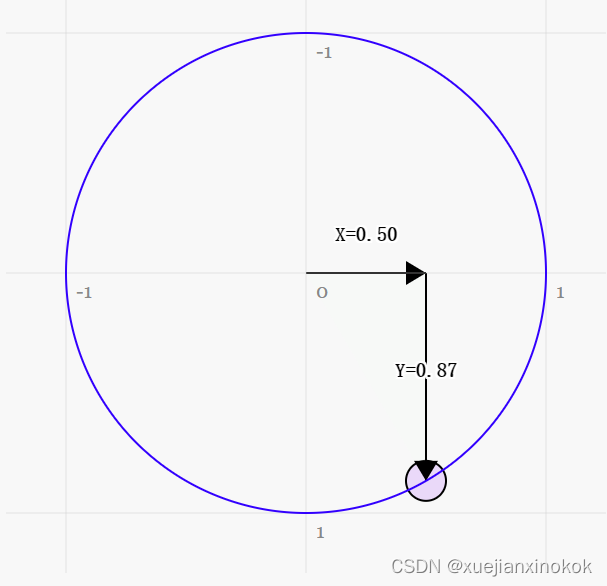
下图是一个单位圆。 [注释1]
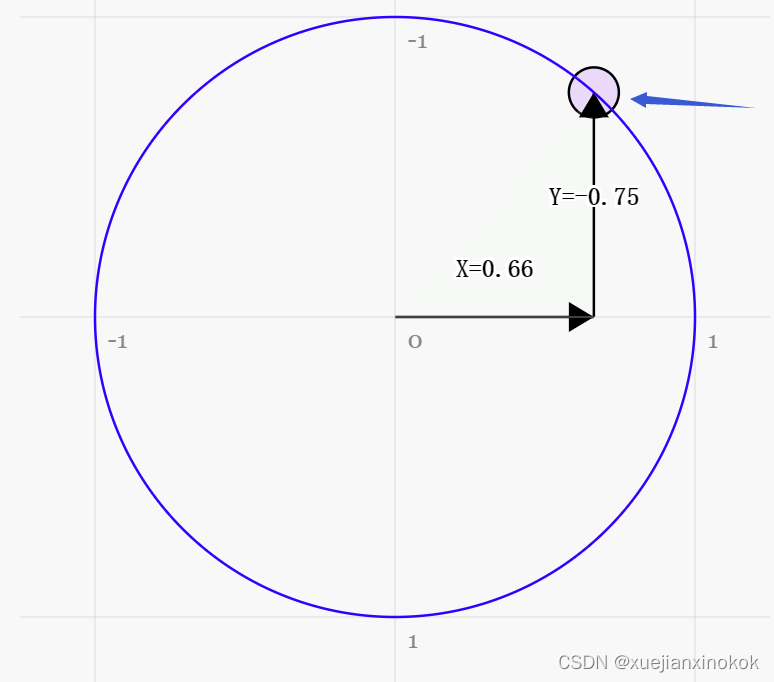
在上图中,当围绕圆拖动蓝色手柄时,X 和 Y 位置会发生变化,代表该点在圆上的位置。且在顶部,Y 为 1,X 为 0。在右侧,X 为 1,Y 为 0。
如果你还记得三年级的基础数学,将某个东西乘以 1,它会保持不变。所以 123 * 1 = 123。很基础,对吧?好吧,一个单位圆,一个半径为 1.0 的圆也是 1 的一种形式。它是一个旋转的 1。所以可以用这个单位圆乘以一些东西,在某种程度上它有点像乘以 1。
我们将从单位圆上的任意点获取 X 和 Y 值,并将顶点位置乘以之前示例中的值。
下边是着色器的修改。
struct Uniforms {
color: vec4f,
resolution: vec2f,
translation: vec2f,
rotation: vec2f,
};
struct Vertex {
@location(0) position: vec2f,
};
struct VSOutput {
@builtin(position) position: vec4f,
};
@group(0) @binding(0) var<uniform> uni: Uniforms;
@vertex fn vs(vert: Vertex) -> VSOutput {
var vsOut: VSOutput;
// Rotate the position
let rotatedPosition = vec2f(
vert.position.x * uni.rotation.x - vert.position.y * uni.rotation.y, //here
vert.position.x * uni.rotation.y + vert.position.y * uni.rotation.x //here
);
// Add in the translation
// let position = vert.position + uni.translation;
let position = rotatedPosition + uni.translation;
// convert the position from pixels to a 0.0 to 1.0 value
let zeroToOne = position / uni.resolution;
// convert from 0 <-> 1 to 0 <-> 2
let zeroToTwo = zeroToOne * 2.0;
// covert from 0 <-> 2 to -1 <-> +1 (clip space)
let flippedClipSpace = zeroToTwo - 1.0;
// flip Y
let clipSpace = flippedClipSpace * vec2f(1, -1);
vsOut.position = vec4f(clipSpace, 0.0, 1.0);
return vsOut;
}
更新了 JavaScript 增加 uniform 的大小。
// color, resolution, translation
//const uniformBufferSize = (4 + 2 + 2) * 4;
// color, resolution, translation, rotation, padding
const uniformBufferSize = (4 + 2 + 2 + 2) * 4 + 8; //here
const uniformBuffer = device.createBuffer({
label: 'uniforms',
size: uniformBufferSize,
usage: GPUBufferUsage.UNIFORM | GPUBufferUsage.COPY_DST,
});
const uniformValues = new Float32Array(uniformBufferSize / 4);
// offsets to the various uniform values in float32 indices
const kColorOffset = 0;
const kResolutionOffset = 4;
const kTranslationOffset = 6;
const kRotationOffset = 8; //here
const colorValue = uniformValues.subarray(kColorOffset, kColorOffset + 4);
const resolutionValue = uniformValues.subarray(kResolutionOffset, kResolutionOffset + 2);
const translationValue = uniformValues.subarray(kTranslationOffset, kTranslationOffset + 2);
const rotationValue = uniformValues.subarray(kRotationOffset, kRotationOffset + 2); //here
我们需要UI用于显示。这篇文章不是关于制作 UI 的教程,所以我只打算使用一个。首先是一些 HTML 给 单位圆 一个占位
<body>
<canvas></canvas>
<div id="circle"></div>
</body>
然后是一些用于定位的 CSS
#circle {
position: fixed;
right: 0;
bottom: 0;
width: 300px;
background-color: var(--bg-color);
}
最后是使用它的 JavaScript。
import UnitCircle from './resources/js/unit-circle.js'; //here
...
const gui = new GUI();
gui.onChange(render);
gui.add(settings.translation, '0', 0, 1000).name('translation.x');
gui.add(settings.translation, '1', 0, 1000).name('translation.y');
const unitCircle = new UnitCircle(); //here
document.querySelector('#circle').appendChild(unitCircle.domElement); //here
unitCircle.onChange(render); //here
function render() {
...
// Set the uniform values in our JavaScript side Float32Array
resolutionValue.set([canvas.width, canvas.height]);
translationValue.set(settings.translation);
rotationValue.set([unitCircle.x, unitCircle.y]); //here
// upload the uniform values to the uniform buffer
device.queue.writeBuffer(uniformBuffer, 0, uniformValues);
下边是显示结果。拖动圆圈上的手柄进行旋转或拖动滑块进行平移。
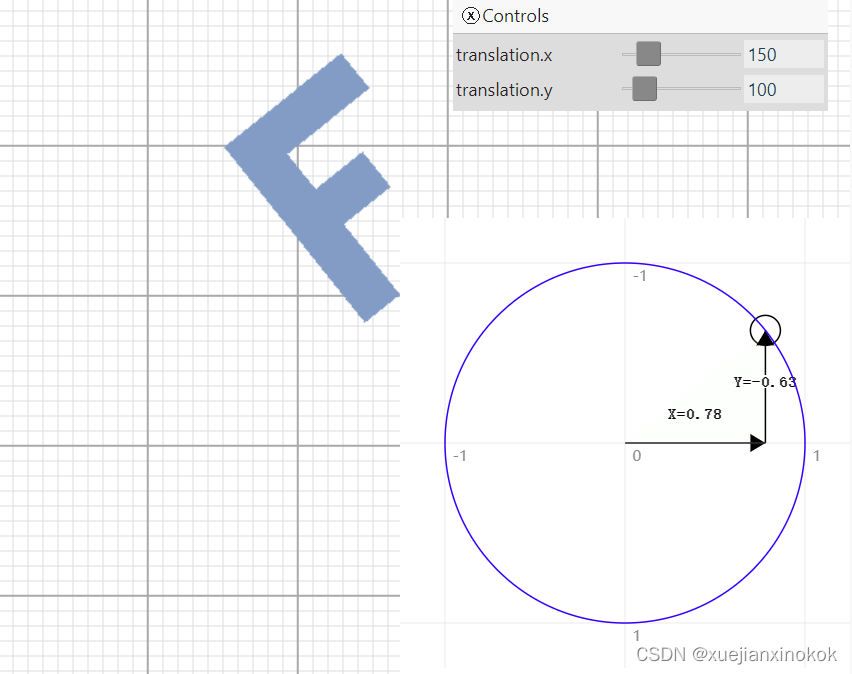
为什么它会起作用?这里用数学解释一下。
rotatedX = a_position.x * u_rotation.x - a_position.y * u_rotation.y;
rotatedY = a_position.x * u_rotation.y + a_position.y * u_rotation.x;
假设有一个矩形并且想要旋转它。在开始旋转之前,右上角位于( 3.0,-9.0)。让我们在单位圆上从 3 点钟方向顺时针 30 度取一个点。
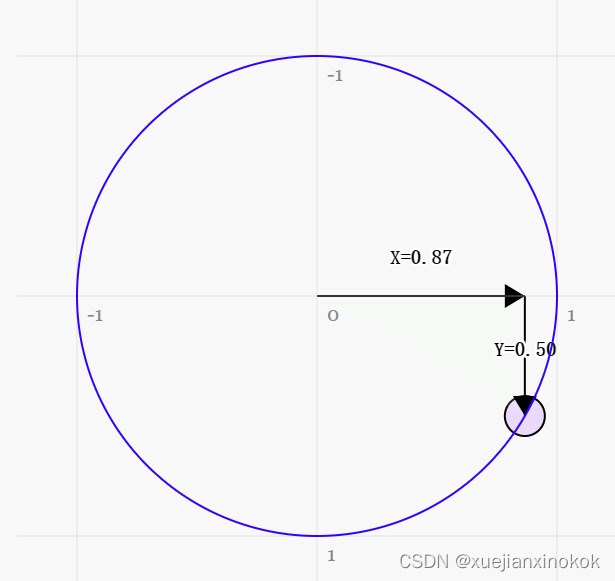
上图圆上的位置是x = 0.87, y = 0.50
3.0 * 0.87 - -9.0 * 0.50 = 7.1
3.0 * 0.50 + -9.0 * 0.87 = -6.3
这正是它旋转后的地方
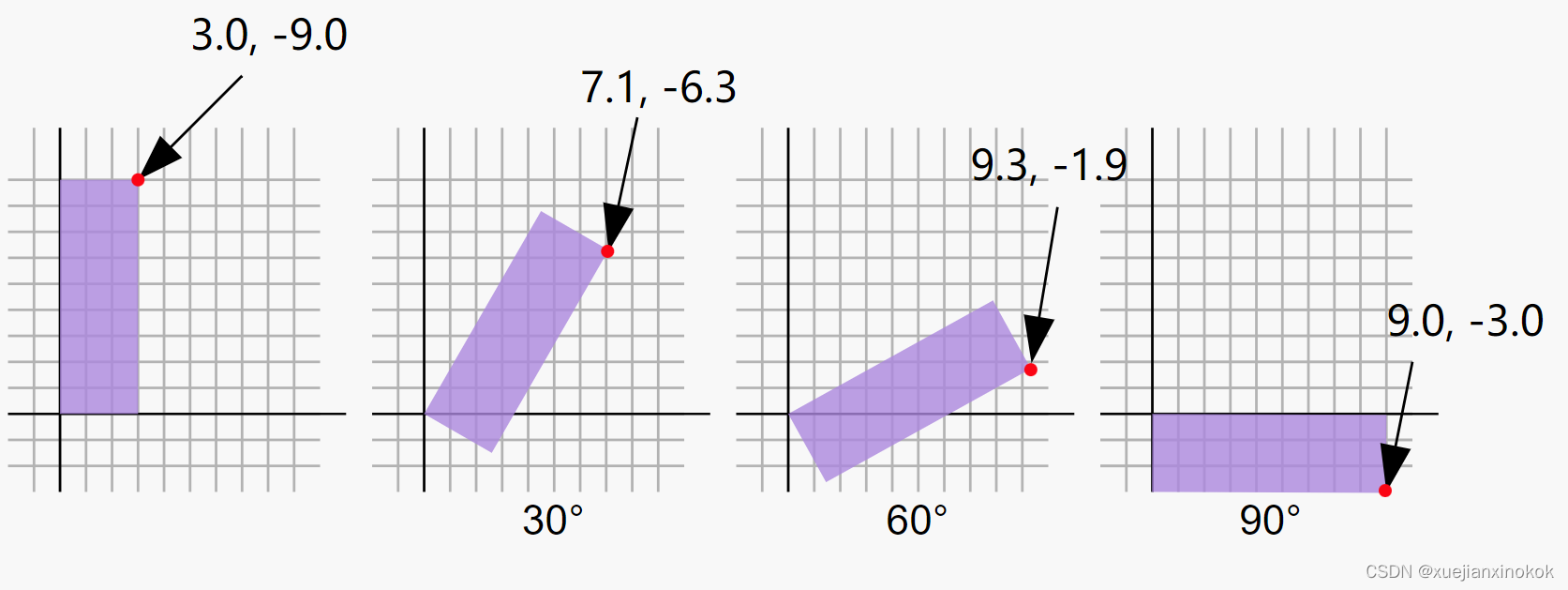
同样的取顺时针60度
圆圈上的位置是 0.87 和 0.50
3.0 * 0.50 - -9.0 * 0.87 = 9.3
3.0 * 0.87 + -9.0 * 0.50 = -1.9
可以看到,当顺时针旋转该点时,X 值变大,Y 值变小。如果继续超过 90 度,X 将再次开始变小,而 Y 将开始变大。这种模式会交替轮换。
单位圆上的点还有另一个名字。它们被称为正弦和余弦。所以对于任何给定的角度,可以像这样获取正弦和余弦。
function printSineAndCosineForAnAngle(angleInDegrees) {
const angleInRadians = angleInDegrees * Math.PI / 180;
const s = Math.sin(angleInRadians);
const c = Math.cos(angleInRadians);
console.log('s =', s, 'c =', c);
}
如果将代码复制并粘贴到 JavaScript 控制台并键入 printSineAndCosignForAngle(30) ,会看到它打印出 s = 0.50 c = 0.87 (注意:我对数字进行了四舍五入)
如果把它们放在一起,可以将顶点位置旋转到想要的任何角度。只需将旋转设置为要旋转到的角度的正弦和余弦。
...
const angleInRadians = angleInDegrees * Math.PI / 180;
rotation[0] = Math.cos(angleInRadians);
rotation[1] = Math.sin(angleInRadians);
下边把代码改成只有一个旋转参数。
const degToRad = d => d * Math.PI / 180;
const settings = {
translation: [150, 100],
rotation: degToRad(30),//here
};
const radToDegOptions = { min: -360, max: 360, step: 1, converters: GUI.converters.radToDeg };
const gui = new GUI();
gui.onChange(render);
gui.add(settings.translation, '0', 0, 1000).name('translation.x');
gui.add(settings.translation, '1', 0, 1000).name('translation.y');
gui.add(settings, 'rotation', radToDegOptions);
// const unitCircle = new UnitCircle();
// document.querySelector('#circle').appendChild(unitCircle.domElement);
// unitCircle.onChange(render);
function render() {
...
// Set the uniform values in our JavaScript side Float32Array
resolutionValue.set([canvas.width, canvas.height]);
translationValue.set(settings.translation); //here
// rotationValue.set([unitCircle.x, unitCircle.y]);
rotationValue.set([
Math.cos(settings.rotation), //here
Math.sin(settings.rotation), //here
]);
拖动滑块以平移或旋转。
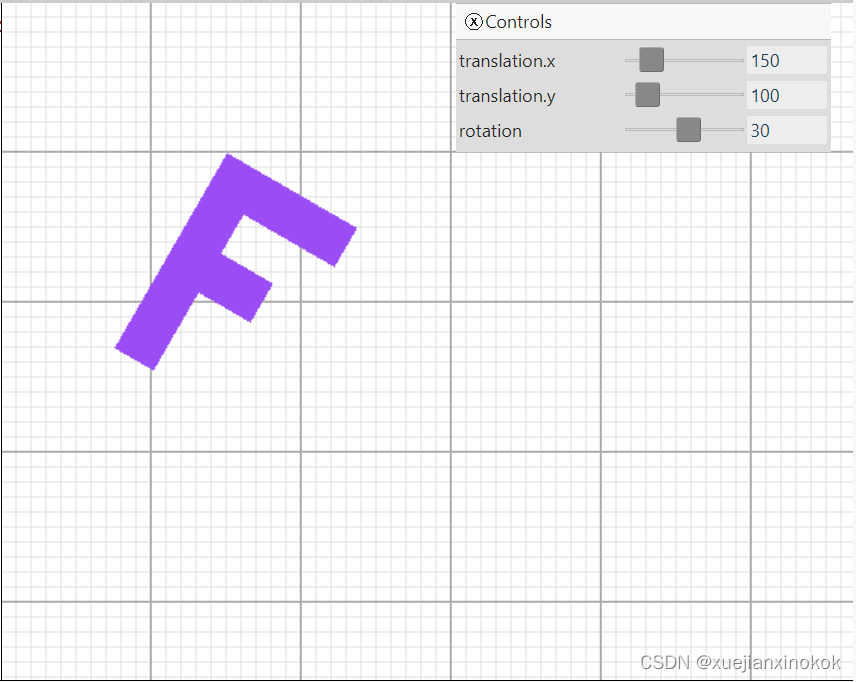
我希望这很符合直觉。接下来是一个更简单的。缩放变换。
注释1
什么是弧度(radians)?
弧度是用于圆、旋转和角度的测量单位。就像我们可以以英寸、码、米等为单位测量距离一样,我们可以以度数或弧度来测量角度。
您可能知道公制测量的数学比英制测量的数学更容易。从英寸到英尺,我们除以 12。从英寸到码,我们除以 36。我不了解你,但我无法在脑海中除以 36。使用公制就容易多了。从毫米换算成厘米,我们除以 10。从毫米换算成米,我们除以 1000。我可以在脑海中除以 1000。
弧度与度数相似。角度使数学变得困难。弧度使数学变得简单。一个圆有 360 度,但只有 2π 弧度。所以一整圈是 2π 弧度。半圈是 1π 弧度。 1/4 圈,即 90 度是 1/2π 弧度。所以如果你想将某物旋转 90 度,只需使用 Math.PI * 0.5 。如果你想将其旋转 45 度,请使用 Math.PI * 0.25 等。
如果您开始考虑弧度,几乎所有涉及角度、圆或旋转的数学运算都非常简单。所以试试吧。使用弧度而不是角度,UI 显示除外。
这个单位圆有 +Y 向下以匹配我们的像素空间也是 Y 向下。 WebGPU 的正常剪辑空间是 +Y 向上。在上一篇文章中,我们已经在着色器中翻转了 Y。
原文地址