快速傅里叶变换python实现

一、前言

　　我想认真写好快速傅里叶变换(Fast Fourier Transform，FFT)，所以这篇文章会由浅到细，由窄到宽的讲解，但是傅里叶变换对于寻常人并不是很容易理解的，所以对于基础不牢的人我会通过前言普及一下相关知识。

　　我们复习一下三角函数的标准式：$$y=A\cos (\omega x+\theta )+k$$

　　\(A\)代表振幅，函数周期是\(\frac{2\pi}{w}\)，频率是周期的倒数\(\frac{w}{2\pi}\)，\(\theta\)是函数初相位，\(k\)在信号处理中称为直流分量。这个信号在频域就是一条竖线。

　　我们再来假设有一个比较复杂的时域函数\(y=f(t)\)，根据傅里叶的理论，任何一个周期函数可以被分解为一系列振幅\(A\)，频率\(\omega\)
或初相位\(\theta\)正弦函数的叠加

\[y = A_1sin(\omega_1t+\theta_1) +  A_2sin(\omega_2t+\theta_2) +  A_3sin(\omega_3t+\theta_3) \]

　　该信号在频域有三条竖线组成，而竖线图我们把它称为频谱图，大家可以通过下面的动画了解

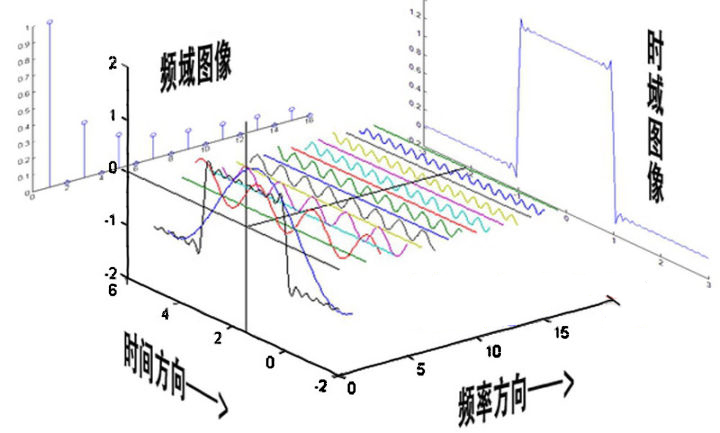
　如图可知，通过时域到频域的变换，我们得到了一个从侧面看的频谱，但是这个频谱并没有包含时域中全部的信息。因为频谱只代表每个正弦波对应频率的振幅是多少，而没有提到相位。基础的正弦波\(Asin(wt+\theta )\)中，振幅，频率，相位缺一不可，不同相位决定了波的位置，所以对于频域分析，仅仅有频谱(振幅谱)是不够的，我们还需要一个相位谱。

　　我依稀记得高中学正弦函数的是时候，\(\theta\)的多少决定了正弦波向右移动多少。当然那个时候横坐标是相位角度，而时域信号的横坐标是时间，因此我们只需要将时间转换为相位角度就得到了初相位。相位差则是时间差在一个周期中所占的比例

\[\theta=2\pi \frac{t}{T} \]

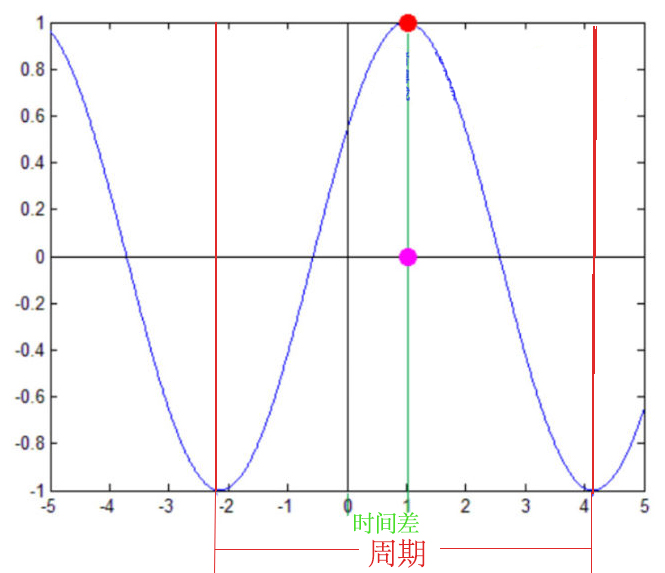
所以傅里叶变换可以把一个比较复杂的函数转换为多个简单函数的叠加，将时域(即时间域)上的信号转变为频域(即频率域)上的信号，看问题的角度也从时间域转到了频率域，因此在时域中某些不好处理的地方，在频域就可以较为简单的处理，这就可以大量减少处理信号计算量。\(\color{FF0000}{信号经过傅里叶变换后，可以得到频域的幅度谱以及相位谱，信号的幅度谱和相位谱是信号傅里叶变换后频谱的两个属性}\)

傅里叶用途

• 时域复杂的函数，在频域就是几条竖线
• 求解微分方程，傅里叶变换则可以让微分和积分在频域中变为乘法和除法

傅里叶变换相关函数

　　假设我们的输入信号的函数是

\[S=0.2+0.7*\cos (2\pi*50t+\frac{20}{180}\pi)+0.2*\cos (2\pi*100t+\frac{70}{180}\pi) \]

可以发现直流分量是0.2，以及两个余弦函数的叠加，余弦函数的幅值分别为0.7和0.2，频率分别为50和100，初相位分别为20度和70度。
freqs = np.fft.fftfreq(采样数量, 采样周期)通过采样数与采样周期得到时域序列经过傅里叶变换后的频率序列np.fft.fft(原序列)原函数值的序列经过快速傅里叶变换得到一个复数数组，复数的模代表的是振幅，复数的辐角代表初相位np.fft.ifft(复数序列)复数数组经过逆向傅里叶变换得到合成的函数值数组

案例：针对合成波做快速傅里叶变换，得到分解波数组的频率、振幅、初相位数组，并绘制频域图像。

import matplotlib.pyplot as plt 
import numpy as np
import numpy.fft as fft

plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示符号

Fs = 1000;            # 采样频率
T = 1/Fs;             # 采样周期
L = 1000;             # 信号长度
t = [i*T for i in range(L)]
t = np.array(t)

S = 0.2+0.7*np.cos(2*np.pi*50*t+20/180*np.pi) + 0.2*np.cos(2*np.pi*100*t+70/180*np.pi) ;


complex_array = fft.fft(S)
print(complex_array.shape)  # (1000,) 
print(complex_array.dtype)  # complex128 
print(complex_array[1])  # (-2.360174309695419e-14+2.3825789764340993e-13j)

#################################
plt.subplot(311)
plt.grid(linestyle=':')
plt.plot(1000*t[1:51], S[1:51], label='S')  # y是1000个相加后的正弦序列
plt.xlabel("t(毫秒)")
plt.ylabel("S(t)幅值")
plt.title("叠加信号图")
plt.legend()

###################################
plt.subplot(312)
S_ifft = fft.ifft(complex_array)
# S_new是ifft变换后的序列
plt.plot(1000*t[1:51], S_ifft[1:51], label='S_ifft', color='orangered')
plt.xlabel("t(毫秒)")
plt.ylabel("S_ifft(t)幅值")
plt.title("ifft变换图")
plt.grid(linestyle=':')
plt.legend()

###################################
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅(能量大小)
pows = np.abs(complex_array)

plt.subplot(313)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs > 0], pows[freqs > 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()

基于傅里叶变换的频域滤波

从某条曲线中除去一些特定的频率成份，这在工程上称为“滤波”。

含噪信号是高能信号与低能噪声叠加的信号，可以通过傅里叶变换的频域滤波实现降噪。

通过FFT使含噪信号转换为含噪频谱，去除低能噪声，留下高能频谱后再通过IFFT留下高能信号。

案例：基于傅里叶变换的频域滤波为音频文件去除噪声(noiseed.wav数据集地址)。

　　1、读取音频文件，获取音频文件基本信息：采样个数，采样周期，与每个采样的声音信号值。绘制音频时域的：时间/位移图像

import numpy as np
import numpy.fft as nf
import scipy.io.wavfile as wf
import matplotlib.pyplot as plt

# 读取音频文件
sample_rate, noised_sigs = wf.read('./da_data/noised.wav')
print(sample_rate)  # sample_rate：采样率44100
print(noised_sigs.shape)    # noised_sigs:存储音频中每个采样点的采样位移(220500,)
times = np.arange(noised_sigs.size) / sample_rate

plt.figure('Filter')
plt.subplot(221)
plt.title('Time Domain', fontsize=16)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], noised_sigs[:178], c='orangered', label='Noised')
plt.legend()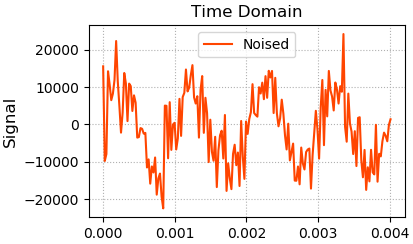

　　2、基于傅里叶变换，获取音频频域信息，绘制音频频域的：频率/能量图像

# 傅里叶变换后，绘制频域图像
freqs = nf.fftfreq(times.size, times[1] - times[0])
complex_array = nf.fft(noised_sigs)
pows = np.abs(complex_array)

plt.subplot(222)
plt.title('Frequency Domain', fontsize=16)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
# 指数增长坐标画图
plt.semilogy(freqs[freqs > 0], pows[freqs > 0], c='limegreen', label='Noised')
plt.legend()

　　3、将低频噪声去除后绘制音频频域的：频率/能量图像

# 寻找能量最大的频率值
fund_freq = freqs[pows.argmax()]
# where函数寻找那些需要抹掉的复数的索引
noised_indices = np.where(freqs != fund_freq)
# 复制一个复数数组的副本，避免污染原始数据
filter_complex_array = complex_array.copy()
filter_complex_array[noised_indices] = 0
filter_pows = np.abs(filter_complex_array)

plt.subplot(224)
plt.xlabel('Frequency', fontsize=12)
plt.ylabel('Power', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs >= 0], filter_pows[freqs >= 0], c='dodgerblue', label='Filter')
plt.legend()

　　4、基于逆向傅里叶变换，生成新的音频信号，绘制音频时域的：时间/位移图像

filter_sigs = nf.ifft(filter_complex_array).real
plt.subplot(223)
plt.xlabel('Time', fontsize=12)
plt.ylabel('Signal', fontsize=12)
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(times[:178], filter_sigs[:178], c='hotpink', label='Filter')
plt.legend()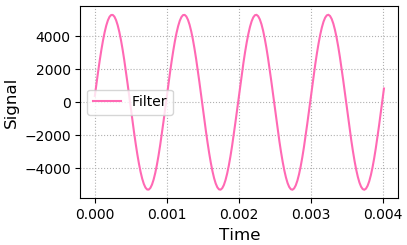

　　5、重新生成音频文件

# 生成音频文件
wf.write('./da_data/filter.wav', sample_rate, filter_sigs)
plt.show()

离散傅里叶变换 (DFT)

　　离散傅里叶变换(DFT)对有限长时域离散信号的频谱进行等间隔采样，频域函数被离散化了，便于信号的计算机处理。DFT的运算量太大，FFT是离散傅里叶变换的快速算法。

　　说白了FFT和DFT它俩就是一个东东，只不过复杂度不同，

　　有时候我们能够看到N点傅里叶变换，我个人理解是这个N点是信号前面N个连续的数值，即N点FFT意思就是截取前面N个信号进行FFT，这样就要求我们的前N个采样点必须包含当前信号的一个周期，不然提取的余弦波参数与正确的叠加波的参数相差很大。

　　如果在N点FFT的时候，如果这N个采样点不包含一个周期呢？或者说我们的信号压根不是一个周期函数咋办？或者有一段是噪音数据呢？如果用FFT计算，就会对整体结果影响很大，然后就有人想通过局部来逼近整体，跟微积分的思想很像，将信号分成一小段一小段，然后对每一小段做FFT，就跟分段函数似的，无数个分段函数能逼近任意的曲线((⊙o⊙)…应该没错吧)，这样每一段都不会互相影响到了。

二、短时傅里叶变换 (STFT)

　　在短时傅里叶变换过程中，窗的长度决定频谱图的时间分辨率和频率分辨率，窗长越长，截取的信号越长，信号越长，傅里叶变换后频率分辨率越高，时间分辨率越差；相反，窗长越短，截取的信号就越短，频率分辨率越差，时间分辨率越好，也就是说短时傅里叶变换中，时间分辨率和频率分辨率之间不能兼得，应该根据具体需求进行取舍。

计算短时傅里叶变换，需要指定的有：

• 每个窗口的长度：nsc
• 每相邻两个窗口的重叠率：nov
• 每个窗口的FFT采样点数：nff

可以计算的有：

• 海明窗：w=hamming(nsc, 'periodic')
• 信号被分成了多少片

python库librosa实现

librosa.stft(y, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')

短时傅立叶变换(STFT)，返回一个复数矩阵使得D(f,t)

参数：

• y：音频时间序列
• n_fft：FFT窗口大小，n_fft=hop_length+overlapping
• hop_length：帧移，如果未指定，则默认win_length / 4。
• win_length：每一帧音频都由window()加窗。窗长win_length，然后用零填充以匹配N_FFT。默认win_length=n_fft。
• window：字符串，元组，数字，函数 shape =(n_fft, )
  • 窗口(字符串，元组或数字)；
  • 窗函数，例如scipy.signal.hanning
  • 长度为n_fft的向量或数组
• center：bool
  • 如果为True，则填充信号y，以使帧 D [:, t]以y [t * hop_length]为中心。
  • 如果为False，则D [:, t]从y [t * hop_length]开始
• dtype：D的复数值类型。默认值为64-bit complex复数
• pad_mode：如果center = True，则在信号的边缘使用填充模式。默认情况下，STFT使用reflection padding。

返回：

• STFT矩阵D，shape =(1 +\(\frac{n_{fft} }{2}\)，t)

librosa.magphase(D, power=1)

将复值频谱D分离成其幅度(S)和相位(P)

参数：

• D：复值谱图，np.ndarray [shape =(d，t)，dtype = complex]
• power：幅度谱图的指数，例如，1代表能量，2代表功率，等等。

返回：

• D_mag ：D的幅值，np.ndarray [shape =(d，t)，dtype = real]
• D_phase ：D的相位，np.ndarray [shape =(d，t)，dtype = complex]，exp(1.j * phi)其中phi是D的相位

y, _ = librosa.load("p225_002.wav", sr=16000)

D = librosa.stft(y, n_fft=2048, hop_length=None, win_length=None, window='hann', center=True, pad_mode='reflect')
print(D.shape)    # (1025, 127)

# 将复值频谱D分离成其幅度(S)和相位(P)的部件
magnitude, phase = librosa.magphase(D, power=1)
# magnitude        # 赋值 [shape =(d，t)，dtype = real] (1025, 127)
# phase.shape    # 相位 [shape =(d，t)，dtype = complex] (1025, 127) 

angle = np.angle(phase)     # 获取相角(以弧度为单位)

tensorflow实现

一句话实现分帧、加窗、STFT变换

# [batch_size, signal_length].  batch_size and signal_length 可能会不知道
signals = tf.placeholder(tf.float32, [None, None])

# `stfts` 短时傅里叶变换：就是对信号中每一帧信号进行傅里叶变换 
# shape is [batch_size, ?, fft_unique_bins]
# 其中 fft_unique_bins = fft_length // 2 + 1 = 513.
stfts = tf.contrib.signal.stft(signals, frame_length=1024, frame_step=512,
                                                            fft_length=1024)

• wlen：窗长

• frame_length是信号中帧的长度

• frame_step是帧移

• fft_length：做fft变换的长度，或一种说话：fft变换所取得N点数，在有些地方也表示为NFFT。

注意：FFT的长度必须大于或者等于win的长度或者帧长。以获得更高的频域分辨率

FFT后的分辨率(频率的间隔)为fs/NFFT。当NFFT>wlen时就是在数据补零后做FFT，做的FFT得到的频谱等于以wlen长数据FFT的频谱中内插。

torch实现

spec_complex = torch.stft(x,nfft=256,hop_length=128,win_length=256,window=None,normalized=False,return_complex=False)
mag = torch.sqrt(spec_complex[:,0]**2 +spec_complex[:,1]**2)
angle = torch.atan2(spec_complex[:,1],spec_complex[:,0])