目录

Introduction

Clustering（聚类）

Dimension Reduction（降维）

 PCA（Principle component analysis，主成分分析）

Word Embedding（词嵌入）

Matrix Factorization(矩阵分解)

Introduction

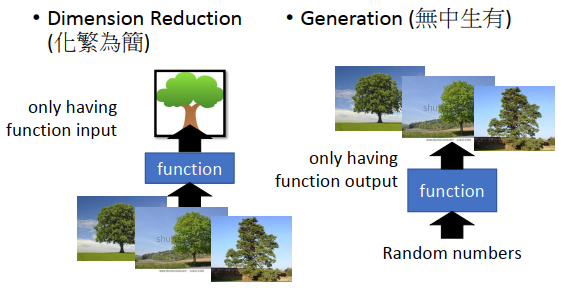
 无监督学习化繁为简聚类(Clustering)降维(Dimension Reduction)无中生有

1. 化繁为简就是把复杂的input变成比较简单的output，比如把一大堆没有打上label的树图片转变为一棵抽象的树。
2. 无中生有就是随机给function一个数字，它就会生成不同的图像。

Clustering（聚类）

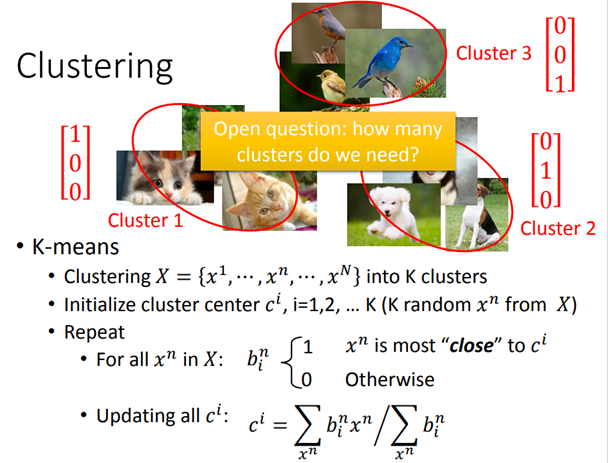
聚类，顾名思义，就是把相近的样本划分为同一类，比如对下面这些没有标签的image进行分类，手动打上cluster 1、cluster 2、cluster 3的标签，这个分类过程就是化繁为简的过程。一个关键的问题是，需要分几个cluster。

最常用的方法是K-means：

1. 有一大堆的unlabeled data，把它划分为K个cluster。
2. 从训练数据里随机找K个对象出来作为K个center ci的初始值。
3. 对所有数据，决定属于哪一个cluster，假设xn和ci最接近，那么xn就属于ci，用 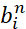表示。
4. 更新center：把每个cluster里的所有object取平均值作为新的center值。
5. 重复以上操作。

 HAC（Hierarchical Agglomerative Clustering，层次聚类）

• build a tree:

1. 对5个样本点两两计算相似度，挑出最相似的一对，比如样本点1和2；
2. 将样本点1和2进行merge (可以对两个vector取平均)，生成代表这两个样本点的新结点。
3. 此时只剩下4个结点，再重复上述步骤进行样本点的合并，直到只剩下一个root结点。

• pick a threshold：

选取阈值，构造好的tree上横着切一刀，相连的叶结点属于同一个cluster。

 HAC和K-means最大的区别在于如何决定cluster的数量，在K-means里，K的值是要你直接决定的；而在HAC里，你并不需要直接决定分多少cluster，而是去决定这一刀切在树的哪里。

Dimension Reduction（降维）

clustering的缺点是以偏概全，它强迫每个object都要属于某个cluster。如果把它强制归为某个cluster，就会失去很多信息；我们应该用一个vector来描述该object，这个vector的每一维都代表object的某种属性，这种做法就叫做Dimension Reduction。

• Why Dimension Reduction Help?

假设data为下图左侧中的3D螺旋式分布，用3D的空间来描述这些data其实是很浪费的，因为完全可以把这个卷摊平，此时只需要用2D的空间就可以描述这个3D的信息。

 如果以MNIST(手写数字集)为例，每一张image都是28*28的dimension，但是大多数28*28 dimension的vector转成image，看起来都不会像是一个数字，所以描述数字所需要的dimension可能远比28*28要来得少。

• How to do Dimension Reduction？

最简单的方法是Feature Selection，即直接从原有的dimension里拿掉一些直观上就对结果没有影响的dimension，就做到了降维。但这个方法不是总有用，因为很多情况下任何一个dimension其实都不能被拿掉，就像下图中的螺旋卷。

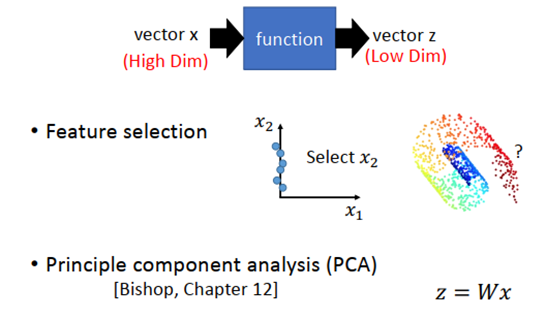
 PCA（Principle component analysis，主成分分析）

假设降维函数是一个linear function，，而PCA要做的就是根据很多个x找出W。

• PCA for 1-D

假设z是1维的vector，也就是把x投影到一维空间，我们希望所有x在W方向上投影得到的所有z分布越大越好，也就是说在投影之后不同样本之间的区别仍然是可以被看得出来的，所以投影结果的variance越大越好。

• 

• PCA for n-D
• 当然还可以投影到更高维的空间。其中wi必须相互正交，如果不加以约束，则找到的w1、w2…则是相同的。

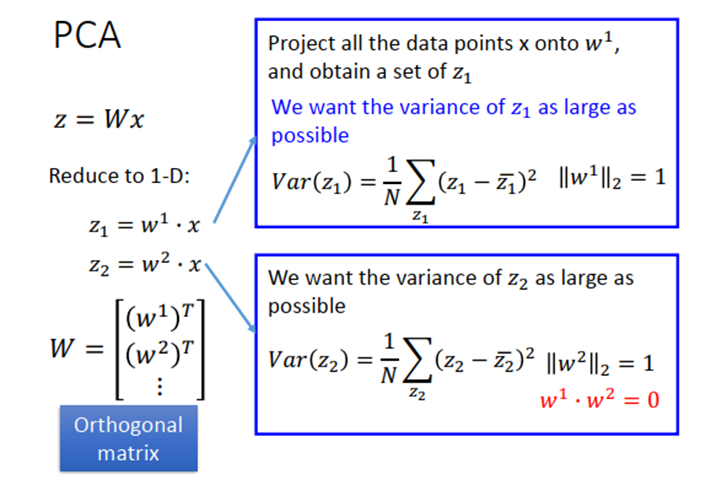
•  Lagrange multiplier

首先计算出z1 的均值，然后求出能使z1 方差最大的w1 ，但是有个约束条件w1 的二范数等于1，否则w1 就可以取无穷大。S是x的协方差矩阵，对称且半正定的（所有的特征值都是非负的）。

 现在问题转化成求一个w1 ，使得 最大。使用拉格朗日乘数法，利用目标和约束条件构造函数g(w1) ，然后g 对所有w 做偏微分等于0，得到Sw1=αw1 ，那么w1 就是S 的一个特征向量。经过化简得到 ，此时即求α 的最大值，也就是当S 的特征值α 最大时对应的那个特征向量w1  就是我们要找的目标。

结论：w1 是协方差矩阵S 中的特征向量，对应最大的特征值λ1 ​。

 如果计算w2 ，就是多了一个限制条件，w1 与w2 正交。

结论：w2 是协方差矩阵S 中的特征向量，对应第二大的特征值λ2 。

 PCA可以让降维后数据中不同dimension之间的covariance变为0，即降维后数据中不同feature之间是没有correlation的，这样的好处是减少feature之间的联系从而减少model所需的参数量。

如果把原来的input data通过PCA之后再给其他model使用，那这些model就可以使用简单的形式，而无需考虑不同dimension之间的交叉项，此时model得到简化，参数量大大降低，相同的data量可以得到更好的训练结果，从而避免overfitting的发生。

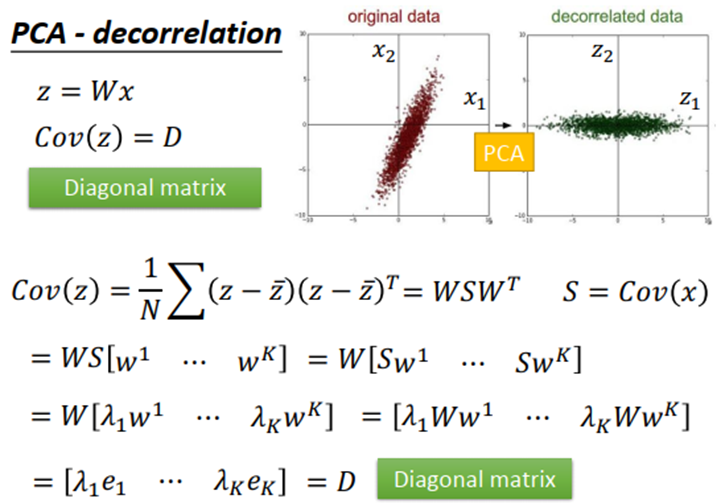
•  PCA – Another Point of View

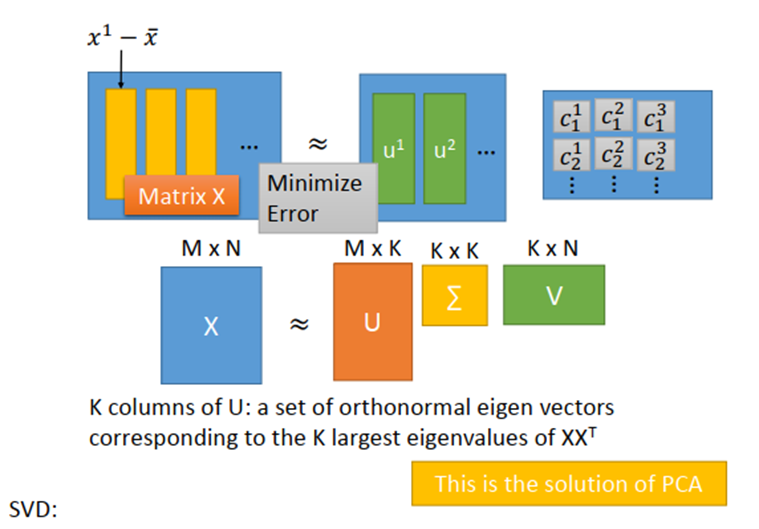
假设现在考虑手写数字识别，手写数字其实是由一些基本成分组成的，例如斜的直线，横的直线，比较长的直线，小圈、大圈等等。基本成分我们写作u1,u2,u3...，这些基本的成分其实就是一个一个的vector。以MNIST为例，不同的笔画都是一个28×28的vector，把这些基本成分vector加起来，得到的vector就代表了一个数字。写成公式如下图所示，其中x代表某一张图像的像素，x 是所有图像的平均。

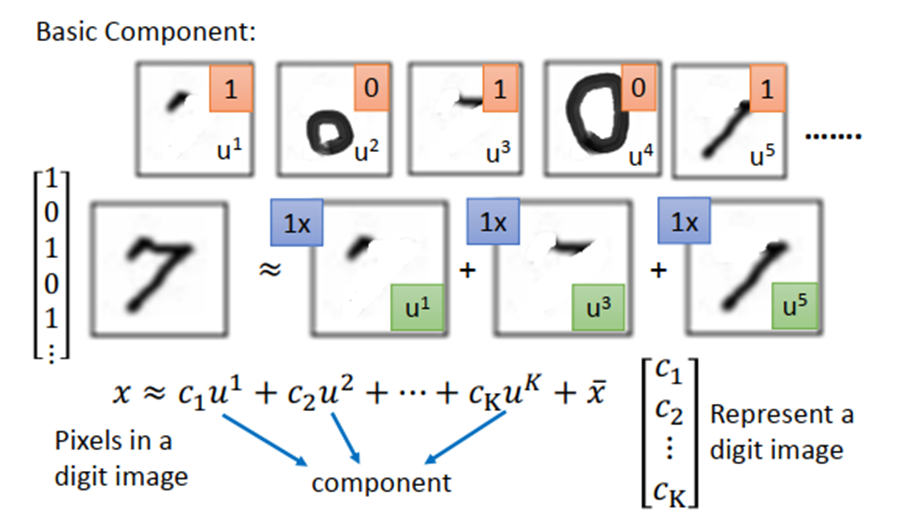
 简单证明如下：

目标是最小化左边矩阵X和右边相乘得到的矩阵之间的误差。

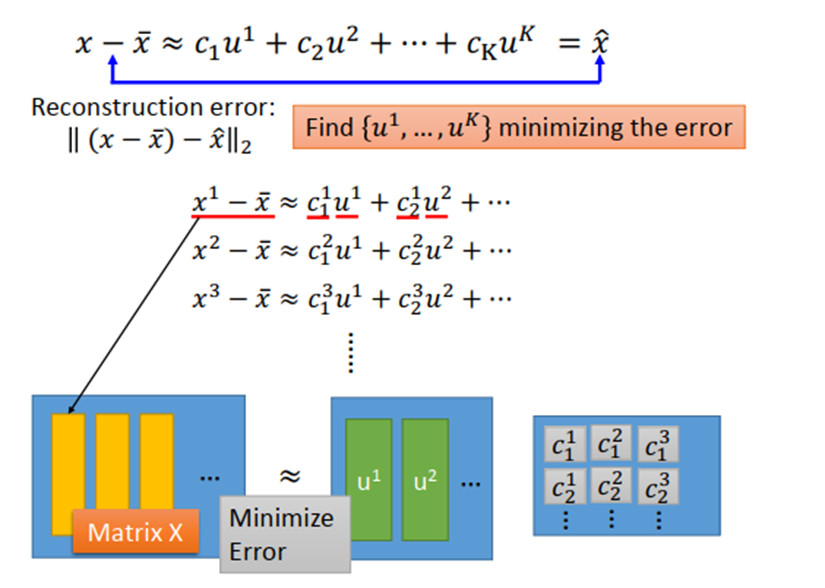
可以使用SVD将X分解成U,Σ,V。用奇异值分解的矩阵拆解方法，拆出来的3个矩阵相乘，跟左边矩阵X是最接近的。根据SVD的结论，组成矩阵U的k个列向量(标准正交向量)就是 最大的k个特征值(eignvalue)所对应的特征向量(eigenvector)，而 实际上就是x的协方差矩阵，因此U就是PCA的k个解。

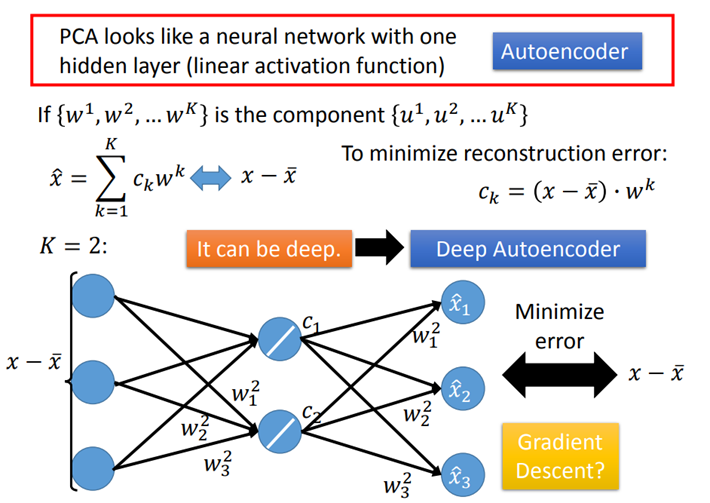
•  NN for PCA

1. 在linear的情况下，直接用PCA找WW远比用神经网络的方式更快速方便。
2. 用NN的好处是，它可以使用不止一层hidden layer，它可以做deep autoencoder。

•  Weakness of PCA

它是unsupervised的，如果我们要将下图绿色的点投影到一维空间上，PCA给出的从左上到右下的划分很有可能使原本属于蓝色和橙色的两个class的点被merge在一起。而LDA则是考虑了labeled data之后进行降维的一种方式，但属于supervised。

它是linear的，对于下图中的彩色曲面，我们期望把它平铺拉直进行降维，但这是一个non-linear的投影转换，PCA无法做到这件事情，PCA只能做到把这个曲面打扁压在平面上，类似下图，而无法把它拉开。对类似曲面空间的降维投影，需要用到non-linear transformation。

• PCA for Pokemon

有800种宝可梦，每种宝可梦可以用6个特征来表示。所以每个宝可梦就是6维的数据点，6维向量。接下来的问题是，我们要投影到多少维的空间上？如果做可视化分析的话，投影到二维或三维平面可以方便观察。

实际上，我们可以先找出6个特征向量和对应的特征值，并计算每个特征值比例，那第5、6个主成分的作用比较小，意味着投影数据的方差很小，宝可梦的特性在这两个主成分上信息很少，则分析宝可梦特性只需要前4个主成分。

PCA后选择4个主成分，每个主成分是一个6维向量（因为原来每个特征都要投影，那就有6种投影数据）。

对于PC1来说，每个值都是正的，因此这个principle component在某种程度上代表了宝可梦的强度。

• PCA for MNIST

对于手写字符识别来说，可以把每一张数字图像拆成成分的线性组合，每一个成分也是一张图像，通过PCA画出前30个成分，白色的地方代表有笔画。用这些成分做线性组合，就可以得到0-9的数字。

• PCA for Face

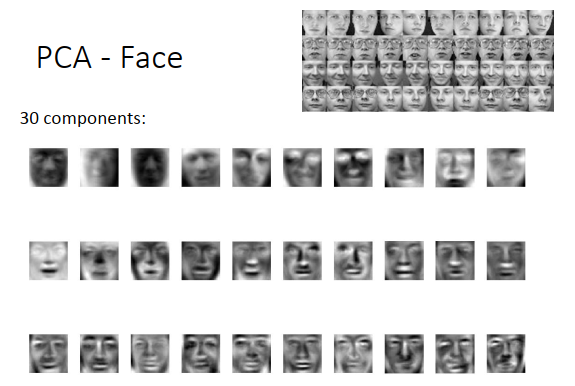
同理，通过PCA找出人脸的前30个组件(维度)，用这些脸的组件做线性组合就可以得到所有的脸。

• What happens to PCA

在对MNIST和Face的PCA结果展示的时候，找到的component好像并不算是component，比如MNIST找到的几乎是完整的数字雏形，而Face找到的也几乎是完整的人脸雏形。这是因为，weight ai 可以是正的也可以是负的，这会导致你找出来的component不是基础的组件，但是通过这些组件的加加减减肯定可以获得基础的组件元素。

• NMF(non-negative matrix factorization，非负矩阵分解)

如果想要得到类似笔画这样的基础component，就要使用NMF。NMF的基本精神是，强迫使所有组件和它的加权值都必须是正的，也就是说所有图像都必须由组件叠加得到。

Word Embedding（词嵌入）

词嵌入(Word Embedding)是降维算法(Dimension Reduction)的典型应用。

如果要用一个向量表示一个词，最典型的做法是1-of-N encoding。但这会导致任意两个vector都是不一样的，无法建立起同类word之间的联系。

还可以把有同样性质的word进行聚类(clustering)，划分成多个class，然后用word所属的class来表示这个word，但光做clustering是不够的，不同class之间关联依旧无法被有效地表达出来。

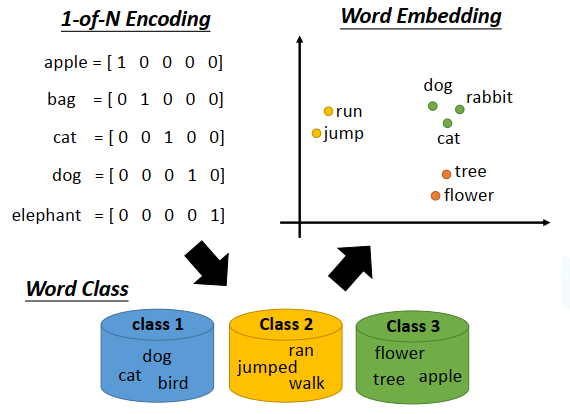
所以我们需要的是word embedding，把每一个word都投影到高维空间上，当然这个空间的维度要远比1-of-N Encoding的维度低，假如后者有10w维，那前者只需要50-100维就够了。从上图可以看出，类似语义的word更加接近。而且word embedding的每一维，可能都有特别的含义。

word embedding是一个无监督的方法，只要让机器阅读大量的文章，它就可以知道每一个词汇embedding之后的特征向量应该长什么样子。

我们的任务就是训练一个neural network，input是词汇，output则是它所对应的word embedding vector，实际训练的时候我们只有data的input，该如何解这类问题呢？

之前提到过一种基于神经网络的降维方法，叫做Auto-encoder，就是训练一个model，让它的输入等于输出，隐藏层拿出来就是降维的结果。但这里没法使用Auto-encoder，因为输入的向量通常是1-of-N编码，各维无关，很难通过自编码的过程学习出共有的特性。

Word embedding的基本精神就是，每一个词汇的含义都可以根据它的上下文来得到。比如机器在两个不同的地方阅读到了“马英九520宣誓就职”、“蔡英文520宣誓就职”，它就会发现“马英九”和“蔡英文”前后都有类似的文字内容，于是机器就可以推测“马英九”和“蔡英文”这两个词汇代表了可能有同样地位的东西，即使它并不知道这两个词汇是人名。

Word Embedding有两种做法：Count based与Prediction based。

• Count based

如果有两个词汇在文章中常常同时出现，则它们的词向量就会比较接近。这种方法一个代表性的例子是Glove vector。方法的原理是计算两个词向量的内积，使之与这两个词汇同时出现的次数相近。

• Prediction based

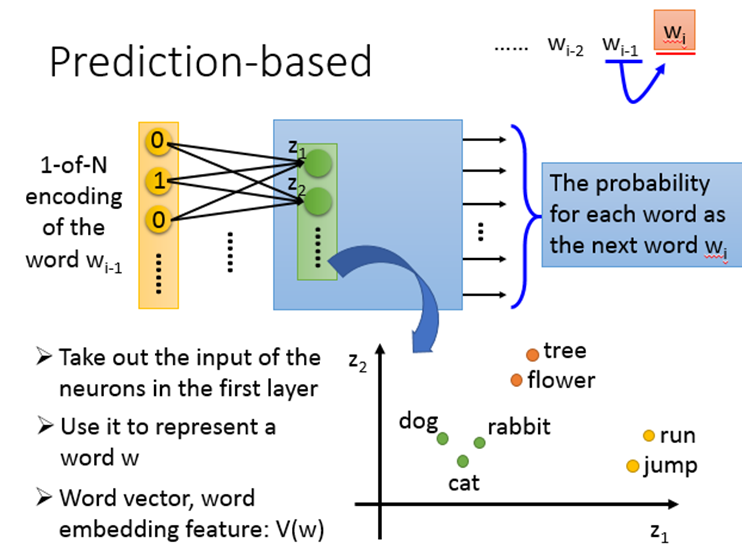
给定一个sentence，训练一个Neural network。它要根据当前的wordwi-1 预测下一个wordwi 是什么。我们把每个词汇用1-of-N encoding表示成一个特征向量，那么NN的input就是wi-1 的1-of-N encoding向量，output就是wi 为某个词汇的概率。

把第一个hidden layer的input拿出来，它们所组成的Z就是word的另一种表示方式，当我们input不同的词汇，向量Z就会发生变化。

•  Prediction作用原理

在训练model的时候，不管input是“蔡英文”还是“马英九”，都希望学习出来的结果是“宣誓就职”的概率比较大。为了使这两个不同的input通过NN能得到相同的output，就必须在进入hidden layer之前，就通过weight的转换将这两个input vector投影到位置相近的低维空间上。也就是说，尽管两个input vector作为1-of-N编码看起来完全不同，但经过参数的转换，将两者都降维到某一个空间中，在这个空间里，经过转换后的new vector 1和vector 2是非常接近的，因此它们同时进入一系列的hidden layer，最终输出时得到的output是相同的。

总结来讲，对word的1-of-N编码进行Word Embedding的结果就是神经网络第一个隐藏层的输入向量[z1,z2,…]T ，该向量考虑了word的上下文，我们可以通过控制第一个隐藏层的大小从而控制word降维空间的维数。

•  Sharing Parameters

只通过一个word预测下一个word太难了，因为word的搭配太多。因此可以使用更多的word去预测下一个word。这里用2个词汇作为例子，我们希望wi-2 与wi-1 相同dimension对应到第一层hidden layer相同neuron之间的连线拥有相同的weight。如果我们不这么做，那把同一个word放在不同的位置得到的结果就不一样。除此之外，这么做还可以通过共享参数的方式有效地减少参数量。

 用公式表示为 ，令 ，则 ，因此，只要我们得到了这组参数W，就可以与1-of-N编码x相乘得到word embedding的结果z。

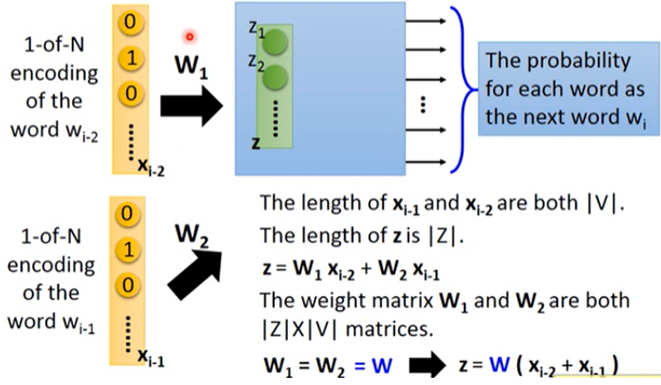
 那我们如何保证W1 和W2 一样呢？

首先在训练的时候就要给它们一样的初始值，然后在更新参数的时候减去相同的值。

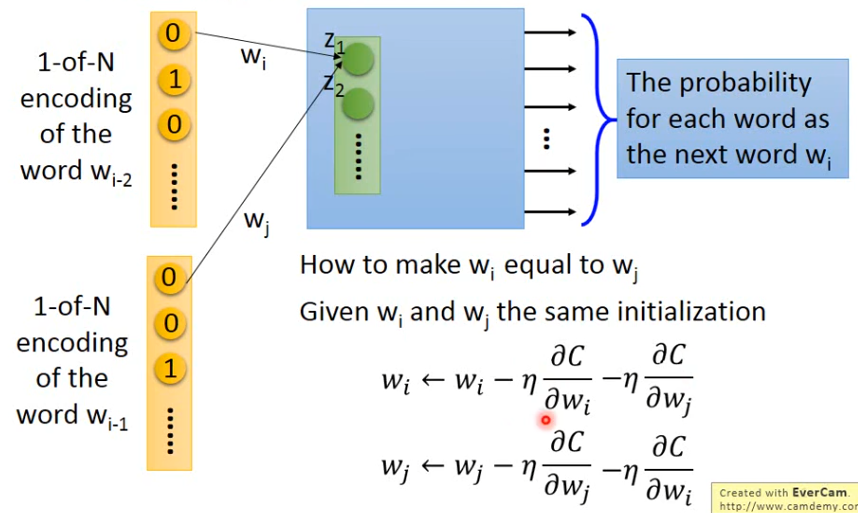
那么如何训练这个神经网络呢？这个神经网络完全是无监督，只要收集一大堆文字数据，然后训练。

除了上面的基本形态，Prediction-based方法还可以有多种变形。

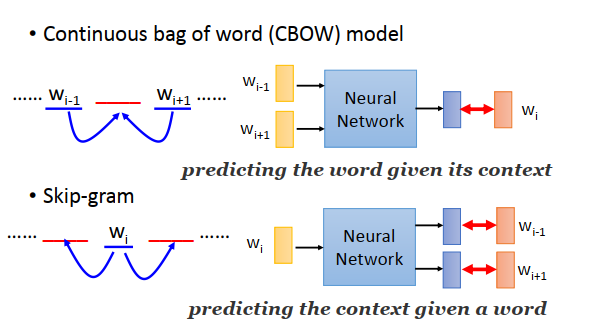
CBOW(Continuous bag of word model)：拿前后的词汇去预测中间的词汇。

Skip-gram：拿中间的词汇去预测前后的词汇。

Matrix Factorization(矩阵分解)

Matrix Factorization的思想是：有时候存在两种object，它们之间会受到某种共同的未知的潜在因素的操控，如果我们找出这些潜在因素，就可以对用户的行为进行预测，这也是推荐系统常用的方法之一。

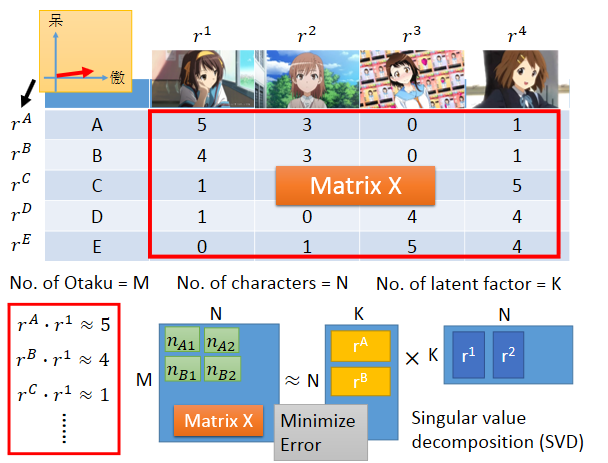
假设我们调查每个人购买的公仔数目，ABCDE代表5个人，每个人或者每个公仔实际上都是有着傲娇的属性或天然呆的属性，我们可以用vector去描述人和公仔的属性，如果某个人的属性和某个公仔的属性是match的，即他们背后的vector很像(内积值很大)，这个人就会偏向于拥有更多这种类型的公仔。

我们可以把购买的公仔数量合起来看做是一个矩阵X ，行数是人的数量，列数是公仔角色的数量。我们要做的事情就是找一组rA到rE，找一组r1到r4 ，让两个矩阵相乘后和矩阵X越接近越好，就是最小化重构误差。这个就可以用SVD求解。

如果X中缺少部分information，就难以用SVD精确描述，这时可以使用梯度下降求解，损失函数L，这个方法的关键之处在于计算上式时可以忽略那些缺少的数据，最终通过梯度下降求得ri和rj的值。

假设潜在因素的数量是2，可以发现A、B属于同一组属性，C、D、E属于同一种属性。动漫人物1和2属于同一组属性，动漫人物3和4属于同一组属性。结合动漫角色，可以分析出动漫角色的第一个维度是天然呆属性，第二个维度是傲娇属性。接下来就可以预测未知的值，只需要将人和动漫角色的vector做内积即可。

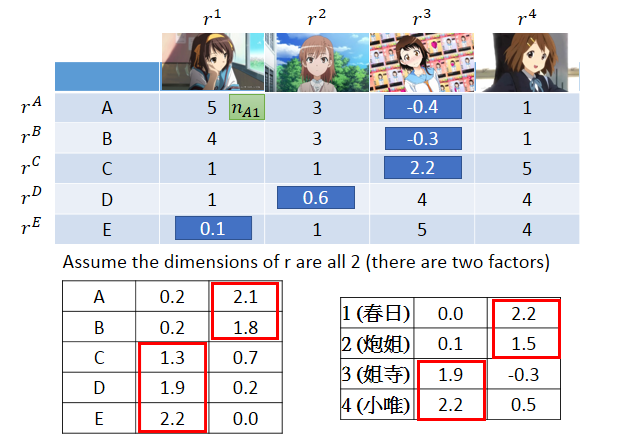
但是事实上，可能还会有其他因素操控这些数值，我们可以将式子更精确地改写成下图所示。

如果把matrix factorization的方法用在topic analysis（主题分析）上，就叫做LSA(Latent semantic analysis)，潜在语义分析。

Application

• 机器问答

把word vector两两相减，再投影到下图中的二维平面上，如果某两个word之间有类似包含于的相同关系，它们就会被投影到同一块区域。

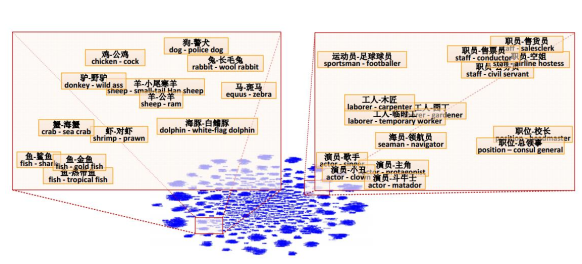
用词向量的概念，可以做一些简单的推论。如果有人问你，罗马之于意大利就好像柏林之于什么，那么机器就可以回答这种问题了。

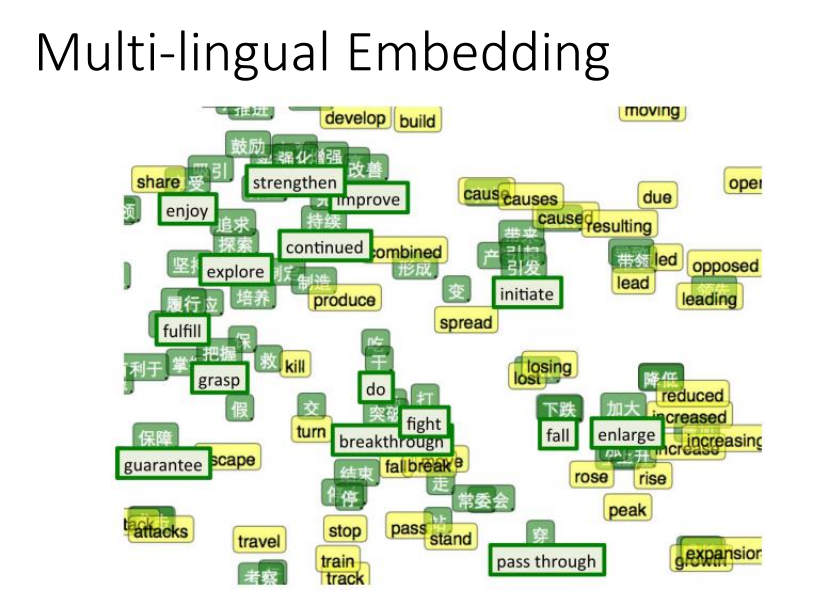
• Multi-lingual Embedding（多语言嵌入）

word vector还可以建立起不同语言之间的联系。如果你知道某些中文词汇和英文词汇的对应关系，你可以先分别获取它们的word vector，然后再去训练一个模型，把具有相同含义的中英文词汇投影到新空间上的同一个点接下来遇到未知的新词汇，无论是中文还是英文，你都可以采用同样的方式将其投影到新空间，就可以自动做到类似翻译的效果。

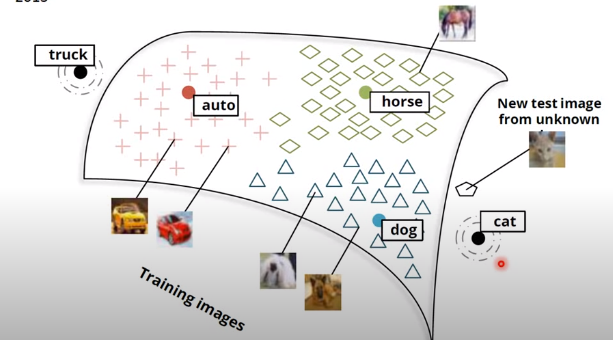
• Multi-domain Embedding（多域嵌入）

假设你已经得到horse、cat和dog这些词汇的vector在空间上的分布情况，你就可以去训练一个模型，把一些已知的horse、cat和dog图片去投影到和对应词汇相同的空间区域上。训练好这个模型之后，输入新的未知图像，根据投影之后的位置所对应的word vector，就可以判断它所属的类别。

• Document Embedding（文档嵌入）

除了Word Embedding，我们还可以对Document做Embedding。最简单的方法是把document变成bag-of-word，然后用Auto-encoder就可以得到该文档的语义嵌入(Semantic Embedding)，但光这么做是不够的。词汇的顺序代表了很重要的含义，两句词汇相同但语序不同的话可能会有完全不同的含义。