LeetCode583. 两个字符串的删除操作
动态规划五部曲:
1,确定dp数组(dp table)以及下标的含义:dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。
2,确定递推公式
- 当word1[i - 1] 与 word2[j - 1]相同的时候
- 当word1[i - 1] 与 word2[j - 1]不相同的时候
当word1[i - 1] 与 word2[j - 1]相同的时候,dp[i][j] = dp[i - 1][j - 1];
当word1[i - 1] 与 word2[j - 1]不相同的时候,有三种情况:
情况一:删word1[i - 1],最少操作次数为dp[i - 1][j] + 1
情况二:删word2[j - 1],最少操作次数为dp[i][j - 1] + 1
情况三:同时删word1[i - 1]和word2[j - 1],操作的最少次数为dp[i - 1][j - 1] + 2
那最后当然是取最小值,所以当word1[i - 1] 与 word2[j - 1]不相同的时候,递推公式:dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});因为 dp[i][j - 1] + 1 = dp[i - 1][j - 1] + 2,所以递推公式可简化为:dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1);
3,dp数组如何初始化:从递推公式中,可以看出来,dp[i][0] 和 dp[0][j]是一定要初始化的。dp[i][0]:word2为空字符串,以i-1为结尾的字符串word1要删除多少个元素,才能和word2相同呢,很明显dp[i][0] = i。
4,确定遍历顺序:从递推公式 dp[i][j] = min(dp[i - 1][j - 1] + 2, min(dp[i - 1][j], dp[i][j - 1]) + 1); 和dp[i][j] = dp[i - 1][j - 1]可以看出dp[i][j]都是根据左上方、正上方、正左方推出来的。所以遍历的时候一定是从上到下,从左到右,这样保证dp[i][j]可以根据之前计算出来的数值进行计算。
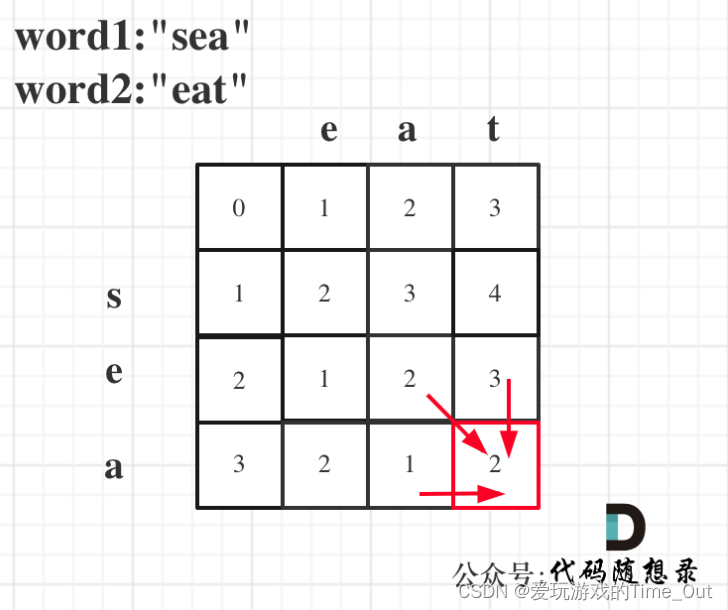
5,举例推导dp数组:以word1:"sea",word2:"eat"为例,推导dp数组状态图如下:
Java代码如下:
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return len1 + len2 - dp[len1][len2] * 2;
} 
LeetCode72. 编辑距离
动态规划五部曲:
1,确定dp数组(dp table)以及下标的含义:dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。
2,确定递推公式:在确定递推公式的时候,首先要考虑清楚编辑的几种操作,整理如下:
if (word1[i - 1] == word2[j - 1])
不操作
if (word1[i - 1] != word2[j - 1])
增
删
换也就是如上4种情况。
if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑,dp[i][j] 就应该是 dp[i - 1][j - 1],即dp[i][j] = dp[i - 1][j - 1];
为啥要即dp[i][j] = dp[i - 1][j - 1]呢?
那么就在回顾上面讲过的dp[i][j]的定义,word1[i - 1] 与 word2[j - 1]相等了,那么就不用编辑了,以下标i-2为结尾的字符串word1和以下标j-2为结尾的字符串word2的最近编辑距离dp[i - 1][j - 1]就是 dp[i][j]了。
在整个动规的过程中,最为关键就是正确理解dp[i][j]的定义!
if (word1[i - 1] != word2[j - 1]),此时就需要编辑了,如何编辑呢?
- 操作一:word1删除一个元素,那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i - 1][j] + 1;
- 操作二:word2删除一个元素,那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。
即 dp[i][j] = dp[i][j - 1] + 1;
怎么都是删除元素,添加元素去哪了。
word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样! dp数组如下图所示意的:
a a d
+-----+-----+ +-----+-----+-----+
| 0 | 1 | | 0 | 1 | 2 |
+-----+-----+ ===> +-----+-----+-----+
a | 1 | 0 | a | 1 | 0 | 1 |
+-----+-----+ +-----+-----+-----+
d | 2 | 1 |
+-----+-----+ 操作三:替换元素,word1替换word1[i - 1],使其与word2[j - 1]相同,此时不用增删加元素。
可以回顾一下,if (word1[i - 1] == word2[j - 1])的时候我们的操作 是 dp[i][j] = dp[i - 1][j - 1] 对吧。
那么只需要一次替换的操作,就可以让 word1[i - 1] 和 word2[j - 1] 相同。
所以 dp[i][j] = dp[i - 1][j - 1] + 1;
综上,当 if (word1[i - 1] != word2[j - 1]) 时取最小的,即:dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
3,dp数组如何初始化:再回顾一下dp[i][j]的定义:dp[i][j] 表示以下标i-1为结尾的字符串word1,和以下标j-1为结尾的字符串word2,最近编辑距离为dp[i][j]。那么dp[i][0] 和 dp[0][j] 表示什么呢?dp[i][0] :以下标i-1为结尾的字符串word1,和空字符串word2,最近编辑距离为dp[i][0]。那么dp[i][0]就应该是i,对word1里的元素全部做删除操作,即:dp[i][0] = i;同理dp[0][j] = j;
4,确定遍历顺序:
从如下四个递推公式:
dp[i][j] = dp[i - 1][j - 1]dp[i][j] = dp[i - 1][j - 1] + 1dp[i][j] = dp[i][j - 1] + 1dp[i][j] = dp[i - 1][j] + 1
可以看出dp[i][j]是依赖左方,上方和左上方元素的,如图:

所以在dp矩阵中一定是从左到右从上到下去遍历。
5,举例推导dp数组:以示例1为例,输入:word1 = "horse", word2 = "ros"为例,dp矩阵状态图如下:

Java代码如下:
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
dp[i][0] = i;
}
for (int j = 1; j <= n; j++) {
dp[0][j] = j;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
} else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i][j - 1]), dp[i - 1][j]) + 1;
}
}
}
return dp[m][n];
}