阅读 《Sensing prior constraints in deep neural networks for solving exploration geophysical problems dendrimers》

题目译为《深度神经网络中用于解决勘探地球物理问题的感知先验约束》

研究意义

该研究提出三种可能的策略，以有效地讲地质和/或地球物理约束纳入深度神经网络（DNNs）。相关策略有助于解决应用 DNNs 求解地球物理问题时通常面临的主要挑战，如泛化性差、可解释性弱和物理不一致。

研究内容

1. 通过地质和地球物理正向建模生成合成训练数据集，并将先验知识作为输入DNN的一部分进行适当编码，从而将约束集成到数据中。
2. 在DNN架构中设计物理算子和预处理器的不可解释的自定义层，以修改或塑造网络中计算的特征图，使其与先验知识一致。
3. 实现先验地质信息和地球物理定律，作为训练DNN的损失函数的正则化项。

研究背景

• 使用DNN面临的挑战：
  – 1、地球物理领域缺乏足够训练数据集，其中大多数现有数据都是未标记的。现场数据的有限可用标签往往时高度主观或有偏见的，因为标签常常时未知或不可靠的。训练数据集的标签不足和不准确限制了DNN的性能。
  – 2、训练后的DNN所应用的现场地球物理数据的多样性。简单说就是输入训练后的DNN模型的地球物理现场数据可能与训练数据有很大不同。这导致了训练的DNN模型的可推广性较差。
  – 3. 可解释性低和物理一致性差。这些源于DNN的常见理论弱点，由于地球物理数据的高度复杂性和不确定性，在地球物理应用中可能会被放大。

对DNN施加领域知识约束（先验地质信息和/或地球物理定律）是提高模型可推广性、可解释性和物理一致性的一种潜在方法。

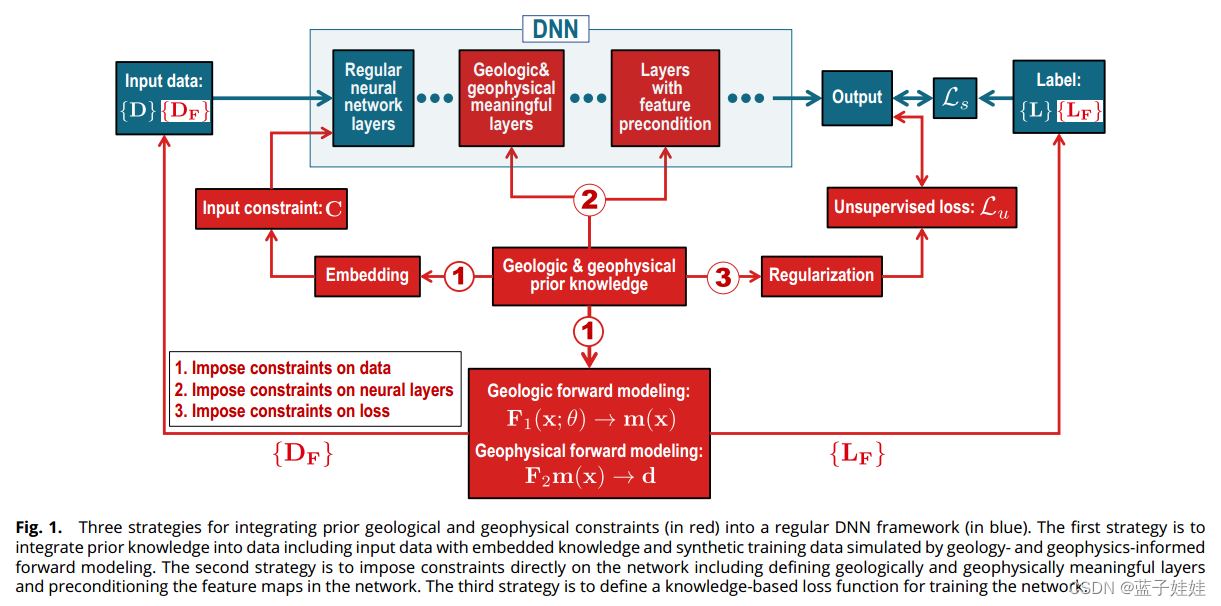
对数据施加约束

通过将先验知识或预期特征嵌入到训练或输入数据中，有效地对DNN施加先验约束。

解决缺乏标记的训练数据的这一挑战的一种方法是通过使用各种数值地质和地球物理正向建模方法生成带有标签的合成训练数据集。

该方法地面实况自动生成，无需人工标记。该方法是灵活的，建模参数是随机选择的，以生成不同特征的大量训练数据集。这里将正向建模视为一种将先验知识嵌入训练数据集中的方法，然后将其用于训练DNN以从数据集中提取嵌入的知识，期望这种训练的DNN类似于合成数据的现场数据中提取类似的知识。

首先进行数值地质正演模型，得到数字地质模型 $\mathbf{m}(\mathbf{x})$，表示为：
$$\mathbf{m}(\mathbf{x})={\mathbf{F}}_1(\mathbf{x},{\theta }_1),$$
其中，$\mathbf{x}$ 表示模型空间，${\mathbf{F}}_1$ 表示地质正向过程，如地层，河道和构造正向建模。正向模拟过程 ${\mathbf{F}}_1$ 通常是利用地质的先验知识精心制定的算子或方程。${\theta }_1$ 表示从所有可能的选项中随机选择的一组建模参数，以生成许多不同的模型。通过正向建模，将各种地质性质或特征嵌入模型中。模型空间中感兴趣的地质特征或信息的标签，如沉积相、河道相、层位和断层，可以自动定义。这些地质标签 { L F } \{\mathbf{L}_{\mathbf{F}}\} {LF​}，如下图所示的紫色框所示。

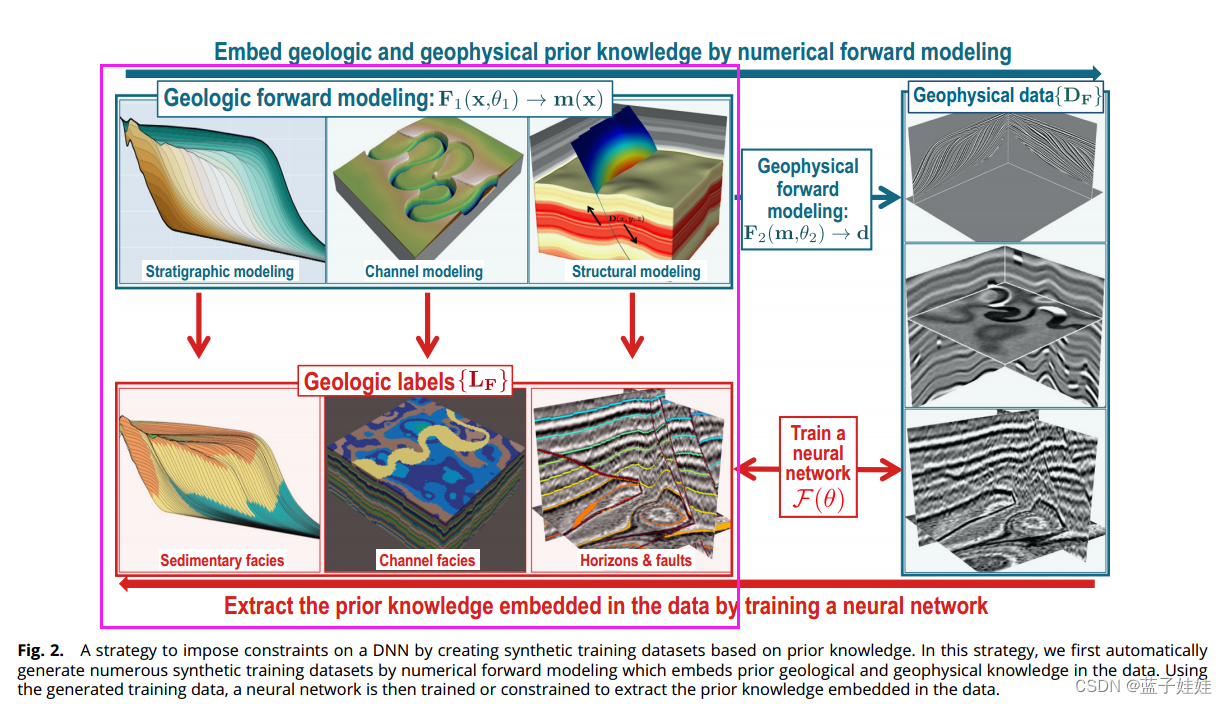
模拟的地质模型可以转换为地球物理特性的模型，例如密度、速度和阻抗。因此，使用模拟模型 $\mathbf{m}$，我们可以进行地球物理正演建模来模拟地球物理数据 $\mathbf{d}$，表示为
$$\mathbf{d}={\mathbf{F}}_2(\mathbf{m},{\theta }_2),$$
其中${\mathbf{F}}_2$ 表示地球物理正向建模过程或算子，例如波传播和卷积，${\theta }_2$ 表示从所有可能的选项中随机选择的一组建模参数，以生成大量且多样的地球物理数据 { D F } \{ \mathbf{D}_{\mathbf{F}}\} {DF​}。如下图所示的右侧面板所示的模拟地球物理数据，通过将反射率模型与Ricker小波卷积计算的3D地震图像。这三幅图像从上到下分别包含地层几何形状，河道特征以及褶皱和断层构造的地质意义信息。这些图像特征对应于用于模拟图像的地质模型中嵌入的地质知识（如下图中左下角的地质标签）。目标是使用一对训练数据集 { D F } \{\mathbf{D}_{\mathbf{F}}\} {DF​} 和 { L F } \{\mathbf{L}_{\mathbf{F}}\} {LF​} 来训练DNN，该DNN可以自动准确地提取嵌入地球物理数据中的地质知识。

该工作流程主要分为两步：
(1) 用定义明确的方程或先验知识进行正向模拟以生成数据；
(2) 训练 DNN 以实现逆映射 $\mathcal{F}(\theta )$ 从生成的数据中获取知识。

$${\mathbf{F}}_1(\mathbf{x},{\theta }_1)\to \mathbf{m}(\mathbf{x})\to {\mathbf{F}}_2(\mathbf{m}(\mathbf{x}),{\theta }_2)\to \mathbf{d}\to \mathcal{F}(\theta )\to \tilde{\mathbf{m}}(\mathbf{x})$$

从地球物理数据中反演地质知识通常比正演过程更具有挑战性，有时很难用方程来定义。DNN 通过从大量训练数据集中学习，在统计上逼近这种复杂的映射方面非常强大。注意，训练数据的正向建模和 DNN 的训练过程可以同时执行，使得当训练收敛时可以自适应地停止数据生成。

有时可能使用 DNN 来近似地球物理正向建模以加速数据模拟。在这种情况下，我们不需要显示地生成数据来训练 DNN。相反，我们可以将物理正向建模作为 DNN 体系结构或训练循环的一部分，其中在损失函数中实现物理方程或算子，以作为训练 DNN 的物理监督。这实际上是一种经典的无监督学习或物理形成的神经网络。

由合成数据集训练的各种 DNN 模型已成功应用于解决多种地球物理问题，包括地震去噪、地震偏移、速度模型构建、阻抗反演和地震解释。如图3所示，由地球物理正向模拟生成的合成训练数据集已用于训练 DNN，以根据空间 ($x$)，时间 ($t$) 和偏移 ($o$) 域中记录的原始地震道集 $s(o;x,t)$ 直接建立速度模型 $\tilde{v}(x,z)$。在这些过程中，通过基于物理的正向建模，将先验领域知识（即速度模型和模拟数据之间的物理关系）嵌入到合成训练数据集中。

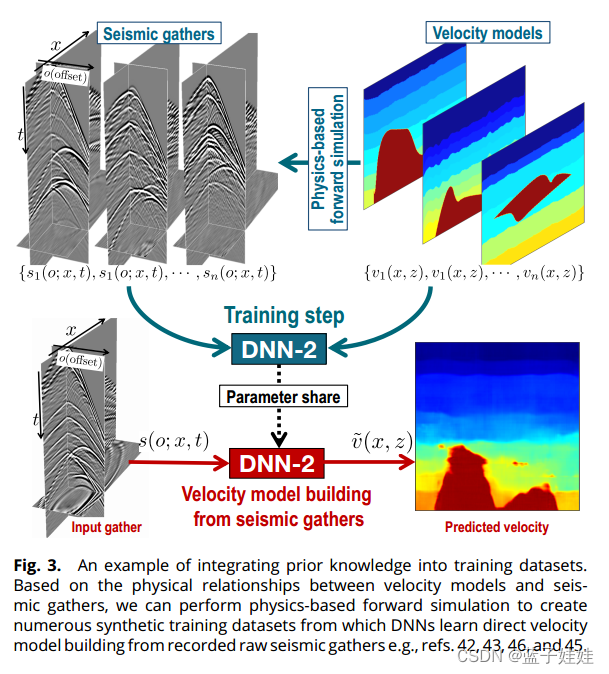
构造 DNN 是为了从训练数据集中学习，以推断从数据（相似立方体或地震道集）到速度模型的直接映射。这些方法提供了一种潜在的理想方法，可以从记录的地球物理数据中直接对地下进行成像，而无需像传统的地球物理成像工作流程中那样解决计算昂贵和不方便的反演问题。然而，它们很少被应用于复杂的现场实例，并取得令人满意的结果。这可能是因为合成训练数据集的大小和丰富性不足，并且现场示例在地质背景、数据采集（包括空间和时间分辨率、频率和调查几何形状）、噪声和处理误差方面可能与训练数据集有很大差异。提高合成训练数据集的多样性至关重要，一些作者建议使用生成对抗网络。

对数据施加约束的另一种方法是将先验知识或信息适当地嵌入或编码为可以直接馈送到 DNN 模型中的张量。该方法的优点是，我们可以在推理步骤中对 DNN 模型隐含地施加约束，以便在将模型应用于测试数据时有效地引入人类互动。一些作者已经表明，将先验信息，如地下结构特征、低频数据特征和初始速度模型输入 DNN 有助于提高其对地震全波形反演的鲁棒性。

在大多数地球科学问题中，必须通过整合逐渐更新的数据和先验知识来不断更新解决方案。深度学习提供了一种方便的方法来合并所有类型的输入数据和先验信息（可能来自各种来源和模态）以进行全面预测。将先验信息嵌入 DNNs 的输入是一种方便的手段，可以在推理步骤中对训练后的 DNN 施加约束或实现人类交互，以提高其可推广性，并获得地质或地球物理上合理的结果。此外，经过训练的 DNN 模型的推理步骤是高效的；我们可以通过修改模型的输入来快速甚至立即获得更新的结果。

---

将约束集成到网络中

之前讨论了将先验知识嵌入到训练或输入数据中是对 DNN 施加约束的有效方法。然而，在推理步骤中 DNN 的输出不能保证满足以这种方式施加的约束。提出了两种方法，通过定义自定义层和在 DNN 架构中利用先验知识实现特征预处理，对 DNN 施加硬约束。

将约束集成到网络中的一种更直接的方法是将先验知识预处理应用于在神经网络层中计算的特征图，特别是输出附近的解码器层。这种预处理可以使用平滑滤波器或任何其它算子来执行，以修改特征图中的值并使其与先验知识一致。

将约束条件集成到损失函数中

通过损失函数施加先验约束类似于在地球物理反演问题的目标函数中实现正则化项，它已被广泛研究，尤其在半监督和无监督学习以及物理告知神经网络 (PINN) 中。

缺乏标记的训练数据集是应用深度学习解决大多数地球科学问题的常见挑战。半监督或无监督学习是解决这一挑战的一种潜在方法，通过使用无监督损失函数来使用未标记的数据集和先验约束来训练 DNN。

图 S2 显示了半监督学习的简单框架，其中监督 (${\mathcal{L}}_s$) 和无监督 (${\mathcal{L}}_u$) 损失函数被联合用于优化网络参数。监督损失通常仅建立在一小部分标记数据的基础上。无监督损失基于先验知识或预测的一致性约束，将大量未标记数据集成到训练过程中，这对于训练更好的广义网络模型至关重要。当没有标签可用于监督时，监督损失缺失，这代是无监督的学习方法。已经提出了各种半监督和无监督的学习策略，它们通常在无监督损失函数的选择上有所不同。

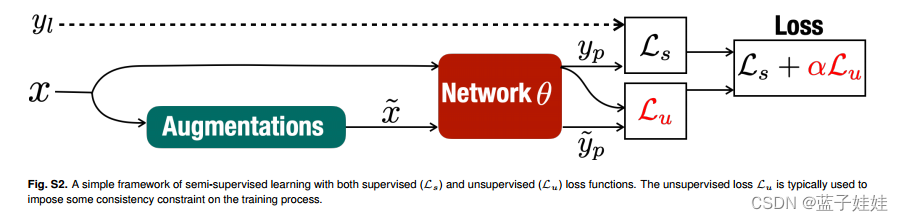
如图 S2 所示，损失函数被联合用于优化网络参数 $\theta$，表示为

$$\underset{\theta }{\min }\sum _{x\in X_L,y\in Y_L}{\mathcal{L}}_s(x,y;\theta )+\sum _{x\in X_U}{\mathcal{L}}_u(x,\tilde{x};\theta ).$$

其中，$X_L$ 表示具有标签 $Y_L$ 的数据的小子集，而 $X_U$ 表示没有标签的数据的大得多的子集。仅使用一小组标记数据通过最小化 ${\mathcal{L}}_s$ 来训练深度神经网络 ($\theta$) 可能很容易导致过拟合。无监督损失 (${\mathcal{L}}_u$) 基于预测的一些先验知识或一致性约束将大量未标记数据 $X_U$ 带入训练过程，这对于训练更好的广义网络模型至关重要。图 S2 显示了一种典型类型的一致性约束，其中由同一网络分别从 $x$ 及其扰动或增强版本 $\tilde{x}$ 计算的预测 $y_p$ 和 ${\tilde{y}}_p$ 应该是一致的。在这种情况下，${\mathcal{L}}_u$ 是预测 $y_p$ 和 ${\tilde{y}}_p$ 之间的差的测量值。应用于 $x$ 的增强可以是添加噪声、旋转、翻转、调整大小、计算属性等。对于旋转、翻转或调整大小的 $\tilde{x}$，我们需要在将预测 ${\tilde{y}}_p$ 与 $y_p$ 比较之前撤销其相应的增强。

半监督学习已被广泛用于解决地球物理问题。基于类似的想法，已经提出了物理引导和数据驱动的混合训练方案，以提高地球物理反演深度学习的稳健性和可推广性。在这些方案中，通过基于地球物理定律定义无监督损失 ${\mathcal{L}}_u$，将物理引导引入训练步骤。然而，它们与PINNs 的不同之处在于，它们不利于自动微分来计算损失中涉及的导数。无监督学习可以大仙未标记数据中的隐藏模式，也被用于各种任务，包括地震相分类、地震信号或波形分类，岩性分类、地震偏移和反演。

PINNs

通过损失函数将先验信息或约束强加给神经网络的另一种代表性方法是构建 PINN，并用基于支配物理定律（例如，偏微分方程 (PDE)）构建的物理形成的损失函数训练它们。通过最小化物理告知损失函数，可以训练 PINN 来估计支配物理定律的结果。尽管经过训练的网络通常不了解底层物理，但由于其普遍逼近和高表达能力，它们可以推断复杂控制物理方程的解空间。PINN 可以解决涉及偏微分方程的正问题和反问题，因此，已成为科学计算机器学习的热门话题。PINN 可以用各种网络架构构建，如全连接、递归和卷积神经网络。

图9的上部分显示了一个简单的 PINN，它是用全连接神经网络的架构实现的。该 PINN 框架由公共神经网络的第一部分和第二物理信息部分组成。

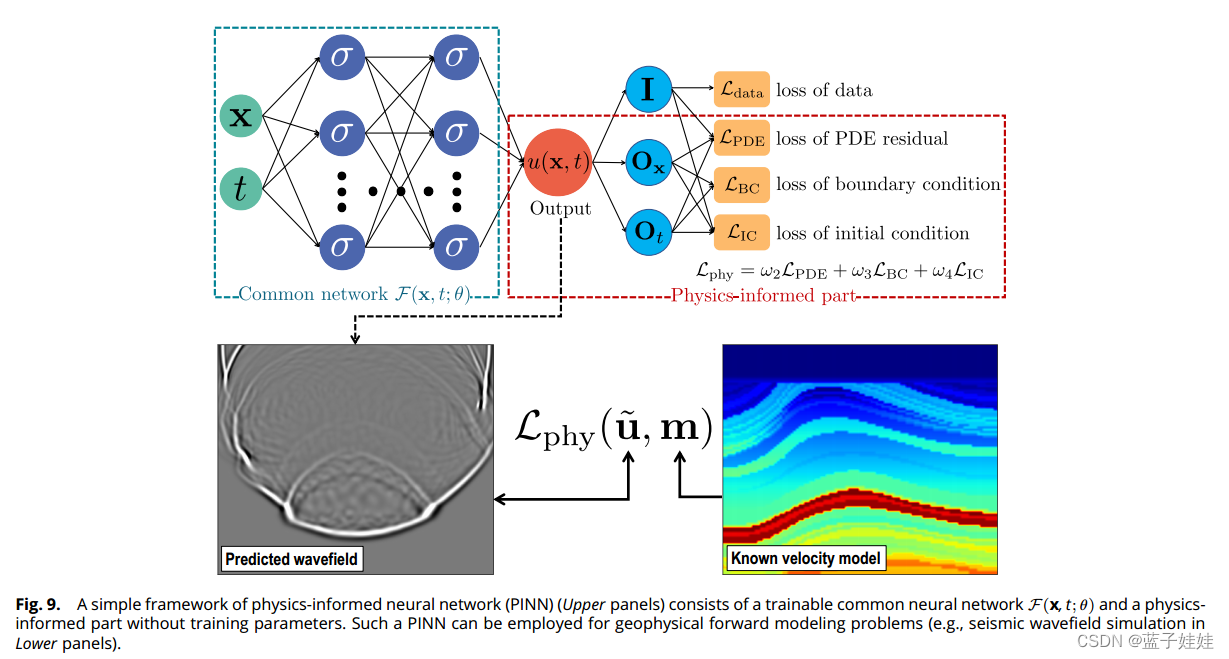
给定时间 $t$ 和空间坐标 $\mathbf{x}$，网络 $\mathcal{F}(\theta )$ 被训练来预测 $u(\mathbf{x},t)=\mathcal{F}(\mathbf{x},t;\theta )$，其通过最小化如下混合损失函数来满足测量数据和一些物理方程：
$$\underset{\theta }{\mathrm{argmin}}{\omega }_1{\mathcal{L}}_{\text{data}}(\mathbf{x},t;\theta )+{\omega }_2{\mathcal{L}}_{\text{PDE}}(\mathbf{x},t;\theta )+{\omega }_3{\mathcal{L}}_{\text{BC}}(\mathbf{x},t;\theta )+{\omega }_4{\mathcal{L}}_{\text{IC}}(\mathbf{x},t;\theta ).$$

在物理信息部分（在图9中的红色虚线框内），${\mathbf{O}}_{\mathbf{x}}$ 和 ${\mathbf{O}}_t$ 分别表示应用于关于空间坐标 $\mathbf{x}$ 和时间 $t$ 的预测 $u(\mathbf{x},t)$ 的物理算子。在偏微分方程中，这种算子由预定义的先验物理参数缩放的空间和时间导数（不训练）。在 PINN 中，导数是通过自动微分计算的，这提供了计算导数的准确方法，并避免了数值微分中出现的截断或舍入误差。$\mathbf{I}$ 表示同一算子，并且基于预测 $u(\mathbf{x},t)$ 与在一些特定时间和空间位置测量的数据之间的相似性或差异来定义数据损失 ${\mathcal{L}}_{\text{data}}$。损失 ${\mathcal{L}}_{\text{PDE}}$ 是由对预测 $u(\mathbf{x},t)$ 的运算 (${\mathbf{O}}_{\mathbf{x}}$ 和 ${\mathbf{O}}_t$) 的组合定义的支配 PDE 的残差。损失函数 ${\mathcal{L}}_{\text{BC}}$ 和 ${\mathcal{L}}_{\text{IC}}$ 分别强制预测的先验边界和初始条件。

三个物理知情损失函数 ${\mathcal{L}}_{\text{PDE}}$、${\mathcal{L}}_{\text{BC}}$ 和 ${\mathcal{L}}_{\text{IC}}$ 将先验控制物理方程、边界条件和初始条件的约束纳入训练过程，并确保预测或解满足先验约束。我们可以在没有任何标记数据的情况下仅使用物理知情损失函数来训练 PINN，这实际上也可以被视为一种无监督的训练策略。如果有一些测量数据或精心模拟的数据可用，我们可以通过数据损失 ${\mathcal{L}}_{\text{data}}$ 和物理信息损失来使用它们监督训练过程，这可以被视为半监督训练策略。这样的标记数据虽然是有限的，但有助于加快训练过程的收敛。

PINN 最近被探索用于解决地球物理正向建模和反演，这涉及到对偏微分方程的深入研究。以地震建模和反演为例，我们可以构建基于 PINN 的地球物理正演建模的基本框架（图9中的下部分）和反演。在正向建模中，训练神经网络（主要构造为全连接神经网络）来近似函数 $\mathcal{F}(\mathbf{x},t;\theta )$ 其可以直接且连续地预测在任意时间 $t$ 和空间位置 $\mathbf{x}$ 处的波场 $\tilde{\mathbf{u}}(\mathbf{x},t)$。基于地震波方程，将已知的速度模型 $\mathbf{m}(\mathbf{x})$ 与预测的波场 $\tilde{\mathbf{u}}(\mathbf{x},t)$ 一起用于构造用于训练网络的基于物理的损失函数 ${\mathcal{L}}_{\text{phy}}(\tilde{\mathbf{u}},\mathbf{m})$，直到波方程拟合或损失最小化收敛。在基于 PINN 的反演中，另一个神经网络 $\mathcal{F}(\mathbf{x},\theta )$ 可以被训练为直接推断速度模型 $ $\tilde{\mathbf{m}}(\mathbf{x})$，该速度模型在控制波方程下定义的损失函数 ${\mathcal{L}}_{\text{phy}}$ 最小化。在这种反演过程中，通常需要正演建模过程来模拟波在地下的传播，以公式化损失函数，类似于传统反演方案中所做的工作。因此，通常采用预训练的正向建模 PINN 来模拟波场数据 $\mathbf{u}$，该数据又被用于构造用于训练反演的 PINN 的损失 ${\mathcal{L}}_{\text{phy}}(\mathbf{u},\tilde{\mathbf{m}})$。考虑到正向建模过程总是与反演相耦合，一些作者建议通过公共损失函数将两个网络连接起来，共同训练两个 PINN，用于正向建模和反演。在这种情况下，用于在训练过程中更新它们的参数。

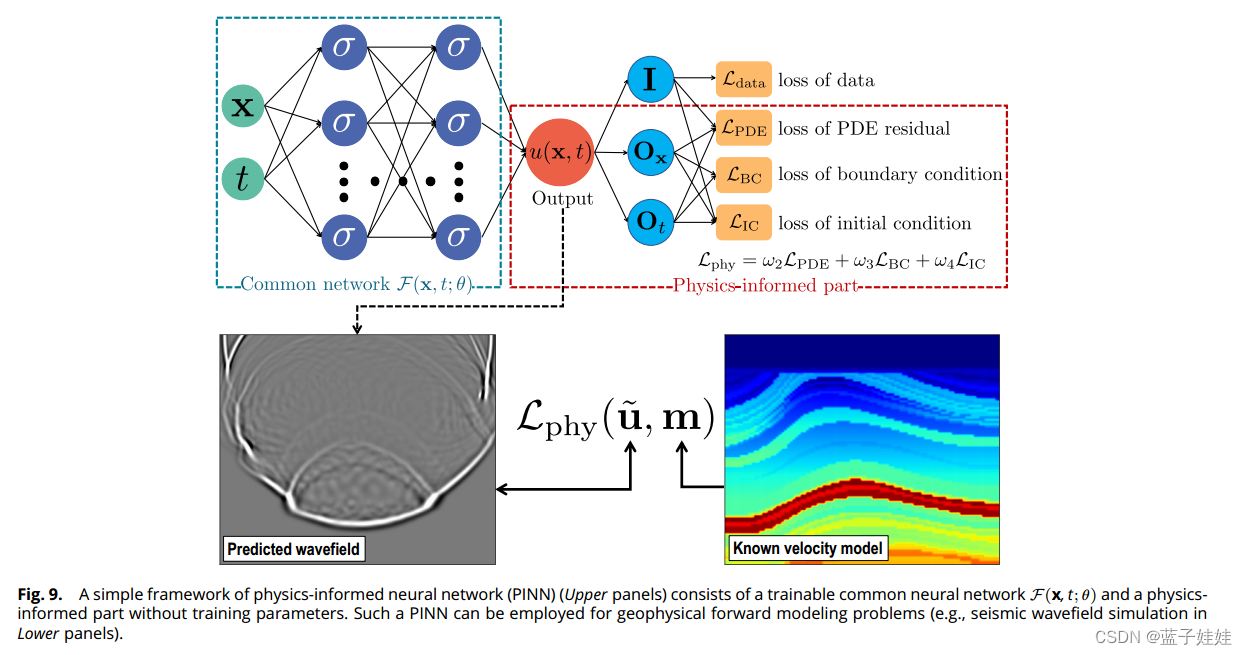
总之，PINN 提供了另一种合理的方法，通过基于物理方程构建物理知情损失函数来训练网络，从而对神经网络施加先验约束。在许多应用中已经证明，PINN 可以在有限甚至没有标记数据的情况下，以物理知情的方式有效学习控制方程的解。PINN 在解决 PDE 问题方面显示出一些优于传统方法的显著优势。首先，PINN 是一种无网格算法，能够避免由于基于网络的离散化而产生的截断和舍入误差，并且能够灵活地解决任意复杂几何域中的问题。其次，PINN 能够直接解决非线性和复杂问题，而不需要进行传统求解器通常需要的任何假设、线性化、简化或局部时间步进 (local time-stepping)。最后，相同的 PINN 框架可以用于联合求解正向和反向问题。

然而，基于 PINN 的地球物理正演建模和反演解决方案仍然存在局限性。首先，训练 PINN 非常棘手，计算成本也很高（它可能比传统的求解器更昂贵），尤其是在预测复杂的地球物理场和地球模型时。其次，为某个 PDE 预先训练的 PINN 很少能适应或推广到同一 PDE 的参数设置（例如，方程的物理变量、初始和边界条件）的变化，倾向于进行平滑的预测，因此通常很少恢复建模和回归结果中的细节或高频特征。