Tree of Thoughts: Deliberate Problem Solving with Large Language Models

概述：

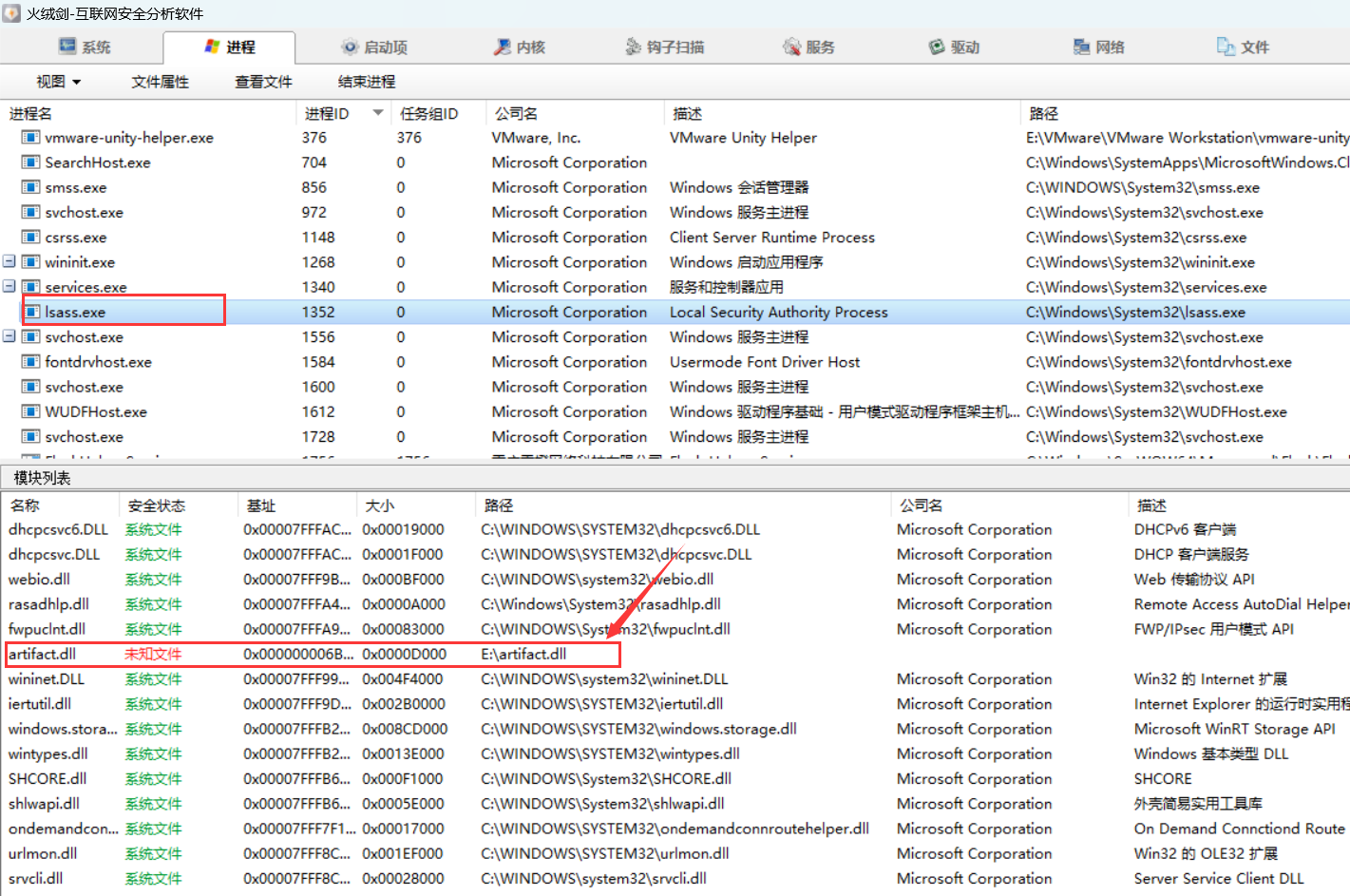
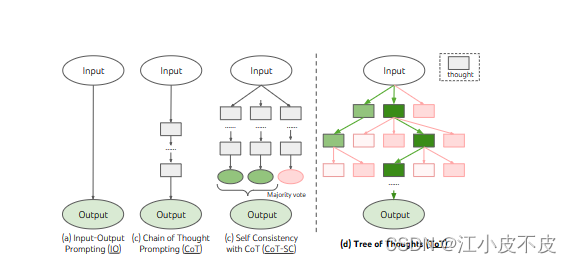
通过思维链（ToT） 允许 LM 通过考虑多个不同的推理路径和自我评估选择来决定下一个动作过程来执行深思熟虑的决策，以及在做出全局选择时展望未来或回溯

在24点游戏中，而具有思维链提示的 GPT-4 仅解决了4% 的任务，我们的方法的成功率为 74%。

核心思想：

一个真正的解决问题的过程涉及重复使用现有信息来启动探索，这反过来又披露了更多的信息，直到最终找到获得解决方案的方法。即通过树来进行搜索和回溯。

背景：

IO prompting

语言模型（LM）将输入x转换为输出y的常见方法

我们可以使用语言模型来将给定的输入x转换为相应的输出y。输入-输出提示是这种转换过程中最常见的方法之一。
promptIO (x)是一个用于封装输入x的任务指令和/或一些输入-输出示例的方式。它的目的是为了帮助语言模型理解并生成适当的输出。

CoT

coT用于解决输入x到输出y的映射问题，尤其是当x是一个数学问题而y是最终的数值答案时。关键思想是引入思想链z1，···，zn来连接x和y。

当x是一个数学问题而y是最终的数值答案时。关键思想是引入思想链z1，····，zn来连接x和y。从数学上来理解就是每个思想zi可以表示为数学QA的中间方程。（高考数学每一个中间步骤都有分数，得出几个步骤就可以拿满分）

CoT-SC

CoT-sc是对传统CoT方法的改进。由于相同的问题通常有不同的思维过程，CoT-sc通过探索更多的思维链来更准确地捕捉这种多样性。这样可以使输出决策更加忠实于问题的多个解决方法。

COT-SC: 通常来说，一个数学证明有不同的解法，找出最佳的解法就是cot-sc做的事情。出现最多的yi。
CoT-sc的一个局限是它并没有在每个思维链中进行对不同思维步骤的局部探索。这可能导致没有充分地探索所有的潜在思路。另外，使用“最频繁”的启发式只适用于输出空间有限的情况，比如多项选择问答，对于输出空间无限或者较大的问题，这种方法可能不够有效。

算法流程：

ToT作为LLM的一般问题解决方法有几个好处:

1. 通用性。IO、CoT、CoT- sc和自细化可以看作是ToT的特殊情况(即深度和宽度有限的树).
2. 模块化。基本LM以及思想分解、生成、评估和搜索过程都可以独立变化。
3. 适应性。可以容纳不同的问题属性、LM功能和资源约束。
4. 方便。不需要额外的训练，只需要一个预训练的LM就足够了。

• 如何将中间过程分解为思想步骤

根据不同的问题，一个想法可以是几个单词(填字游戏)，一行方程(24点游戏)，或一整段写作计划(创意写作)。
一般来说，一个想法应该足够"小"，以便LMs可以生成有希望的和多样化的样本(例如，生成整本书通常太"大"而不连贯)，但又足够"大"，以便LMs可以评估其解决问题的前景(例如，生成一个令牌通常太"小"而无法评估)。

• 如何从每个状态生成潜在思想

1. CoT提示：当思想空间丰富(例如每个思想是一个段落，创意写作)时，这种方法效果更好。
2. 使用“建议提示”顺序提出想法：这在思维空间受限时效果更好(例如，每个思维只是一个单词或一行，24点和填词游戏)，因此在相同的上下文中提出不同的思维可以避免重复

• 如何启发式地评估状态

通过使用LM对状态进行推理。当适用时，这种深思熟虑的启发式比编程规则更灵活，比学习模型更有效。与思想生成器类似，我们考虑两种策略来单独或一起评估状态:

1. 独立地为每个状态赋值:以产生一个标量值(例如1-10)或一个分类(例如sure/likely/impossible)，它可以被启发地转化为一个值。这种评价性推理的基础可能因问题和思维步骤而异。在这项工作中，我们通过一些前瞻性模拟来探索评估(例如，快速确认5,5,14可以通过5 + 5 + 14达到24，以及常识(例如，1 2 3太小而无法达到24。
2. LLM投票
   当问题的成功难以直接评价时(例如，段落的连贯性)，比较不同的部分解决方案并投票选出最有希望的解决方案是很自然的。

• 使用哪种搜索算法

1. 广度优先搜索(BFS)(算法1)每一步维护一个由b个最有希望的状态组成的集合。这用于Game of 24和Creative Writing，其中树深度是有限的(T≤3)，并且可以评估初始思维步骤并将其修剪为一个小集合(b≤5)。
2. 深度优先搜索(DFS)(算法2)首先探索最有希望的状态，直到达到最终输出(t > T)，或者状态评估器认为不可能解决问题。在这两种情况下，dfs都回溯到父状态以继续探索。

主要实验对象：

24点游戏

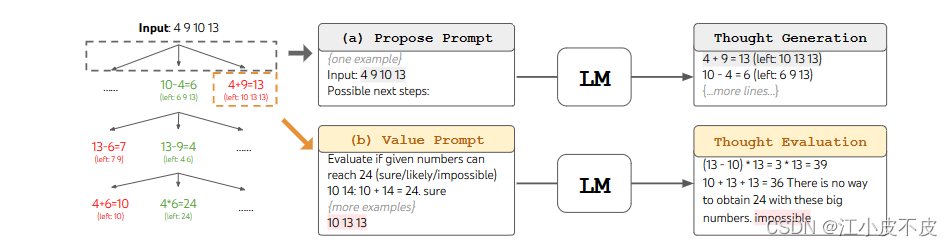
游戏24点是一个数学推理挑战，其目标是使用4个数字和基本的算术运算(±**/)来获得24。例如，给定输入“4 9 10 13”，解输出可能是“(10 - 4)*(13 - 9)= 24”。

1. 思维生成器

对于思维链(CoT)提示，用3个中间方程增加每个输入-输出对，每个方程操作两个剩余的数字。

例如，输入“4 9 10 13”，想法可能是：

4 + 9 = 13（剩余10 13 13）

10 - 4 = 6 （剩余6 9 13）

2. 思维验证器

   验证上一步生成的数字能不能到达24点。

   我们在ToT中执行广度优先搜索(BFS)，在每一步中我们保留最好的b = 5个候选者。为了在ToT中执行深思熟虑的BFS，如图2(b)所示，我们提示LM评估每个思想候选人在达到24方面的确定/可能/不可能

   其目的是促进可以在几次前瞻性试验中确定的正确的部分解决方案，并基于“太大/太小”的常识消除不可能的部分解决方案，并保留其余的“可能”。

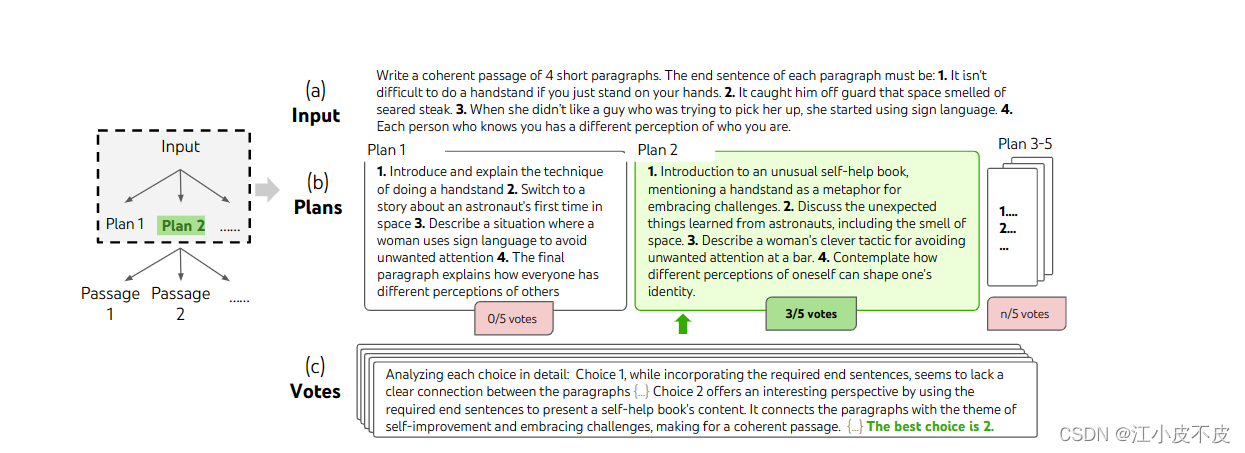
创意写作

在一个随机选择的创意写作任务中深思熟虑的搜索步骤。给定输入，LM对5个不同的计划进行抽样，然后投票5次以决定哪个计划是最好的。因此，多数选择用于使用相同的抽样投票过程编写输出通道。

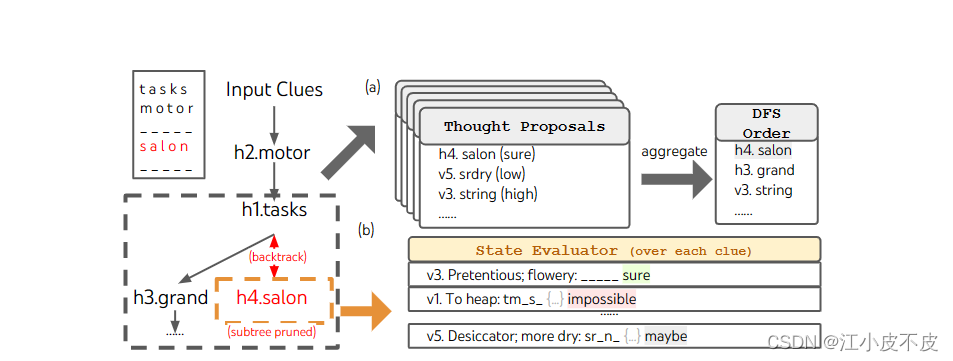
填字游戏

目标不仅仅是解决任务，因为更一般的填字游戏可以很容易地通过专门的NLP任务，利用大规模检索而不是LLM。相反，我们的目标是探索LM作为一般问题解决器的极限。利用深度优先搜索(算法2)，不断探索最有希望的后续单词线索，直到状态不再有希望，然后返回到父状态以探索其他想法。为了使搜索易于处理，后续的想法被限制不改变任何填充的单词或字母，因此ToT最多有10个中间步骤。

存在的问题：

然而，使用代表思想的 PAL 公式作为代码，这使得很难解决我们在本文中考虑的创造性写作等具有挑战性的任务。因此，我们的 Tree-of-Thought 公式更通用的任务，并处理 GPT-4 仅使用标准提示实现了非常低的准确度的具有挑战性的任务。

总结：

此外，ToT 等搜索方法比采样方法需要更多的资源（例如 GPT-4 API 成本），以提高任务性能，但 ToT 的模块化灵活性允许用户自定义此类性能成本权衡，并且正在进行的开源努力 在不久的将来应该很容易降低此类成本。最后，这项工作的重点是使用现成的 LM，并使用 ToT 风格的高级反事实决策（例如，考虑下一段的潜在选择，而不是预测下一个标记）微调 LM 可能会有机会增强 LM 的问题解决能力。

更广泛的影响。ToT是一个框架，它使LMs能够更自主、更智能地做出决策和解决问题。虽然目前的任务仅限于推理和搜索问题，但涉及与外部环境或人类交互的未来应用可能带来潜在的危险，例如促进LMs的有害使用。另一方面，ToT还提高了模型决策的可解释性和人为对齐的机会，因为结果表示是可读的高级语言推理，而不是隐式的低级令牌值。

思想树框架提供了一种方法，将解决问题的经典见解转化为当代lm的可操作方法。同时，LMs解决了这些经典方法的一个弱点，提供了一种方法来解决不容易形式化的复杂问题，比如创造性写作。我们认为LMs与经典人工智能方法的交叉是未来工作的一个令人兴奋的方向。