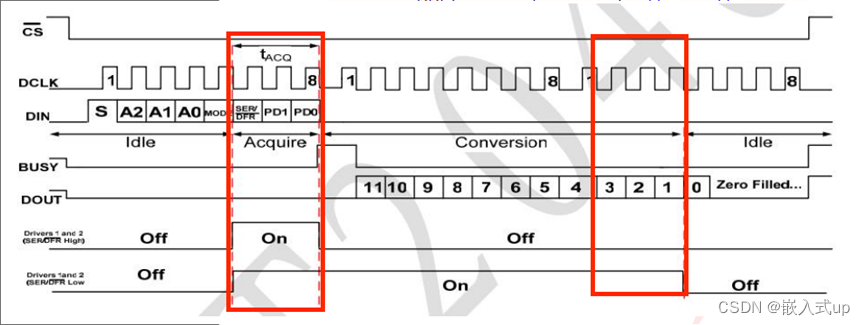
论文链接:https://www.nature.com/articles/s41467-022-30706-9
一、为什么要研究高阶网络?
复杂网络跟我们生活息息相关,例如社交网络的信息传播,疾病的感染扩散和基因调控网络的相互作用等。越来越多的研究突破了传统网络中两个节点之间成对的关系,研究三个,四个甚至更多节点之间的高阶关系。例如,科学家合作发表论文,成对的连接只能描述两个作者的合作,却无法表示多个作者的情况。这些高阶关系在社会、信息和生物的网络中是客观存在且重要的,但是我们很难直接获取这样的高阶结构,往往依靠观测数据来重建复杂网络中的高阶关系。
二、文章动机:
现有方法是从简单网络或是成对节点的观测中重建出网络中的高阶关系。时间序列作为复杂系统中的原始观测数据,是网络重建任务中不可忽略的。同时,直接从时间序列中重建高阶网络,是对复杂系统的推理建模,是具有挑战的任务。
今天介绍的这篇文章从二元时间序列中重构单纯复形(高阶网络结构),是具有代表性和开创性的工作。
关键词: 高阶网络,网络重构,时间序列,单纯复形
三、什么是单纯复形(Simplices)?


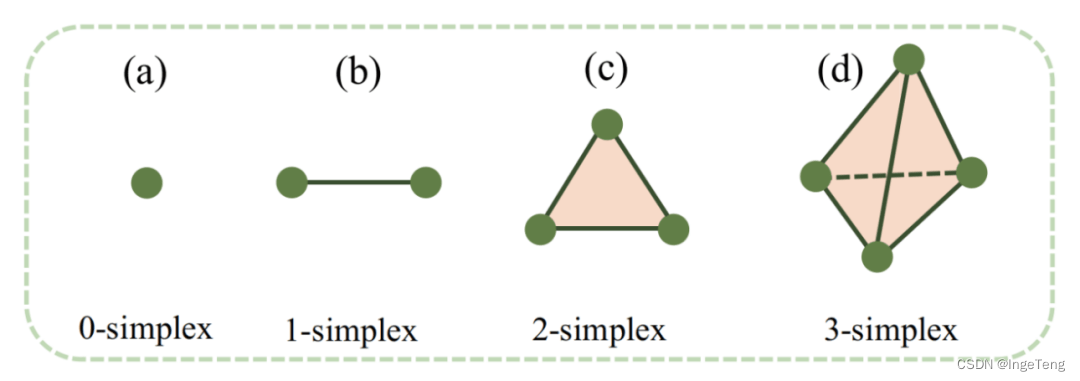
单纯复形是高阶网络的一种形式,它是由一系列单纯形组成的集合,有强大的数学形式做支撑,例如上图1(a) 为普通的网络连接,图1(b) 中黑色的边可以看做1-simplices,黄色的完整三角形可以看做2-simplices。在作者合作网络中,任意两个作者合作的关系,可以看做1-simplices,三个作者一起合作的关系组成2-simplices。当然,四人或是多人合作的关系为3-simplices或n-simplices,如下图所示。单纯复形突破了简单两两成对之间的关系,形成了高阶网络。
四、算法方法
本文从重构2-simplices网络出发,利用社会传染病传播模型和本文提出的Simplicial Ising动态模型生成考虑高阶信息的二元时间序列数据。
算法重构可以分为三个部分:
-
基于动力学模型生成的时序数据建立似然函数;
-
利用统计学方法(EM)重构网络连接概率;
-
2-step重构策略,优化提高框架效率。
算法框架细节如下:
1、建立似然函数
根据动力学生成的时序建立条件概率模型,个体 i 由其它单个个体 j 传染或激发的概率为:



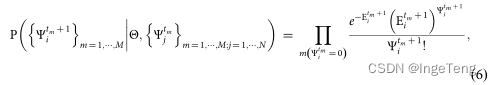
2、EM重构
建立基于最大似然估计的EM算法:
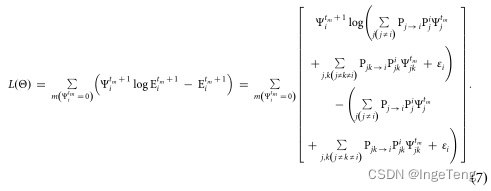


3、2-step策略
首先预测每一个个体(节点)的近似邻居,并提取预测邻居的时序,然后基于该数据重建出每个个体(节点)的两体和三体连接。该策略旨在保证精度的同时,减少计算时间。具体如图3所示

图3(a) 是基于2-simplices的高级动力学的网络,生成图b中的时间序列数据。根据上述介绍的算法,其中a->b->c->d->e 基于上述算法框架 1和 2,直接通过统计学方式计算每个连接的最大概率;a->b->f->h->h>i 为加入3 中的2-step策略的整体算法框架。
实验结果
为了验证算法框架的重建性能,本文基于两种高阶动力学数据(社会传染病传播和单纯形Ising动态),对3种人工合成的2-simplices(ERSC, SFSC, SWSC)和4个真实2-simplices(Hypertext2009, Thiers12, InVS15, LyonSchool)网络进行重建。

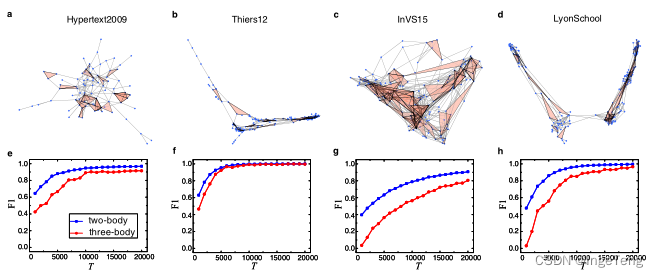
讨论
从实验可以看出该框架在合成2-simplices和真实2-simplices的鲁棒性和重建精度都很高,但是仍然存在一些限制。例如本文从二进制的时间序列中重建高阶网络,如何从实数或更一般的真实情形(数据缺失,噪声)重建高阶网络。并且本文对于时序的长度要求是较高的,如何从更短的时序中重建单纯复形或超图,都是后续有待研究的课题。