目录
- 1. numpy的介绍
- 2. numpy库产生矩阵
- 2.1 numpy将列表转换成矩阵
- 2.2 numpy创建矩阵
- 3. numpy的基础运算
- 4. numpy的基础运算2
- 5. 索引
1. numpy的介绍
numpy库是numpy是python中基于数组对象的科学计算库。
2. numpy库产生矩阵
2.1 numpy将列表转换成矩阵
import numpy as np
array = np.array([[1, 2, 3],
[4, 5, 7]]) # 将列表转换成矩阵
print(array) # 输出矩阵
print('number of dim', array.ndim) # 输出矩阵的维度
print('shape', array.shape) # 输出矩阵的形状
print('size', array.size) # 输出矩阵的大小
在这段代码中,首先导入numpy库,然后使用array()方法将列表转换成矩阵。

2.2 numpy创建矩阵
- 使用array()方法产生一维和二维矩阵
import numpy as np
# 一维矩阵
a = np.array([2, 3, 4], dtype=np.int64)
print(a, a.dtype)
# 二维矩阵
a = np.array([[1, 2, 3],
[4, 5, 6]])
print(a)

- 使用zeros()方法产生全0矩阵
# 0矩阵
a = np.zeros((3, 4))
print(a)

- 使用ones()方法产生全1矩阵
# 1矩阵
a = np.ones((3, 4))
print(a)

- 使用arrange()方法产生均匀矩阵、
# 均匀矩阵
a = np.arange(10, 20, 2) # 10-20,步长为2
print(a)
a = np.arange(12).reshape((3, 4)) # 将形状改变成3*4
print(a)

- 使用linspace()方法产生一维行向量
# 一维行向量
a = np.linspace(1, 10, 6)
print(a)
a = np.linspace(1, 10, 6).reshape((2, 3))
print(a)
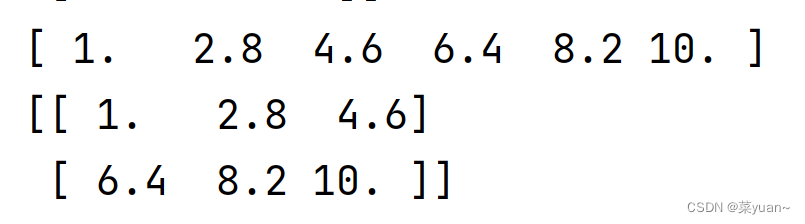
- 完整代码
import numpy as np
# 一维矩阵
a = np.array([2, 3, 4], dtype=np.int64)
print(a, a.dtype)
# 二维矩阵
a = np.array([[1, 2, 3],
[4, 5, 6]])
print(a)
# 0矩阵
a = np.zeros((3, 4))
print(a)
# 1矩阵
a = np.ones((3, 4))
print(a)
# 均匀矩阵
a = np.arange(10, 20, 2) # 10-20,步长为2
print(a)
a = np.arange(12).reshape((3, 4)) # 将形状改变成3*4
print(a)
# 一维行向量
a = np.linspace(1, 10, 6)
print(a)
a = np.linspace(1, 10, 6).reshape((2, 3))
print(a)
3. numpy的基础运算
- 加法运算
import numpy as np
a = np.array([10, 20, 30, 40])
b = np.arange(4)
print(b)
# 加法
c = a + b
print(c)
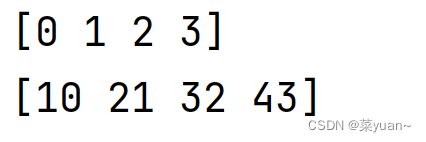
- 减法运算
# 减法
c = a - b
print(c)
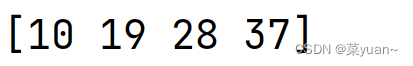
- 乘方运算
# 乘方
b = b ** 2
print(b)
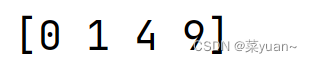
- 正弦运算
# 正弦
c = 10 * np.sin(a)
print(c)
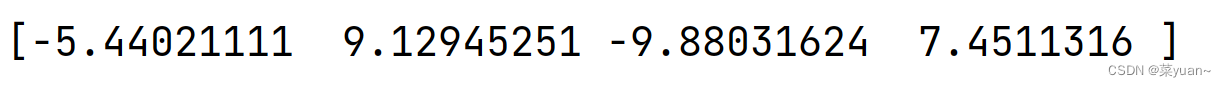
- 矩阵相乘,使用*是矩阵点乘,使用dot()方法是矩阵乘法
a = np.array([[10, 20],
[30, 40]])
b = np.arange(4).reshape((2, 2))
print(a)
print(b)
c = a * b # 矩阵对应相乘,点乘
c_dot = np.dot(a, b) # 矩阵相乘
c_dot_2 = a.dot(b)
print(c)
print(c_dot)
print(c_dot_2)

- 求和运算,最大值和最小值
# 随机矩阵
a = np.random.random((2, 4))
print(a)
print(np.sum(a))
print(np.max(a))
print(np.min(a))
print(np.sum(a, axis=1)) # 对每一行求和
print(np.sum(a, axis=0)) # 对每一列求和

- 完整代码
import numpy as np
a = np.array([10, 20, 30, 40])
b = np.arange(4)
print(b)
# 加法
c = a + b
print(c)
# 减法
c = a - b
print(c)
# 乘方
b = b ** 2
print(b)
# 正弦
c = 10 * np.sin(a)
print(c)
# 矩阵相乘
a = np.array([[10, 20],
[30, 40]])
b = np.arange(4).reshape((2, 2))
print(a)
print(b)
c = a * b # 矩阵对应相乘,点乘
c_dot = np.dot(a, b) # 矩阵相乘
c_dot_2 = a.dot(b)
print(c)
print(c_dot)
print(c_dot_2)
# 随机矩阵
a = np.random.random((2, 4))
print(a)
print(np.sum(a))
print(np.max(a))
print(np.min(a))
print(np.sum(a, axis=1)) # 对每一行求和
print(np.sum(a, axis=0)) # 对每一列求和
4. numpy的基础运算2
import numpy as np
A = np.arange(2, 14).reshape((3, 4))
print(A)
print(np.nanargmin(A)) # 对最小值的索引
print(np.nanargmax(A)) # 对最大值的索引
print(np.mean(A)) # 平均值
print(np.median(A)) # 中位数
print(np.cumsum(A)) # 累加和
print(np.diff(A)) # 累差
print(np.nonzero(A)) # 输出非零的数的位置
print(np.sort(A)) # 逐行进行排序
print(np.transpose(A)) # 矩阵转置
print(A.T) # 矩阵转置
print((A.T).dot(A)) # 实对称矩阵
print(np.clip(A, 5, 9)) # A中小于5的数等于5,大于9的数等于9,其余不变
print(np.nanmean(A, axis=0)) # 对列进行计算平均数
print(np.nanmean(A, axis=1)) # 对行进行计算平均数
结果:
[[ 2 3 4 5]
[ 6 7 8 9]
[10 11 12 13]]
0
11
7.5
7.5
[ 2 5 9 14 20 27 35 44 54 65 77 90]
[[1 1 1]
[1 1 1]
[1 1 1]]
(array([0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2], dtype=int64), array([0, 1, 2, 3, 0, 1, 2, 3, 0, 1, 2, 3], dtype=int64))
[[ 2 3 4 5]
[ 6 7 8 9]
[10 11 12 13]]
[[ 2 6 10]
[ 3 7 11]
[ 4 8 12]
[ 5 9 13]]
[[ 2 6 10]
[ 3 7 11]
[ 4 8 12]
[ 5 9 13]]
[[140 158 176 194]
[158 179 200 221]
[176 200 224 248]
[194 221 248 275]]
[[5 5 5 5]
[6 7 8 9]
[9 9 9 9]]
[6. 7. 8. 9.]
[ 3.5 7.5 11.5]
5. 索引
import numpy as np
# 一维数组
A = np.arange(3, 15)
print(A)
print(A[3]) # 对A中的值进行索引,位置是3
# 二维矩阵
A = np.arange(3, 15).reshape((3, 4))
print(A)
print(A[1]) # 对A中的值进行索引,位置是1,为第一行的数
print(A[1][1]) # 对A中第一行第一列的数进行索引
print(A[1, 1]) # 对A中第一行第一列的数进行索引
print(A[1, :]) # A中第一行的所有的数
print(A[:, 1]) # A中第一列的所有的数
print(A[1, 1:3]) # A中第一行的1-3的数,取左不取右
# 输出矩阵中每一行的数
for row in A:
print(row)
# 输出矩阵中每一列的数
for col in A.T:
print(col)
# 输出A中每一个数
print(A.flatten()) # 将矩阵转换成一维数组
for item in A.flat:
print(item)
结果:
[ 3 4 5 6 7 8 9 10 11 12 13 14]
6
[[ 3 4 5 6]
[ 7 8 9 10]
[11 12 13 14]]
[ 7 8 9 10]
8
8
[ 7 8 9 10]
[ 4 8 12]
[8 9]
[3 4 5 6]
[ 7 8 9 10]
[11 12 13 14]
[ 3 7 11]
[ 4 8 12]
[ 5 9 13]
[ 6 10 14]
[ 3 4 5 6 7 8 9 10 11 12 13 14]
3
4
5
6
7
8
9
10
11
12
13
14