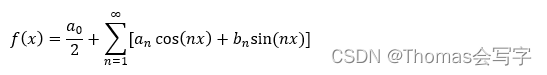10.1 无监督学习的定义

监督学习：我们有一些列标签，然后用假设函数去拟合它

无监督学习：给出的数据不带任何标签。对于无监督学习来说，需要做的就是将数据输入到算法中，让算法找到一些隐含在数据中的结构，通过图中的这些数据，能通过算法找到一个结果就是这个数据集中的点可以分成两组分开的点集（簇）。这种能分出来的簇的算法被称为聚类算法。

 10.2 K-means算法（K均值）

在聚类问题中，会给定一组未加标签的数据集，会希望有一个算法能够自动地将这些数据分成有紧密关系的子集或是簇。K-means算法是比较热门的最为广泛运用的聚类算法。

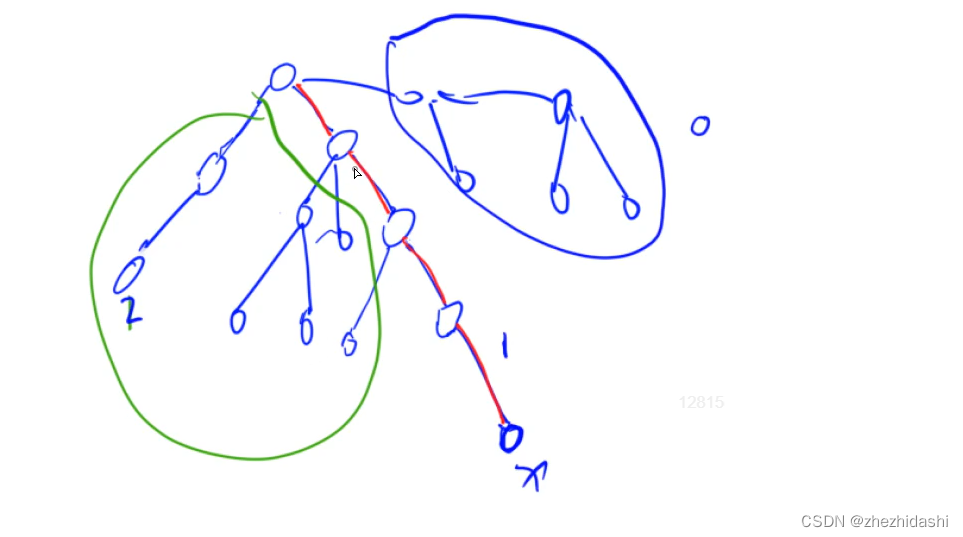
对于没有标签的数据来说，第一步随机生成两点（下图的红蓝两个×），也叫做聚类中心。随机两点是因为想把下图的数据聚类成两类（首先根据划分聚类的个数，随机设置聚类中心的位置）。然后遍历所有的数据，把每个数据分配到离它最近的坐标，对于同一个簇的数据计算它们坐标的中心位置，并设置为新的聚类中心，以此不断的迭代。

 K-means算法接受两个输入，一个是参数K，表示想从数据中聚类出的簇的个数；另一个就是一系列无标签的只用x来表示的数据集，并且约定是一个n维实数向量。

K-means算法步骤：

1. 随机初始化K个聚类中心，记作
2. K-means的内循环，簇分配步骤：对每个训练样本，使用变量来表示第1到第K个最接近的聚类中心；移动聚类中心：对于每个聚类中心，也就是对于k=[1,K]，就表示这个簇中所有点的均值。

假设有，对应得，表示都被分配给了聚类中心2，这个时候要算，就是把相加除以4。得到的结果就是聚类中心2移动的结果。

 如果存在一个没有点的聚类中心，最常见的做法就是直接移除那个聚类中心，但如果这样做得到的簇的总数为K-1而不是K。有时你的确需要K个簇时，这时可以重新随机初始化这个聚类中心得到K个簇并且每个点都有聚类中心。

K-means的常见应用：它可以用来解决分离不佳的簇的问题，具体情况如下：

10.2.1 K-means的初始化

初始化K-means聚类算法可以引导我们讨论如何使算法避开局部最优。

随机初始化聚类中心：当聚类数量很少时，如果初始化的位置不够好，会得到一个局部最优解，解决方案是多次随机初始化，从而得到一个全局最优解。

通常用来初始化K-means聚类的方法是：随机挑选K个训练样本，设定，让它们等于这个K个样本。

10.2.2 聚类数量的选择

如何选择聚类数量或者说如何选择参数K的值？

当谈论到选择聚类数量的方法时，会谈到一个方法叫做“肘部法则”

肘部法则：所要做的改变K也就是聚类总数。先用一个类来聚类这意味着所有的数据都会分到一个类里，然后计算代价函数即畸形函数J。然后再用两个类来跑K-means聚类，可能多次随机初始化也可能随机初始化一次。

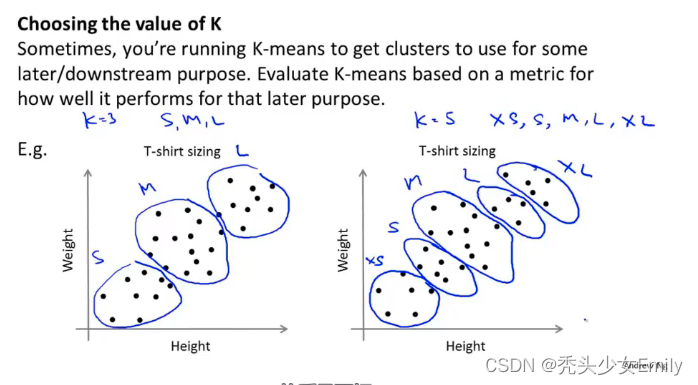
 得到聚类数量和代价的图像，根据肘部原则选取（一般不用）；或者根据k均值聚类的目的来做判断，比如做衣服尺寸的聚类分析，根据市场需求，3个聚类or5个聚类更适合市场营销等等。