目录
运动的描述
期末考点
质点运动学
牛顿运动定律知识点
题1(牛顿第二定律)
题目描述
题解
题2 (圆周运动)
题目描述
题解
运动的描述
期末考点
1.速度和加速度的推导
平均速度平均速度反映的只是在一段时间内位移的变化,如果需要精准的地知道质点在某一时刻t(或某一位置)的运动情况,应使
尽量减小而趋近于零,用平均速度的极限值——瞬时速度来描述。
瞬时速度(速度):


从速度矢量图可以看出,在时间内质点速度的增量为
与平均速度的定义类似,平均加速度为:
同理,引入瞬时加速度的概念,
质点在某时刻或某位置的瞬时加速度(简称加速度)等于当时间趋近于零时平均加速度的极限值,
2.匀变速直线运动公式推导
(1)把数学式改写成
已知其a为恒量,质点的初始条件为t=0,v=v0,两边同时积分,得
解得:
即第一个公式,
(2)把数学式根据(1)改写成
整理成
两边积分,得
解得:,即第二个公式
(3)把加速度改写成
于是,有:
两边积分,得
解得:
即第三个公式,
3.圆周运动-线量和角量的变换 总加速度
总加速度
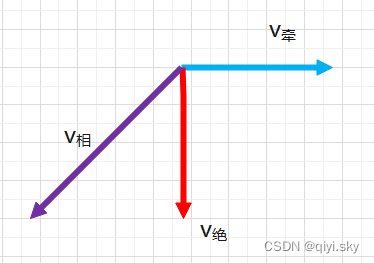
4.相对运动-绝对速度 相对速度 牵连速度成矢量三角形
质点运动学
牛顿运动定律知识点
1.牛顿第一定律
任何物体都要保持其静止或匀速直线运动状态,直到外力迫使它改变运动状态为止。
当时,
恒矢量
2.惯性参考系
惯性——物体保持其运动状态不变的特性。
如果物体在一参考系中不受其它物体作用,而保持静止或者匀速直线运动,这个参考系就称为惯性参考系。
3.牛顿第二定律
动量为的物体,在合外力
的作用下,其动量随时间的变化率应当等于作用于物体的合外力.
,当
时,m为常量.
故而可以写成:
4.牛顿定律的矢量性
5.牛顿第三定律
(物体间相互作用规律)
6.物理量的单位
| 物理量 | 长度L | 质量M | 时间T | 电流I | 热力学温度 | 物质的量 | 发光强度 |
|---|---|---|---|---|---|---|---|
| 单位名称 | 米 | 千克 | 秒 | 安培 | 开尔文 | 摩尔 | 坎德拉 |
| 符号 | m | kg | s | A | K | mol | cd |
7.量纲
导出量与基本量之间的关系式。基本量纲:L、M、T。
如:
速度的量纲是
角速度的量纲是
力的量纲是
题1(牛顿第二定律)
题目描述
质量为m的子弹以速率竖直射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为K,忽略子弹的重力。求:(1)子弹射入沙土后,速度随时间变化的函数式;(2)子弹进入沙土的最大深度。
题解
第一问,求速度随时间变化的函数式,我们先受力分析
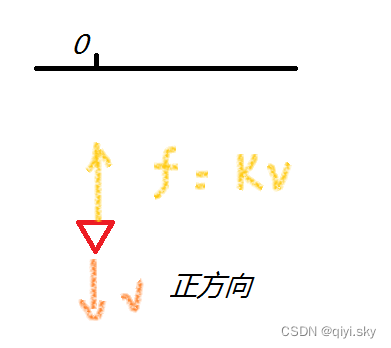
受到摩擦力的作用,我们定竖直向下为正方向。
由牛顿第二定律得,
变换加速度,有:
分离变量,整理,并两边同时积分:
解得:,最后整理一下就可以得到速度随时间变化的函数式了:
第二问,求子弹进入沙土的最大深度,可以利用前面的关系式得到速率与深度的关系。
由第一问知,
变换一下,,没有影响原式的结果吧,而这里的
就是v。
所以有,.
同样分离变量,两边同时积分:,初速度为v0,射入沙土后减为0.
解得:
题2 (圆周运动)
题目描述
质量为m的质点沿半径为R的圆周按规律,其中
是路程,
是时间,
均为常量。求t时刻作用于质点的切向力和法向力?
题解
由牛二可简单地得出:
接下来就分别求出加速度,
切向:
所以t时刻作用于质点的切向力为:
法向:
所以t时刻作用于质点的法向力为:
end