【数据结构】--单链表力扣面试题⑦环形链表

news2024/11/19 13:37:52

注：本篇文章不含环形链表的数学推理证明，只提供图解等思路

环形链表是一个非常经典的问题

题述：给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续追踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从0开始）。如果pos是-1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true。否则，返回 false。

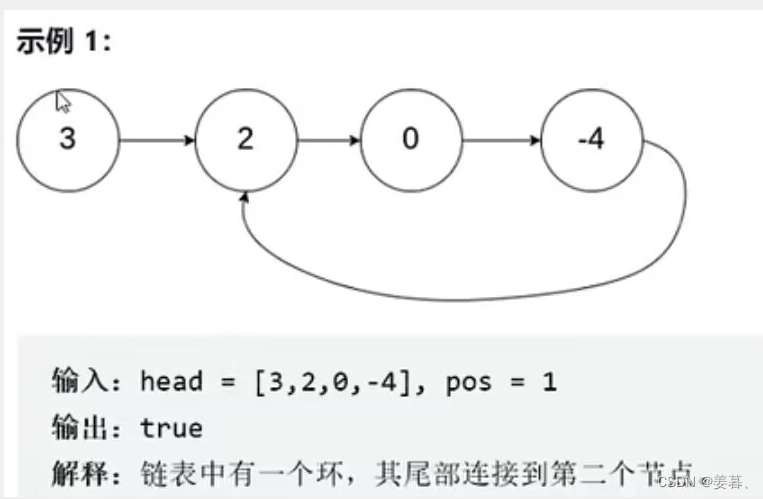
进阶：

你能用o(1)（即，常量）内存解决此问题吗？

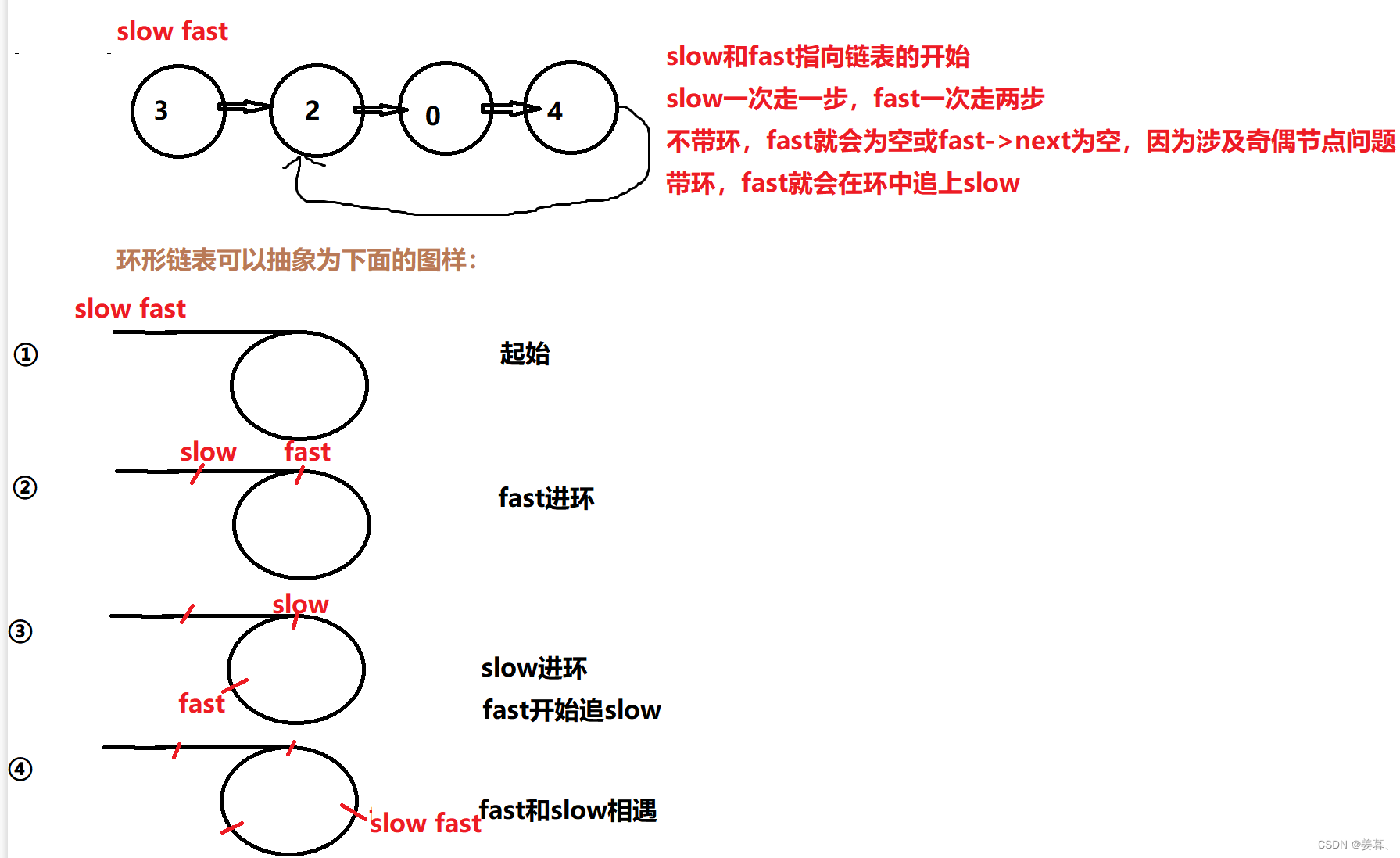
思路：本题难在分析，代码却很简单。那么链表带环的问题不能用正常的方式去遍历，因为会死循环。正确的思路是利用快慢指针

以下都是经典的环形链表

下面为图解思路：

以下是利用环形链表的结论得出，可以直接拿来用，难的在于如果推得环形链表的这个结论的

#include<Stdio.h>
#include<stdbool.h>
#include<stdlib.h>

struct ListNode
{
	int val;
	struct ListNode* next;
};
bool hasCycle(struct ListNode* head)
{
	struct ListNode* slow = head, * fast = head;
	while (fast && fast->next)//因为对于快指针奇偶节点的结束条件不同
	{
		slow = slow->next;
		fast = fast->next->next;
		if (slow = fast)
		{//如果是环一定能走到相等
			return true;
		}
	}
	return false;
}
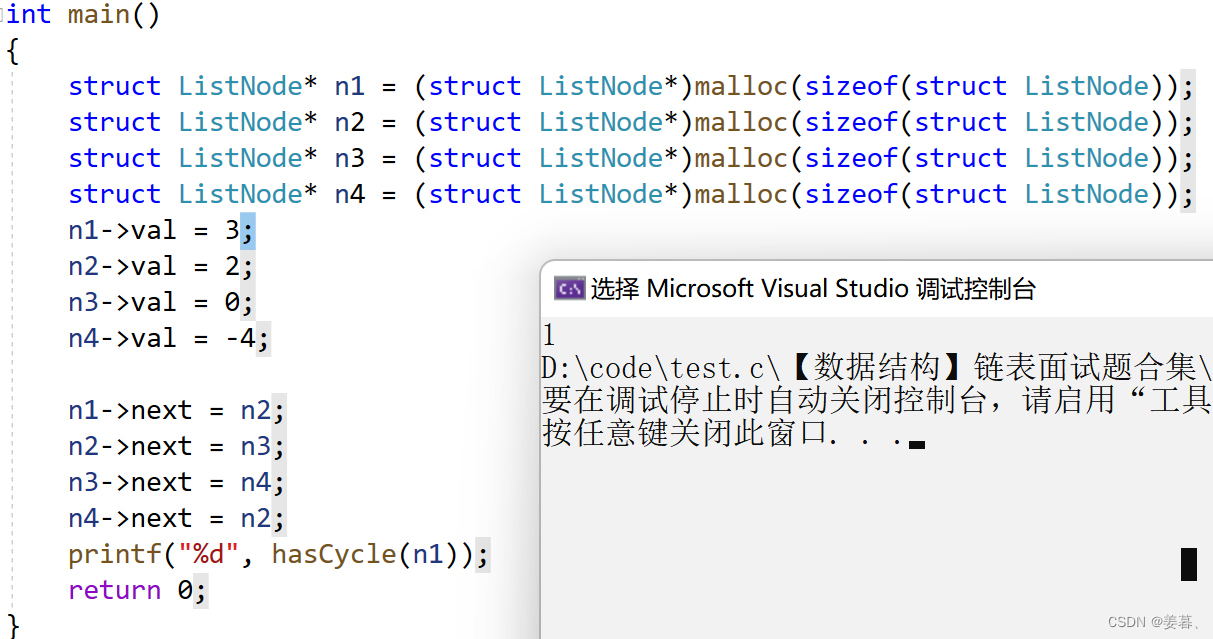
int main()
{
	struct ListNode* n1 = (struct ListNode*)malloc(sizeof(struct ListNode));
	struct ListNode* n2 = (struct ListNode*)malloc(sizeof(struct ListNode));
	struct ListNode* n3 = (struct ListNode*)malloc(sizeof(struct ListNode));
	struct ListNode* n4 = (struct ListNode*)malloc(sizeof(struct ListNode));
	n1->val = 3;
	n2->val = 2;
	n3->val = 0;
	n4->val = -4;

	n1->next = n2;
	n2->next = n3;
	n3->next = n4;
	n4->next = n2;
	printf("%d", hasCycle(n1));
	return 0;
}