💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
文献来源:
随着环境污染和能源短缺问题日益严重,以新能源发电技术为基础的分布式电源( DG) 越来越广 泛地应用于配电网中。但由于新能源发电的随机性、间歇性和高渗透率,分布式电源的接入增加了配电网潮流的波动程度,有必要重新考虑电压的调节方法,对引入分布式电源的配电网无功优化问题进行深入研究。
传统配电网的无功优化主要是通过调节变压器有载分接头以及投切无功补偿设备,在满足电能质 量要求的前提下实现网络损耗最小、系统能量损耗最小、平衡系统负荷、提高系统可靠性等目标。 当分布式电源接入配电网后,需要投入更多容量的无功补偿设备以增强调节电压的能力,这将增加不少成本。若能够考虑逆变器的无功特性,通过逆变器控制的分布式电源参与配电网的无功优化调节,则可大大减少配电网无功补偿设备的投资。
由于无功优化问题通常是非凸、非 线 性 且NP-难,它不像线性规划问题易于理解、找到全局最优解,其求解方法颇为复杂。目前国内外关于配电网无功优化的算法主要分为两类,一类是潮 流优化的经典算法,包括简化梯度法、牛顿法、支路交换法、内 点 法、线 性 规 划 法、二 次 规 划 法 等,这些方法应用广泛,但也存在编程困难、只能得到局部最优解等缺点。另一类是人工智能算法。
二阶锥规划( SOCP) 问题是在有限个二阶( 洛伦兹) 锥的笛卡尔乘积与仿射子空间的交集上求一
个线性目标函数的最小值或最大值,它实际上是半定规划的一种特例,是线性规划的推广,属于凸规划问题,可以在多项式时间内得到全局最优解,具有计算效率高,收敛速度快的优点。
二阶锥的标准形式为:

所建立的优化模型是一个非凸、非线性、NP-难的模型,难以直接得到最优解,因此需要对原模型进行松弛凸化处理。 首先采用相角松弛的方法,将复数变量转化为幅值形式的实数变量,从而将支路潮流方程线性化。
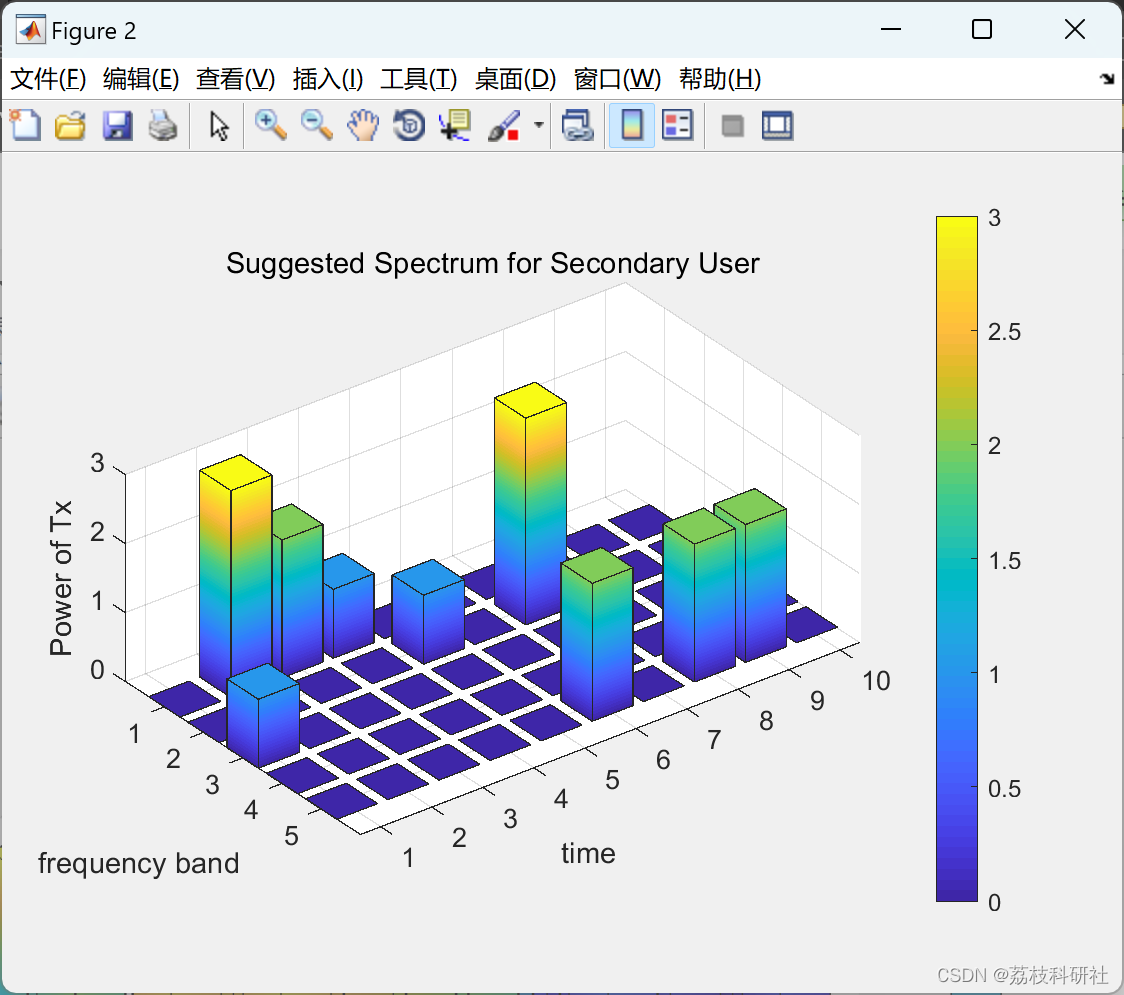
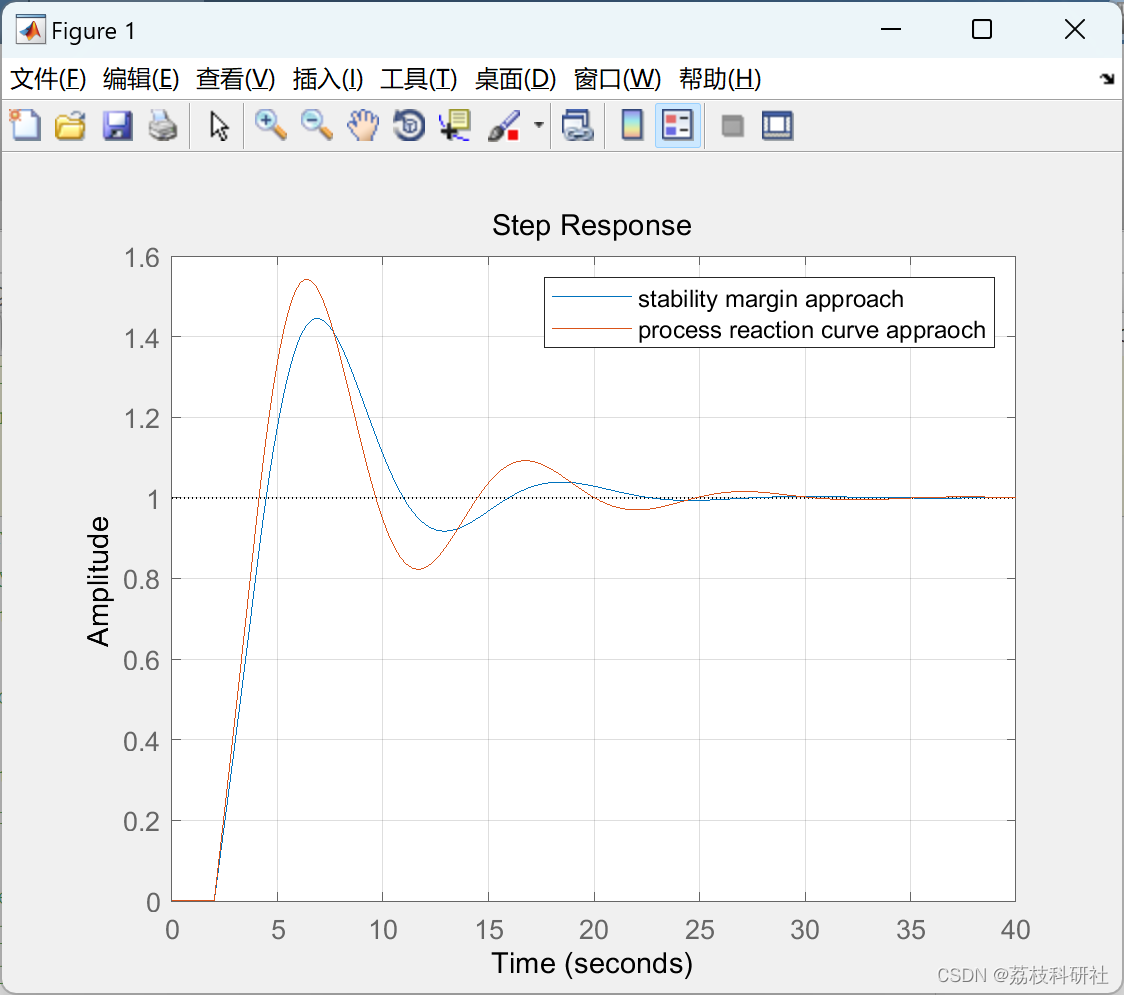
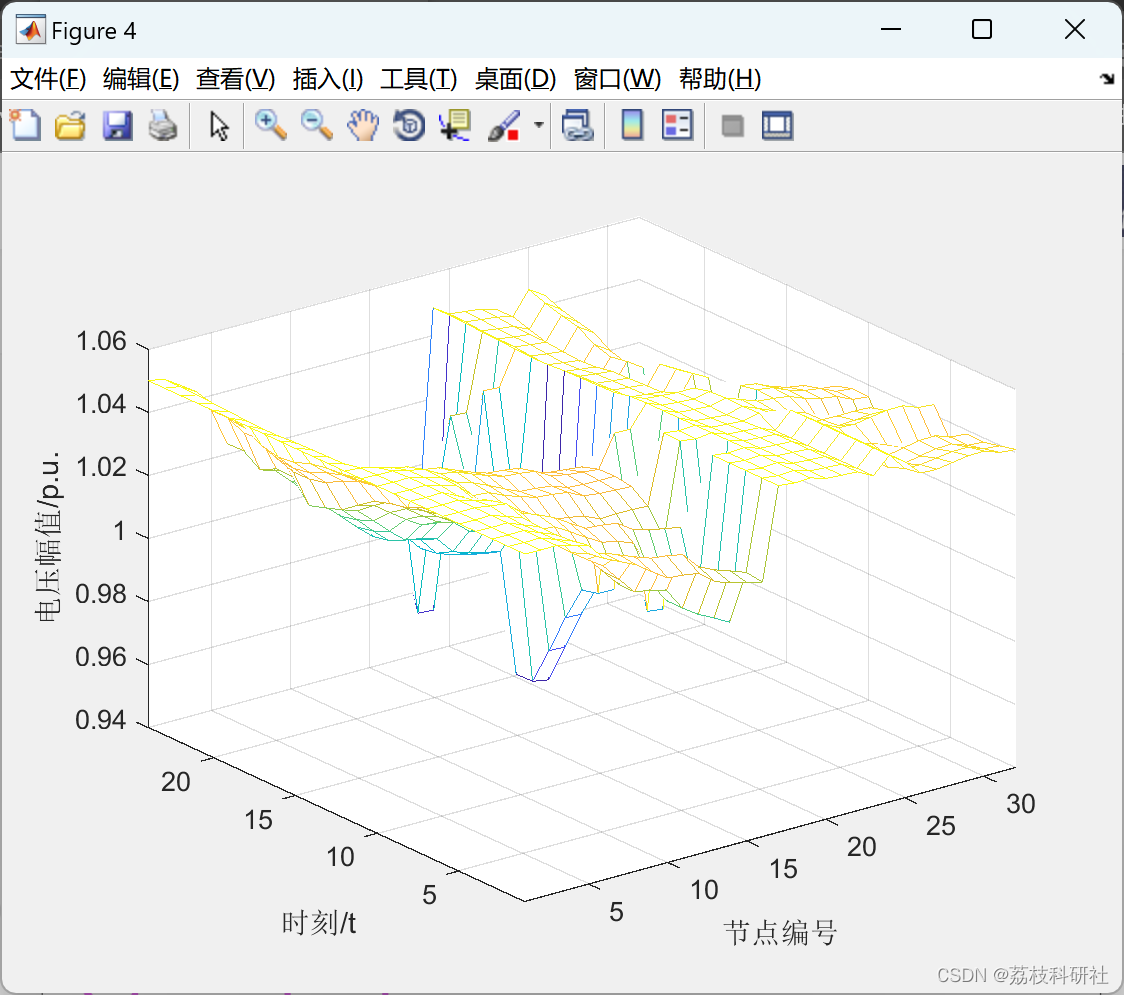
📚2 运行结果





🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]孙欣,严佳嘉,谢敬东等.“碳中和”目标下电气互联系统有功-无功协同优化模型[J].上海交通大学学报,2021,55(12):1554-1566.DOI:10.16183/j.cnki.jsjtu.2021.233.