【夜深人静算法介绍 | 第一篇】KMP算法

news2024/11/19 18:20:50

前言：

KMP算法简介：

引入概念：

前缀后缀

前缀表：

简单例子：

暴力遍历：

KMP算法：

KMP算法难点：

总结：

前言：

本篇我们将详细的从理论层面介绍一下什么是KMP算法，相对应的力扣刷题专栏里也会有相对应的习题，欢迎各位前往阅读。

KMP算法简介：

KMP算法是一种字符串匹配算法，用于在一个文本串中查找某个子串出现的位置。KMP算法的原理是根据模式串的特点，在匹配过程中避免重复匹配已经匹配过的部分。具体来说，KMP算法维护两个指针：i和j，表示当前匹配位置和模式串匹配的起点。当出现不匹配时，通过已匹配部分构建一个next数组，用以确定模式串下一次匹配起点的位置。

KMP算法的时间复杂度为O(n+m)，其中n为文本串长度，m为模式串长度。KMP算法应用广泛，例如在文件查找、模糊查询等领域都有广泛的应用。

KMP算法的本质就是跳过一部分暴力循环下的无效比较，达到节省时间复杂度的目的

引入概念：

前缀后缀

前缀：字符串中包含首字母但是不包含尾字符的所有子串

后缀：字符串中包含尾字母但是不包含首字符的所有子串

举例：

字符串aabaaf的前缀后缀分别有：

前缀	后缀
a	a
aa	aa
aab	baa
aaba	abaa
aabaa	abaaf

前缀表：

一个字符串中每一个子串都有自己的前缀和后缀，也就都有自己的最长相等前后缀长度，这些长度组成的一个数组，我们把它叫做前缀表

举例：
字符串aabaaf的前缀表：

子串	前缀	后缀	最长相等前后缀长度
a	无	无	0
aa	a	a	1
aab	a,aa	b,ab	0
aaba	a,aa,aab	a,ba,aba	1
aabaa	a,aa,aab,aaba	a,aa,baa,abaa	2
aabaaf	a,aa,aab,aaba,aabaa	f,af,aaf,baaf,abaaf	0

简单例子：

假设我们要在父串aabaabaaf中寻找子串aabaaf

暴力遍历：

正常情况是我们在父串中逐一遍历，父串与子串挨个匹配，直到找到与子串完全一致的为止：

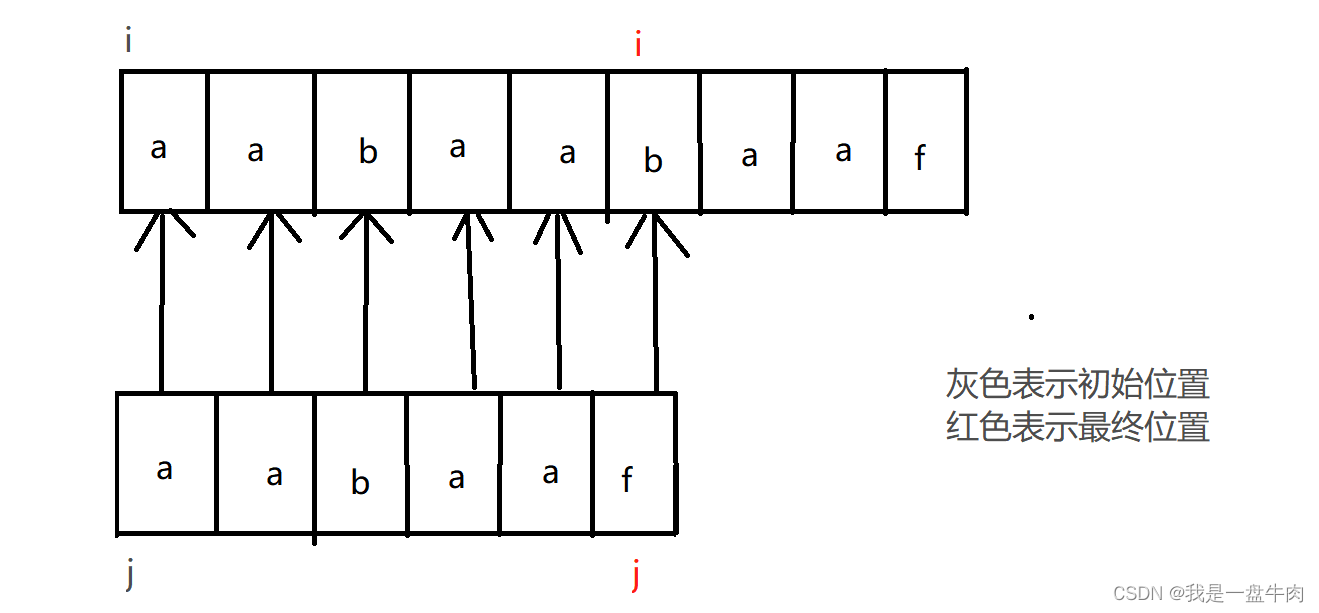
错误之后重新比较：

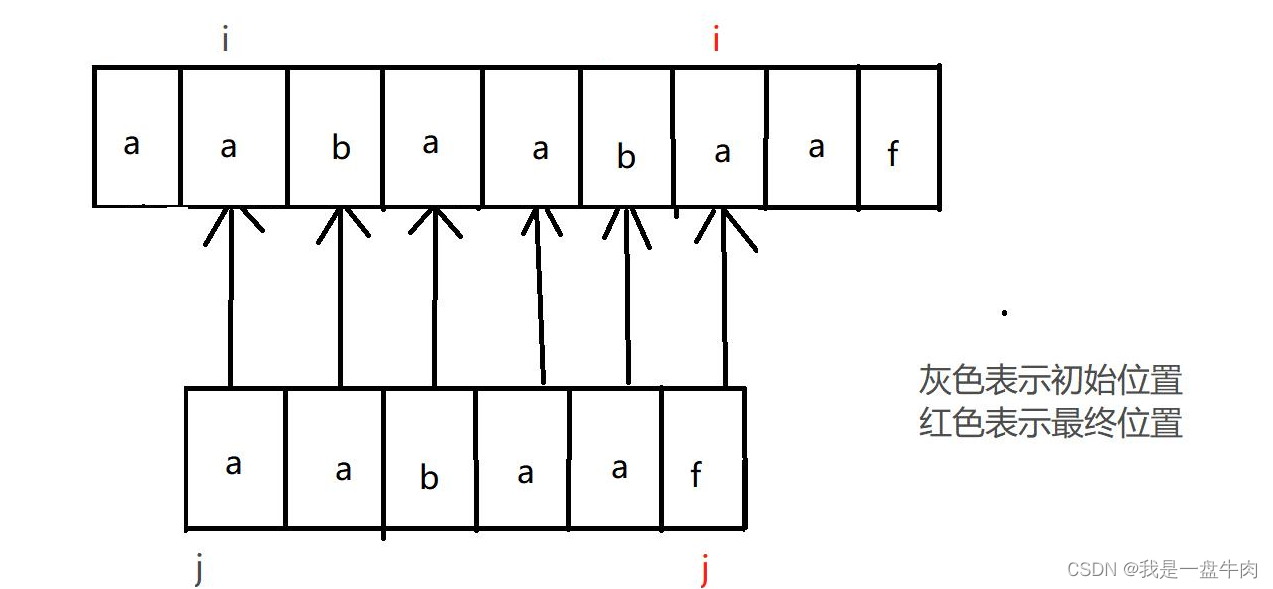
最终：

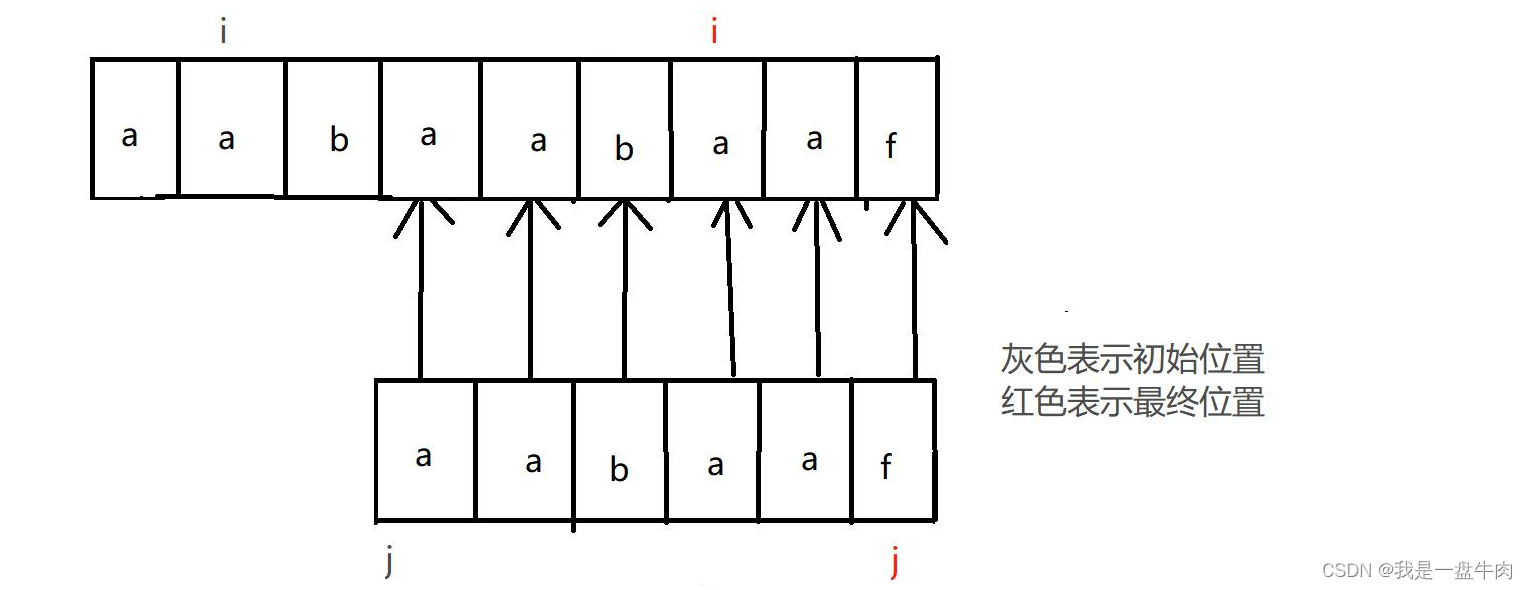
我们可以发现暴力遍历之所以时间复杂度高，是因为只要出错，父指针与子指针就会不断的回溯。第一次出错后，父类指针回溯到1，子类指针回溯到0，重新开始比较，第二次出错父类指针回溯到2，子类指针回溯到0，重新开始比较。如此类推。大量的回溯带来了高昂的时间成本，我们就在想如何才能够精简回溯，于是经过不懈努力，我们创造出了KPM算法。

KMP算法：

KMP算法采取了自定义i和j的回溯，通过控制i和j的回溯位置来降低回溯的时间成本。

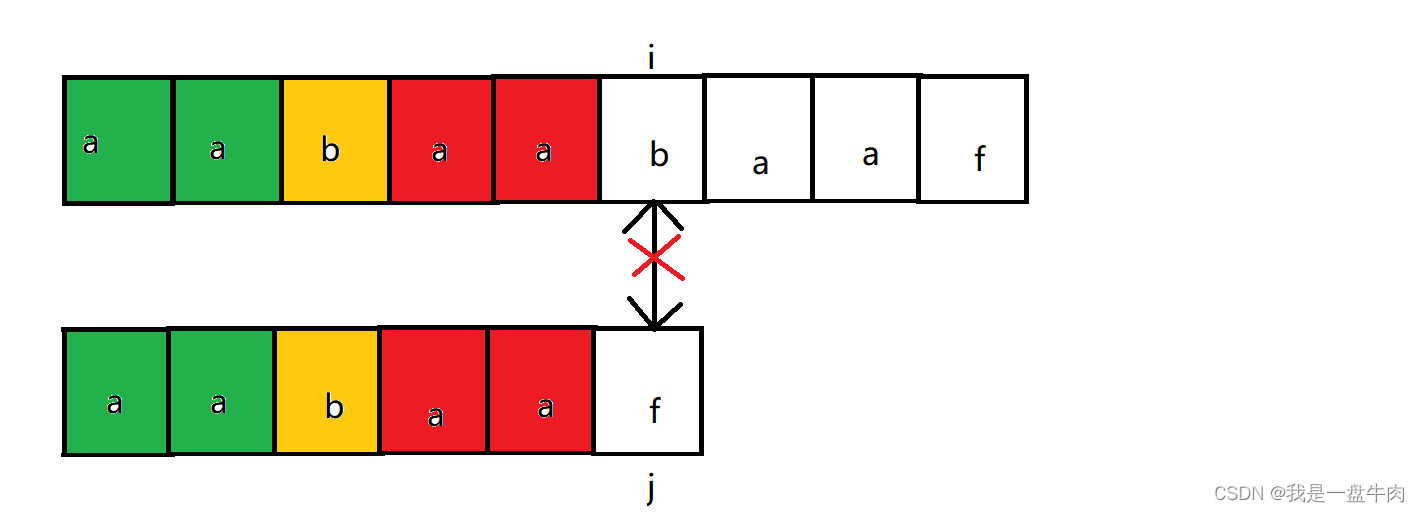
此时按照暴力遍历的思路，我们是让i等于1，j等于0重新开始第二轮遍历，但是我们KMP算法给出了新的思路：

我们不对已经比较过的字符串进行二次比较，就节省了回溯成本，既然绿色前缀和红色后缀相等，都是aa，那么下一次我们让子类的绿色前缀对齐父类的红色后缀，这样我们就不用回溯i和j，也可以开启新一轮的字符串对比

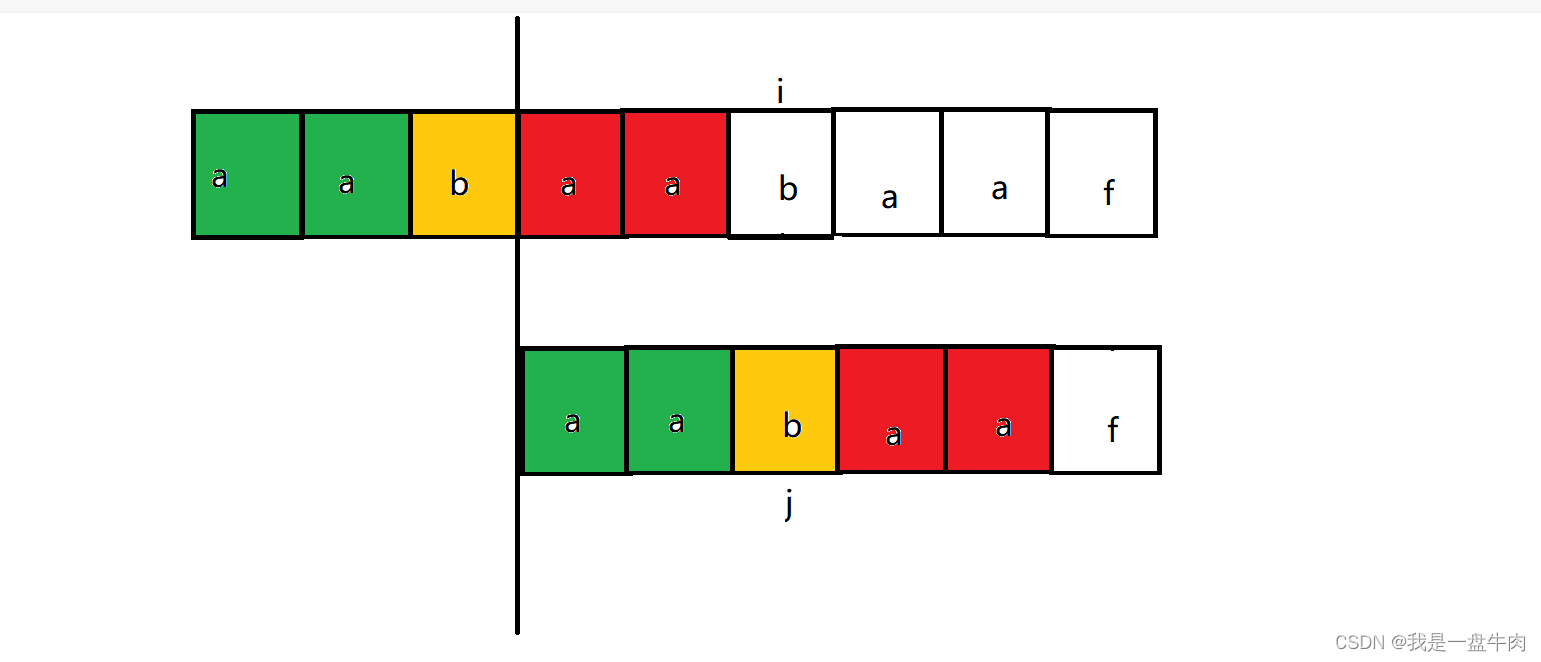
而不断的循环这种比较方法，直至找到父类中符合要求的子串，就实现了KMP算法下的字符串匹配。

通过这个我们可以总结出来模板：

每一次我们都找到不匹配字母前面的字符串（例如我们这里aabaaf中f不匹配，前置字符串就是aabaa）然后找出他的最长相等前缀后缀长度（找出有无符合上述这种红绿组合的），这里的最长相等前缀后缀是2，最后我们让i不回溯，j回退到最长相等前缀后缀位置开始向后匹配。

而next数组其实就是我们为了方便使用不匹配字母前置的字符串的最长相等前缀后缀长度，我们自己进行提前算出这个字符串的所有子串的最长相等前缀后缀长度，存储在一个数组里面方便直接使用，我们给这个把这个数组叫做next数组

需要注意的是next数组的版本多种多样，通常会对里面的数据进行各种处理。不过本质存放的都是前缀表，因此我们其实可以不对next数组做任何处理，就让他存放前缀表，依然可以实现KMP算法。

以下这句话，对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配非常重要！

下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀和后缀字符串是子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面从新匹配就可以了。

所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力。

next表的种类：

我们还是以aabaaf举例：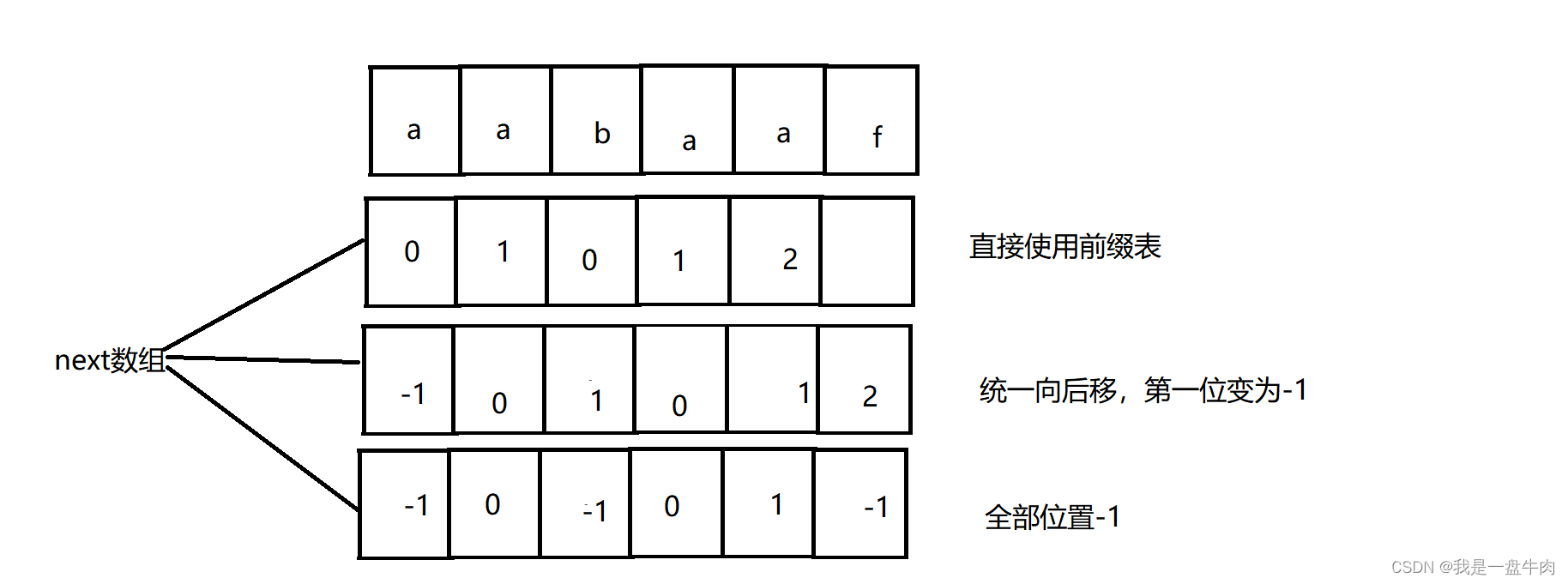

KMP算法难点：

整个KMP算法都可以看作两部分

内核：前缀表的求解，建立next数组
外壳：利用前缀表控制子字符串的回溯

主要的难点在于：如何求字符串的前缀表

其实字符串的前缀表数组计算本质上也是在运用KMP算法。

它是把字符串的前缀当作了模式串，把字符的后缀当成了文本串

void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }

KMP算法完整版：

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = 0;
        next[0] = 0;
        for(int i = 1; i < s.size(); i++) {
            while (j > 0 && s[i] != s[j]) {
                j = next[j - 1];
            }
            if (s[i] == s[j]) {
                j++;
            }
            next[i] = j;
        }
    }
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = 0;
        for (int i = 0; i < haystack.size(); i++) {
            while(j > 0 && haystack[i] != needle[j]) {
                j = next[j - 1];
            }
            if (haystack[i] == needle[j]) {
                j++;
            }
            if (j == needle.size() ) {
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};