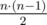深度学习笔记之Seq2seq——基于Seq2seq注意力机制的动机
引言
上一节介绍了 Seq2seq \text{Seq2seq} Seq2seq网络常用的基本结构以及在机器翻译任务中,关于目标函数与预测概率的描述。本节依然以机器翻译任务为例,对 Seq2seq \text{Seq2seq} Seq2seq中的注意力机制 ( Attention ) (\text{Attention}) (Attention)进行描述。
回顾:基于机器翻译任务的 Seq2seq \text{Seq2seq} Seq2seq网络结构
关于机器翻译任务的 Seq2seq \text{Seq2seq} Seq2seq网络结构表示如下:

该结构包含编码器
(
Encoder
)
(\text{Encoder})
(Encoder)与解码器
Decoder
\text{Decoder}
Decoder两部分。并且它们均是循环神经网络的网络结构。已知在编码器中输入的序列数据
X
\mathcal X
X表示如下:
X
=
(
x
(
1
)
,
x
(
2
)
,
⋯
,
x
(
T
)
)
T
\mathcal X = (x^{(1)},x^{(2)},\cdots,x^{(\mathcal T)})^T
X=(x(1),x(2),⋯,x(T))T
通过循环神经网络我们可以得到最终
T
\mathcal T
T时刻的序列信息
Context
\text{Context}
Context向量,记作
C
\mathcal C
C。其中
C
\mathcal C
C记录了序列数据
X
\mathcal X
X所有时刻的序列信息。
在解码器的执行过程中,初始状态下,给定一个初始标识符
⟨
Start
⟩
\left\langle\text{Start}\right\rangle
⟨Start⟩,基于
Encoder
\text{Encoder}
Encoder读取的序列信息
C
\mathcal C
C,我们可以求解翻译过程中初始时刻
y
(
1
)
y^{(1)}
y(1)的条件概率结果:
其中‘初始标识符’
⟨
Start
⟩
\left\langle\text{Start}\right\rangle
⟨Start⟩本身不包含任何语义信息。这里将其忽略;
y
(
1
)
⇒
P
(
y
(
1
)
∣
C
,
⟨
Start
⟩
)
=
P
(
y
(
1
)
∣
C
)
y^{(1)} \Rightarrow \mathcal P(y^{(1)} \mid \mathcal C,\left\langle\text{Start}\right\rangle) = \mathcal P(y^{(1)} \mid \mathcal C)
y(1)⇒P(y(1)∣C,⟨Start⟩)=P(y(1)∣C)
在得到概率分布
P
(
y
(
1
)
∣
C
)
\mathcal P(y^{(1)} \mid \mathcal C)
P(y(1)∣C)的同时,我们同样可以得到解码器初始时刻的序列信息
h
D
;
1
h_{\mathcal D;1}
hD;1:
这里以RNN \text{RNN} RNN为例,LSTM,GRU \text{LSTM,GRU} LSTM,GRU同理。只不过RNN \text{RNN} RNN的表述能够简单一些。由于⟨ Start ⟩ \left\langle\text{Start}\right\rangle ⟨Start⟩中不包含语义信息,因而不希望其对应的权重W C ⇒ h D ; 1 \mathcal W_{\mathcal C \Rightarrow h_{\mathcal D;1}} WC⇒hD;1学习到任何有用的信息,这里将其忽略。
h D ; 1 = Tanh ( W C ⇒ h D ; 1 ⋅ C + W Start ⇒ h D ; 1 ⋅ ⟨ Start ⟩ ⏟ Delete + b h D ) = Tanh ( W C ⇒ h D ; 1 ⋅ C + b h D ) \begin{aligned} h_{\mathcal D;1} & = \text{Tanh} \left(\mathcal W_{\mathcal C \Rightarrow h_{\mathcal D;1}} \cdot \mathcal C + \underbrace{\mathcal W_{\text{Start} \Rightarrow h_{\mathcal D;1}} \cdot \left\langle\text{Start}\right\rangle}_{\text{Delete}} + b_{h_{\mathcal D}}\right) \\ & = \text{Tanh}( \mathcal W_{\mathcal C \Rightarrow h_{\mathcal D;1}} \cdot \mathcal C + b_{h_{\mathcal D}}) \end{aligned} hD;1=Tanh WC⇒hD;1⋅C+Delete WStart⇒hD;1⋅⟨Start⟩+bhD =Tanh(WC⇒hD;1⋅C+bhD)
同理,根据
Seq2seq
\text{Seq2seq}
Seq2seq结构,我们同样可以得到下一时刻
y
(
2
)
y^{(2)}
y(2)的后验概率分布以及对应时刻的序列信息
h
D
;
2
h_{\mathcal D;2}
hD;2:
y
(
2
)
⇒
P
(
y
(
2
)
∣
C
,
y
(
1
)
)
h
D
;
2
=
Tanh
(
W
h
D
;
1
⇒
h
D
;
2
⋅
h
D
;
1
+
W
y
(
1
)
⇒
h
D
;
2
⋅
y
(
1
)
+
b
h
D
)
\begin{aligned} y^{(2)} & \Rightarrow \mathcal P(y^{(2)} \mid \mathcal C,y^{(1)}) \\ h_{\mathcal D;2} \ & = \text{Tanh} \left(\mathcal W_{h_{\mathcal D;1} \Rightarrow h_{\mathcal D;2}} \cdot h_{\mathcal D;1} + \mathcal W_{y^{(1)} \Rightarrow h_{\mathcal D;2}} \cdot y^{(1)} + b_{h_{\mathcal D}} \right) \end{aligned}
y(2)hD;2 ⇒P(y(2)∣C,y(1))=Tanh(WhD;1⇒hD;2⋅hD;1+Wy(1)⇒hD;2⋅y(1)+bhD)
以此类推。而最终关于生成序列
Y
\mathcal Y
Y基于
Context
\text{Context}
Context向量
C
\mathcal C
C条件下的联合概率分布
P
(
Y
∣
C
)
\mathcal P(\mathcal Y \mid \mathcal C)
P(Y∣C)可表示为:
P
(
Y
∣
C
)
=
P
(
y
(
1
)
,
y
(
2
)
,
⋯
,
y
(
T
′
)
∣
C
)
=
P
(
y
(
1
)
∣
C
)
⋅
∏
t
=
2
T
′
P
(
y
(
t
)
∣
C
,
y
(
1
)
,
⋯
,
y
(
t
−
1
)
)
\begin{aligned} \mathcal P(\mathcal Y \mid \mathcal C) & = \mathcal P(y^{(1)},y^{(2)},\cdots,y^{(\mathcal T')} \mid \mathcal C) \\ & = \mathcal P(y^{(1)} \mid \mathcal C) \cdot \prod_{t=2}^{\mathcal T'} \mathcal P(y^{(t)} \mid \mathcal C,y^{(1)},\cdots,y^{(t-1)}) \end{aligned}
P(Y∣C)=P(y(1),y(2),⋯,y(T′)∣C)=P(y(1)∣C)⋅t=2∏T′P(y(t)∣C,y(1),⋯,y(t−1))
注意力机制的动机
循环神经网络作为 Encoder \text{Encoder} Encoder产生 Context \text{Context} Context向量的缺陷
如果将解码器各输出的条件概率看做是一个复杂函数
f
(
⋅
)
f(\cdot)
f(⋅),各条件概率可表示为如下形式:
除了第一项,虽然后续函数中没有体现出
C
\mathcal C
C的参与,但实际上,解码器每一个时刻关于
y
(
t
)
(
t
=
1
,
2
,
⋯
,
T
′
)
y^{(t)}(t=1,2,\cdots,\mathcal T')
y(t)(t=1,2,⋯,T′)的生成过程均有
C
\mathcal C
C的参与,因为
h
D
;
1
,
h
D
;
2
,
⋯
h_{\mathcal D;1},h_{\mathcal D;2},\cdots
hD;1,hD;2,⋯内均有
C
\mathcal C
C参与运算。
y
(
1
)
⇒
P
(
y
(
1
)
∣
C
)
=
f
(
C
)
y
(
2
)
⇒
P
(
y
(
2
)
∣
y
(
1
)
,
C
)
=
f
(
y
(
1
)
,
h
D
;
1
)
⇒
f
(
y
(
1
)
,
C
⏟
from
h
D
;
1
)
y
(
3
)
⇒
P
(
y
(
3
)
∣
y
(
1
)
,
y
(
2
)
,
C
)
=
f
(
y
(
2
)
,
h
D
;
2
)
⇒
f
(
y
(
2
)
,
y
(
1
)
,
C
⏟
from
h
D
;
2
)
⋮
\begin{aligned} y^{(1)} & \Rightarrow \mathcal P(y^{(1)} \mid \mathcal C) = f(\mathcal C) \\ y^{(2)} & \Rightarrow \mathcal P(y^{(2)} \mid y^{(1)},\mathcal C) = f(y^{(1)},h_{\mathcal D;1}) \Rightarrow f(y^{(1)},\underbrace{\mathcal C}_{\text{from } h_{\mathcal D;1}}) \\ y^{(3)} & \Rightarrow \mathcal P(y^{(3)} \mid y^{(1)},y^{(2)},\mathcal C) = f(y^{(2)},h_{\mathcal D;2}) \Rightarrow f(y^{(2)},\underbrace{y^{(1)},\mathcal C}_{\text{from } h_{\mathcal D;2}})\\ & \quad \quad \quad \quad \quad \vdots \end{aligned}
y(1)y(2)y(3)⇒P(y(1)∣C)=f(C)⇒P(y(2)∣y(1),C)=f(y(1),hD;1)⇒f(y(1),from hD;1
C)⇒P(y(3)∣y(1),y(2),C)=f(y(2),hD;2)⇒f(y(2),from hD;2
y(1),C)⋮
因此,有:在生成
y
(
t
)
(
t
=
1
,
2
,
⋯
,
T
′
)
y^{(t)}(t=1,2,\cdots,\mathcal T')
y(t)(t=1,2,⋯,T′)的每一个时刻中,都需要对原始的原始的输入数据
X
\mathcal X
X进行读取,并生成
Context
\text{Context}
Context向量
C
\mathcal C
C。
这里描述的重点是:每生成一个
y
(
t
)
y^{(t)}
y(t),都要重新从
Encoder
\text{Encoder}
Encoder中生成一遍
C
\mathcal C
C,再对
y
(
t
)
y^{(t)}
y(t)进行翻译。
遗忘问题:但是这个过程的问题在于:由于循环神经网络梯度消失的问题,导致我们从 X \mathcal X X学习的 C \mathcal C C并不准确。这种不准确主要体现在: C \mathcal C C对 X \mathcal X X初始时刻信息存在遗忘现象。
由于梯度消失,导致C \mathcal C C仅能有效地描述最后‘若干个’时刻的序列信息,对X \mathcal X X初始时刻的序列信息,它并不能有效地记忆——长距离依赖问题。我们不否认LSTM , GRU \text{LSTM},\text{GRU} LSTM,GRU能够缓解这种问题,以GRU \text{GRU} GRU为例。以时间、空间复杂度的代价,通过‘路径’量的堆积以及‘更新门、重置门’结构的调节,使其有更多的可能将梯度传递给更深(更初始)的时刻。但是随着序列的增长,每一条路径的‘梯度消失现象’是客观存在的。
基于这种现象,可能导致:翻译出来的句子结果仅与 X \mathcal X X后半段信息存在更多关联。
对齐问题:在正常的翻译逻辑中,翻译结果与被翻译句子之间,某些词之间存在映射关系。例如:
中文:早上好。
英文:
Good morning
\text{Good morning}
Good morning.
很明显,有:
早上
⇒
morning
\Rightarrow \text{morning}
⇒morning;
好
⇒
good
\Rightarrow \text{good}
⇒good.
但是在
Context
\text{Context}
Context向量
C
\mathcal C
C作为解码器的输入,并不能很好地描述这个映射关系。换句话说:由于
C
\mathcal C
C仅仅描述的是最终时刻的序列信息,如果
C
\mathcal C
C描述的是早上好这句话的序列信息,无法将早上和好这两个词从
C
\mathcal C
C中挑选出来。
相当于这个‘固定大小的序列向量’
Context
\text{Context}
Context将每个词在句子中的序列信息‘混在一起’,单个词相关的序列信息无法‘单独拎出来’。
注意力机制处理上述两种问题
我们基于序列数据
X
\mathcal X
X学习到的序列信息,如何避免上述两种情况
?
?
?
一种直观的想法是:在学习过程中,将每一时刻的序列信息
h
(
t
)
(
t
=
1
,
2
,
⋯
,
T
)
h^{(t)}(t=1,2,\cdots,\mathcal T)
h(t)(t=1,2,⋯,T)都存储下来:
x
(
t
)
→
h
(
t
)
⇒
X
→
H
=
(
h
(
1
)
,
h
(
2
)
,
⋯
,
h
(
T
)
)
T
x^{(t)} \rightarrow h^{(t)} \Rightarrow \mathcal X \rightarrow \mathcal H = (h^{(1)},h^{(2)},\cdots,h^{(\mathcal T)})^T
x(t)→h(t)⇒X→H=(h(1),h(2),⋯,h(T))T
此时在解码过程中不再使用最终
T
\mathcal T
T时刻序列信息作为
Context
\text{Context}
Context向量
C
\mathcal C
C了,因为上述两种问题
C
\mathcal C
C无法解决。随之而来的是各时刻序列信息组成的矩阵
H
\mathcal H
H,新的问题随之出现:如何使用
H
\mathcal H
H取描述/确定
Context
\text{Context}
Context向量
C
?
\mathcal C ?
C?
例如如下的翻译例子:
中文:我 是 一名 演员。
期望的翻译结果:
英文:
I am an actor
\text{I am an actor}
I am an actor.
首先观察 am \text{am} am这个词,它在编码前的中文对应的是这个词,也就是说:是这个词对翻译结果 am \text{am} am的作用很大。另一个问题:翻译结果为 am \text{am} am,对这个翻译结果产生贡献的仅仅只有[是]这一个词吗 ? ? ?
在这里明显不是。 am \text{am} am在英语中是 be \text{be} be动词的一种,一般用来表示[是]这个意思, be \text{be} be动词有好多种( am,is,are,was,were , ⋯ \text{am,is,are,was,were},\cdots am,is,are,was,were,⋯),为什么这里要选择 am ? \text{am}? am?因为:输入的序列数据 X \mathcal X X中是第一人称——[我]。
假设从重要程度的角度观察,翻译结果
am
\text{am}
am关于输入序列数据
X
\mathcal X
X中各词的重要程度表示如下:
这里的‘重要程度’
0.3
,
0.7
0.3,0.7
0.3,0.7是假设的结果。

这仅仅是从句子逻辑的角度考虑的,那换成向量呢
?
?
?由于
h
(
1
)
,
h
(
2
)
,
⋯
h
(
T
)
∈
H
h^{(1)},h^{(2)},\cdots h^{(\mathcal T)} \in \mathcal H
h(1),h(2),⋯h(T)∈H中,
h
(
t
)
h^{(t)}
h(t)所包含的序列信息也包含前面
t
−
1
t-1
t−1个时刻的序列信息,只不过因遗忘的因素存在,
t
t
t值越来越大,初始时刻保留的信息越来越少而已。将上述信息用向量进行表示,具体的重要程度分布表示如下:
这里比例设置得可能不太平衡,这仅是一个示例。

至此,可以认为:解码器预测的结果是基于编码器各时刻隐状态的共同结果,只不过不同隐状态对应的权重比率不同而已。从而针对这些向量进行加权求和:
C
2
=
C
am
⇒
0.2
∗
h
(
1
)
+
0.7
∗
h
(
2
)
+
0.05
∗
h
(
3
)
+
0.03
∗
h
(
4
)
+
0.02
∗
h
(
5
)
\mathcal C_2 = \mathcal C_{\text{am}} \Rightarrow 0.2 * h^{(1)} + 0.7 * h^{(2)} + 0.05 * h^{(3)} + 0.03 * h^{(4)} + 0.02 * h^{(5)}
C2=Cam⇒0.2∗h(1)+0.7∗h(2)+0.05∗h(3)+0.03∗h(4)+0.02∗h(5)
这种基于加权求解解码器输出的方式相比于之前之前所有输出均基于
Context
\text{Context}
Context向量
C
\mathcal C
C的方式而言,能够得到更有注意力偏向的结果。
这里同样可以例举一个
an
\text{an}
an的例子。
an
\text{an}
an是不定冠词,为什么不选择
a
\text{a}
a而是选择
an
\text{an}
an——很明显,其后面第一个词是
actor
\text{actor}
actor,开头是元音字母。因此
an
\text{an}
an的生成从句子角度观察与[一名],[演员]两个词都有关联关系,这里就不展开描述了。
两者最明显的区别在于:每一个词均有不同的注意力偏向,即不同的
Context
\text{Context}
Context向量与其对应
(
C
1
,
C
2
,
⋯
)
(\mathcal C_1,\mathcal C_2,\cdots)
(C1,C2,⋯)。从而不再共用同一个
Context
\text{Context}
Context向量
C
\mathcal C
C:
这里两种方式做一个比对。
{
y
(
1
)
=
f
(
C
)
y
(
2
)
=
f
(
y
(
1
)
,
C
)
y
(
3
)
=
f
(
y
(
1
)
,
y
(
2
)
,
C
)
⋮
⟺
{
y
(
1
)
=
f
(
C
1
)
y
(
2
)
=
f
(
y
(
1
)
,
C
2
)
y
(
3
)
=
f
(
y
(
1
)
,
y
(
2
)
,
C
3
)
⋮
\begin{aligned} \begin{cases} y^{(1)} & = f(\mathcal C) \\ y^{(2)} & = f(y^{(1)},\mathcal C) \\ y^{(3)} & = f(y^{(1)},y^{(2)},\mathcal C) \\ & \vdots \\ \end{cases} \Longleftrightarrow \begin{cases} y^{(1)} & = f(\mathcal C_1) \\ y^{(2)} & = f(y^{(1)},\mathcal C_2) \\ y^{(3)} & = f(y^{(1)},y^{(2)},\mathcal C_3) \\ & \vdots \\ \end{cases} \end{aligned}
⎩
⎨
⎧y(1)y(2)y(3)=f(C)=f(y(1),C)=f(y(1),y(2),C)⋮⟺⎩
⎨
⎧y(1)y(2)y(3)=f(C1)=f(y(1),C2)=f(y(1),y(2),C3)⋮
权重系数求解
针对上面描述,我们确定了针对不同的解码输出,从而对编码部分构建不同的注意力偏向。问题在于:这个偏向,也就是各时刻序列信息的权重系数/权重比例如何求解:
依然以上面的我 是 一名 演员 。 ⇒ I am an actor . \Rightarrow \text{I am an actor .} ⇒I am an actor .为例。假设 t = 2 t=2 t=2时刻要预测 am \text{am} am这个单词,如何给原始各时刻的序列信息 h ( 1 ) , h ( 2 ) , h ( 3 ) , h ( 4 ) , h ( 5 ) h^{(1)},h^{(2)},h^{(3)},h^{(4)},h^{(5)} h(1),h(2),h(3),h(4),h(5)分配权重 ? ? ?
一种朴素的想法:
- 在解码过程的 t ( t = 1 , 2 , ⋯ , T ′ ) t(t=1,2,\cdots,\mathcal T') t(t=1,2,⋯,T′)时刻,选择该时刻的一个向量 Q t \mathcal Q_t Qt;
- 让 Q t \mathcal Q_t Qt分别与编码器各时刻的序列信息 h ( i ) ( i = 1 , 2 , ⋯ , T ) h^{(i)}(i=1,2,\cdots,\mathcal T) h(i)(i=1,2,⋯,T)进行比较,计算它们之间的相似度结果 Score ( Q t , h ( i ) ) \text{Score}(\mathcal Q_t,h^{(i)}) Score(Qt,h(i)),相似度高的 Score \text{Score} Score数值更大;
- 最终将个 Score \text{Score} Score结果做一个归一化操作即可。
基于这种想法,关于解码器的 t t t时刻,此时 y ( t ) y^{(t)} y(t)还没有被预测出来,那么选择哪一个向量作为 Q t \mathcal Q_t Qt与 h ( i ) ( i = 1 , 2 , ⋯ , T ) h^{(i)}(i=1,2,\cdots,\mathcal T) h(i)(i=1,2,⋯,T)进行比较呢 ? ? ?
两种思路:
- 将解码器中当前 t t t时刻的上一时刻( t − 1 t-1 t−1)的隐状态 h D ; t − 1 h_{\mathcal D;t-1} hD;t−1作为 Q t \mathcal Q_t Qt;
- 将解码器中当前 t t t时刻的隐状态 h D ; t h_{\mathcal D;t} hD;t作为 Q t \mathcal Q_t Qt;
无论 Q t \mathcal Q_t Qt使用哪种选择方式,都被称作查询向量 ( Query ) (\text{Query}) (Query)。这里首先介绍 Score ( Q t , h ( i ) ) \text{Score}(\mathcal Q_t,h^{(i)}) Score(Qt,h(i))的计算方式。
Score \text{Score} Score函数的计算方式
计算两向量之间的相似度,最先想到的就是余弦相似度
(
Cosine Similarity
)
(\text{Cosine Similarity})
(Cosine Similarity)。具体做法就是两向量之间做内积:
M
T
N
=
(
m
1
,
m
2
,
⋯
m
k
)
(
n
1
n
2
⋮
n
k
)
=
m
1
n
1
+
m
2
n
2
+
⋯
+
m
k
n
k
M
,
N
∈
R
k
×
1
\mathcal M^T\mathcal N = (m_1,m_2,\cdots m_k) \begin{pmatrix} n_1 \\ n_2 \\ \vdots \\ n_k \end{pmatrix} = m_1n_1 + m_2n_2 + \cdots + m_kn_k \quad \mathcal M,\mathcal N \in \mathbb R^{k \times 1}
MTN=(m1,m2,⋯mk)
n1n2⋮nk
=m1n1+m2n2+⋯+mknkM,N∈Rk×1
内积数值越大,意味着两向量的相似性程度越高;我们仅需要将解码器产生的查询向量
Q
t
\mathcal Q_t
Qt(例如:
h
D
;
t
h_{\mathcal D;t}
hD;t)与编码器中各时刻产生的序列信息
h
(
i
)
(
i
=
1
,
2
,
⋯
,
T
)
h^{(i)}(i=1,2,\cdots,\mathcal T)
h(i)(i=1,2,⋯,T)进行内积即可。
但这种操作的问题在于:需要 Q t \mathcal Q_t Qt与 h ( i ) h^{(i)} h(i)之间的张量格式相同,否则无法执行内积。这里的张量格式具体指什么 ? ? ?不可否认的是: Seq2seq \text{Seq2seq} Seq2seq模型结构中的 Encoder \text{Encoder} Encoder和 Decoder \text{Decoder} Decoder是两个独立的循环神经网络结构。这里以单层 GRU \text{GRU} GRU神经网络为例:
已知某 Batch \text{Batch} Batch的数据格式为: [ 100 , 10 , 8 ] [100,10,8] [100,10,8]。其中:
- 100 100 100表示 BatchSize \text{BatchSize} BatchSize大小;
- 10 10 10表示文本的序列长度;
- 8 8 8表示每个词的 Embedding \text{Embedding} Embedding维数;
关于 GRU \text{GRU} GRU的参数描述: EmbedSize = 8 \text{EmbedSize = 8} EmbedSize = 8;就是词语的 Embedding \text{Embedding} Embedding维数; NumHiddens= 16 \text{NumHiddens= 16} NumHiddens= 16;(这里随意选择的值)表示神经元个数,但是这个参数和输出的序列长度,或者是 RNN \text{RNN} RNN的循环次数之间没有任何关系。
在 Seq2seq \text{Seq2seq} Seq2seq基本介绍中提到过,循环神经网络输入与输出的序列长度相同。这也是它无法直接做机器翻译的弊端。同理, NumLayers = 2 \text{NumLayers = 2} NumLayers = 2表示如果是深度循环神经网络,该参数描述神经网络堆叠的层数。观察上述格式数据,进入 GRU \text{GRU} GRU网络后的输出结果:
import torch
from torch import nn as nn
BatchSize = 100
SeqLength = 10
EmbedSize = 8
NumHiddens = 16
NumLayers = 2
x = torch.randn(BatchSize,SeqLength,EmbedSize).permute(1,0,2)
RNN = nn.GRU(EmbedSize,NumHiddens,NumLayers)
Output,State = RNN(x)
print(x.shape)
print(Output.shape,State.shape)
返回结果如下:
torch.Size([10, 100, 8])
torch.Size([10, 100, 16]) torch.Size([2, 100, 16])
可以看出,关于单个时刻的序列信息
State
\text{State}
State,影响它格式的有
NumLayers,NumHiddens
\text{NumLayers,NumHiddens}
NumLayers,NumHiddens,但绝对不会有序列长度相关的信息进行影响。
为什么要强调这个~是因为视频中存在一些偶然情况,导致理解错误。
由于是两个独立的循环结构,不同的网络参数也会影响各自
State
\text{State}
State输出的张量格式,从而导致无法直接求解内积。
这里介绍两种解决方式:
- 既然
Q
t
\mathcal Q_t
Qt与
h
(
i
)
h^{(i)}
h(i)之间的张量格式不匹配,通过乘以一个参数矩阵
W
Q
t
\mathcal W_{\mathcal Q_t}
WQt,从而使他们的格式匹配,从而进行内积。例如:
为简化起见,仅使用一个样本进行描述。即BatchSize=1 \text{BatchSize=1} BatchSize=1并消掉维度;并且NumLayers = 1 \text{NumLayers = 1} NumLayers = 1,主要观察NumHiddens \text{NumHiddens} NumHiddens之间的区别。其中N E n \mathcal N_{En} NEn表示编码器Encoder \text{Encoder} Encoder的NumLayers \text{NumLayers} NumLayers;N D e \mathcal N_{De} NDe表示Decoder \text{Decoder} Decoder的NumLayers \text{NumLayers} NumLayers。
{ Q t ∈ R N E n × 1 , h ( i ) ∈ R N D e × 1 W Q t ∈ R N E n × N D e ⇒ [ W Q t ] T Q t ∈ R N D e × 1 \begin{cases} \mathcal Q_t \in \mathbb R^{\mathcal N_{En} \times 1},h^{(i)} \in \mathbb R^{\mathcal N_{De} \times 1} \\ \mathcal W_{\mathcal Q_t} \in \mathbb R^{\mathcal N_{En} \times \mathcal N_{De}}\Rightarrow [\mathcal W_{\mathcal Q_t}]^T \mathcal Q_t \in \mathbb R^{\mathcal N_{De} \times 1} \end{cases} {Qt∈RNEn×1,h(i)∈RNDe×1WQt∈RNEn×NDe⇒[WQt]TQt∈RNDe×1
在降维中介绍过,这实际上就是一种‘特征转换’:将原始向量(未丢失信息)从当前特征空间映射到高维/低维特征空间。基于映射情况来调整W Q t \mathcal W_{\mathcal Q_t} WQt内向量间的关系。
最终的内积结果可表示为如下形式:该结果就是编码器 t t t时刻的序列信息 Q t \mathcal Q_t Qt与解码器 i i i时刻的生成序列信息 h ( i ) h^{(i)} h(i)的相似度结果。
Score ( Q t , h ( i ) ) = [ [ W Q t ] T Q t ] T h ( i ) = [ Q t ] T W Q t h ( i ) \text{Score}(\mathcal Q_t,h^{(i)})= \left[[\mathcal W_{\mathcal Q_t}]^T \mathcal Q_t\right]^T h^{(i)} = [\mathcal Q_t]^T \mathcal W_{\mathcal Q_t} h^{(i)} Score(Qt,h(i))=[[WQt]TQt]Th(i)=[Qt]TWQth(i) - 另一种方式就是构建神经网络。将两向量拼接
(
Concatenate
)
(\text{Concatenate})
(Concatenate)在一起作为神经网络的输入信息;根据神经网络的通用逼近定理
(
Universal Approximation Theorem
)
(\text{Universal Approximation Theorem})
(Universal Approximation Theorem),使其结果返回
Score
\text{Score}
Score作为输出。
需要训练的参数就是神经网络中神经元对应的权重信息。
两种方式的主要区别在于:
- 内积方法是从余弦相似度的角度出发,虽然中间使用 W \mathcal W W执行特征转换,但其结果依然可以表达 Q t \mathcal Q_t Qt和 h ( i ) h^{(i)} h(i)之间的相关关系;
- 而神经网络方法则全权交给通用逼近定理了,无法体现出 Q t \mathcal Q_t Qt与 h ( i ) h^{(i)} h(i)之间的相关关系。
相关参考:
seq2seq与attention机制