第三次题组 [Cloned] - Virtual Judge (vjudge.net)

 【题目描述】

一个具有 n 个顶点和 m 条边的无向图。现在，世界上最好的头脑即将确定这张图是否可以被视为克苏鲁。

为了简单起见，让我们假设克苏鲁从空间里看起来就像一个附有触手的球形身体。从形式上讲，我们将把这样的无向图视为克苏鲁，它可以表示为一组三棵或更多根树，其根通过一个简单的循环连接起来。

保证图形不包含多条边和自循环。

【输入】

第一行包含两个整数 — 图形的顶点数 n 和边数 m （1 ≤ n ≤ 100， 0 ≤ m ≤ 

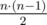
以下 m 行中的每一条都包含一对整数 x 和 y，它们表明顶点 x 和 y 之间存在一条边（1 ≤ x、y ≤ n、 x ≠ y）。对于每对顶点，它们之间最多只有一条边，没有边将顶点连接到自身。

【输出】

如果图表不是克苏鲁，请打印“NO”，如果是，则打印“FHTAGN！

解题思路

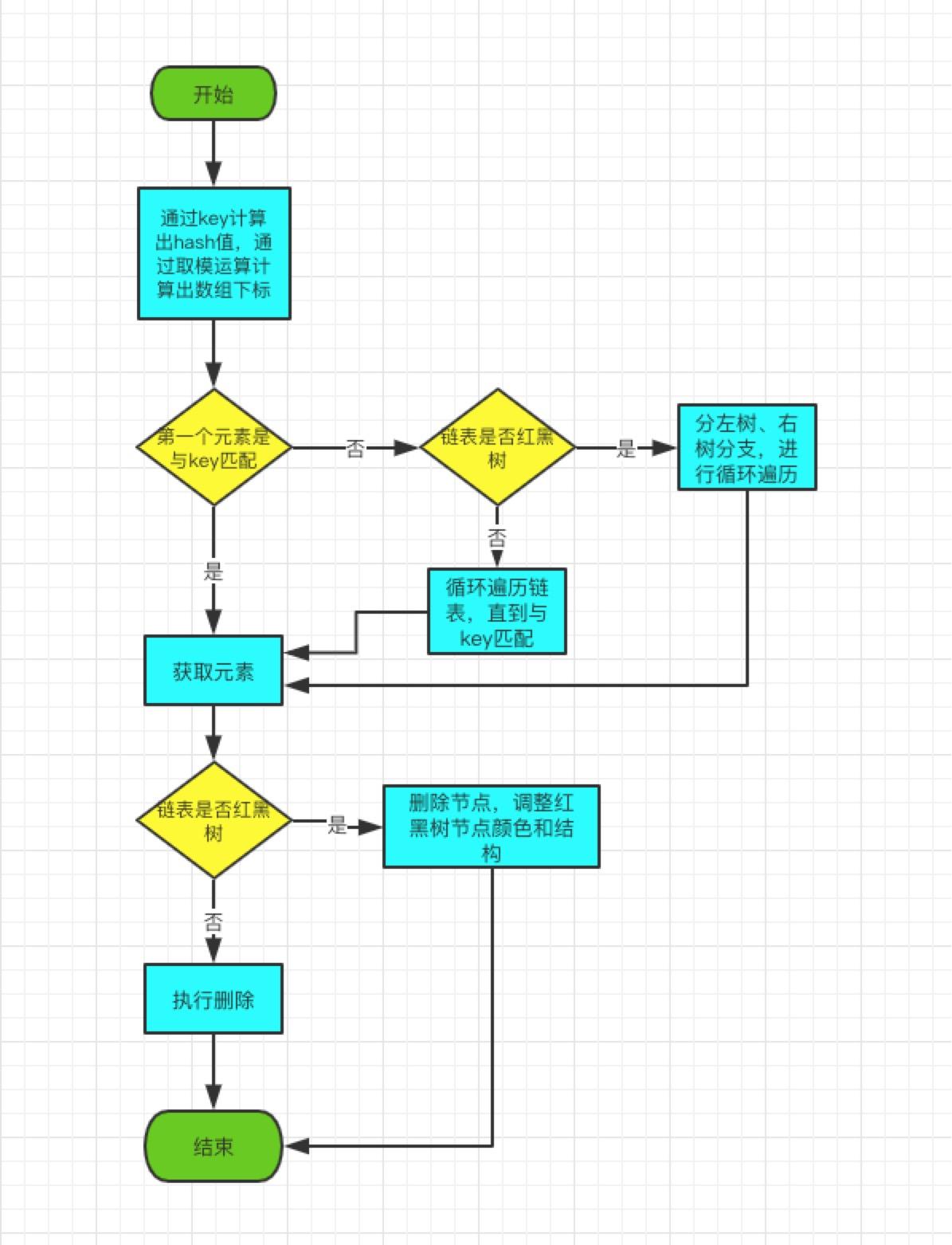
这个题是用到并查集。

并查集数组f[n]，要注意在使用之前初始化，将f[i]=i，作用是：未连接边时，每个顶点的首领结点是它自己，f[i]中的i是当前的结点序号，赋值的i是它的首领结点编号。

题意大概是：将输入的信息连接为一张无向图，其中连接的无向图如果满足：只包含一个回路，回路上的任意顶点都可以延展出去。

1、在连接边的时候，用并查集判读是否形成回路， 如果形成了回路，判断这个形成的回路是否是第一个形成的回路。

2、题目中给到的点，必须全部用边连接，所以用一个计数器统计连接的边数（因为可能会出现重复连接的边，或边数不足以连接的情况）

3、没有回路的情况也需要判断，所以用了两个标记：flag和flag2

代码如下

#include <iostream>
#include <stdio.h>
using namespace std;
int f[1010];
//并查集
int find(int x)
{
    if (f[x] == x)
        return x;
    else
        return  find(f[x]);
}

int main()
{
    int n, m;
    cin >> n >> m;
    //初始化f数组
    for (int i = 1; i <= n; i++)
        f[i] = i;
    int flag, a, b, num, flag2;
    flag = num = flag2 = 0;
    for (int i = 0; i < m; i++) {
        cin >> a >> b;
        int px = find(a), py = find(b);
        //两个点还未形成通路的情况
        if (px != py) {
            num++;
            f[px] = py;
        }
        //连接当前的点形成了回路，接下来判断这个回路是是形成的第一个回路还是第二个回路
        else {
            //如果flag==0，说明先前未形成回路，当前形成的是第一个回路
            if (flag==0) {
                num++;
                flag = 1;
            }
            //如果是形成的第二个回路，将flag2赋为1，结束循环，此时能判断肯定是输出no
            else{
                flag2 = 1;
                break;
            }
        }
    }
    if (!flag2 && flag && num == n)
        cout << "FHTAGN!";
    else
        cout << "NO";
    return 0;
}