前言

建立空间计量模型的前提，一般要引入空间权重矩阵$W$来表达$n$个位置的空间区域邻近关系。
但空间权重矩阵的构造一直是备受争议的，理论是不存在最优的空间矩阵，那么在实证分析中，通常用一个词总结试一试。下文总结了目前研究中所有的空间权重矩阵。

1.邻接矩阵

空间矩阵的常规设定有两种，一个是 简单二进制邻接矩阵，按照国际响起规则，顾名思义相邻（共边）为1，反之为0.
$W[i][j]=1$，如果地理单元$i$与地理单元$i$相邻或存在连接；
$W[i][j]=0$，如果地理单元$i$与地理单元$j$不相邻或不存在连接。

2.基于距离的空间邻接矩阵

这是按照
$W[i][j]=1$，如果地理单元$i$与地理单元$i$当区域$i$的距离小于d时；
$W[i][j]=0$，其他。
表示地理单元$i$与地理单元$j$之间的权重，其中$d[i][j]$是地理单元$i$与地理单元$j$之间的距离。

3.基于万有引力定律的空间邻接矩阵

此矩阵用于区域贸易问题，由诺贝尔经济学家Tingbergen提出。

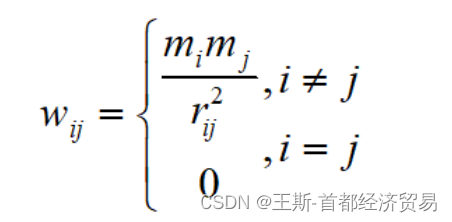
$m_i$表示表示$i$地区的经济实力，$r_{ij}$地区$i$和$j$的地理距离。

4.基于地理距离标准构造空间权重矩阵

基于地理学第一定律建立，即任何事物与其他周围事物之间均存在一定联系，而距离较远的事物总比距离较远的事物联系更加紧密。

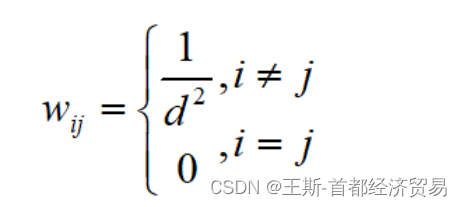
$d$表示两地区地理中心位置之间的距离。

5.社会经济特征空间权重矩阵（经济距离空间权重矩阵）

基于地理的权重矩阵反映的空间联系较为粗糙，还应该考虑非地理邻近因素。值得注意的是，注意两单元之间的相互强度影响（理解：班级中，好的同学带动差的同学成绩提升作用与差的同学给好的同学反馈作用是不对等的），

$$W=W_{d}diag(\frac{{\overline{Y}}_1}{\overline{Y}},\frac{{\overline{Y}}_2}{\overline{Y}},\frac{{\overline{Y}}_3}{\overline{Y}},\dots ,\frac{{\overline{Y}}_n}{\overline{Y}})$$

$W_d$为地理距离空间权重矩阵。$\overline{Y_i}=\frac{1}{t_1-t_0+1}{\sum }_{t=t_0}^{t_1}{Y}_{it}$,$\overline{Y}=\frac{1}{n(t_1-t_0+1)}{\sum }_{i=1}^n{\sum }_{t=t_0}^{t_1}{Y}_{it}$。

6.竞争矩阵

通常，基础设施建设可能存在一定的正负溢出效应。
构造的竞争矩阵空间权重为：
$$$d_{ij}=\sqrt{{\sum }_m(a_{im}-a_{jm}{)}^2}$
$a_{im}$ 表示省份$i$的产业$m$占制造业产值比重。

7.其他

• Queen 近邻权重矩阵：表示单元周围 8 个方向的相邻单元都有权重值，采用一个正方形相邻计算范围。
• Rook 近邻权重矩阵：仅考虑单元周围 4 个方向的相邻单元，采用一个正方形相邻计算范围。
• Distance 权重矩阵：单元之间的权重取决于它们之间的距离远近，一般采用欧式距离、曼哈顿距离等方式计算。
• Kernel 权重矩阵：将每个单元周围的相邻单元权重分配一个权值，常用Gaussian（高斯核）、Epanechnikov核权重等。