前言

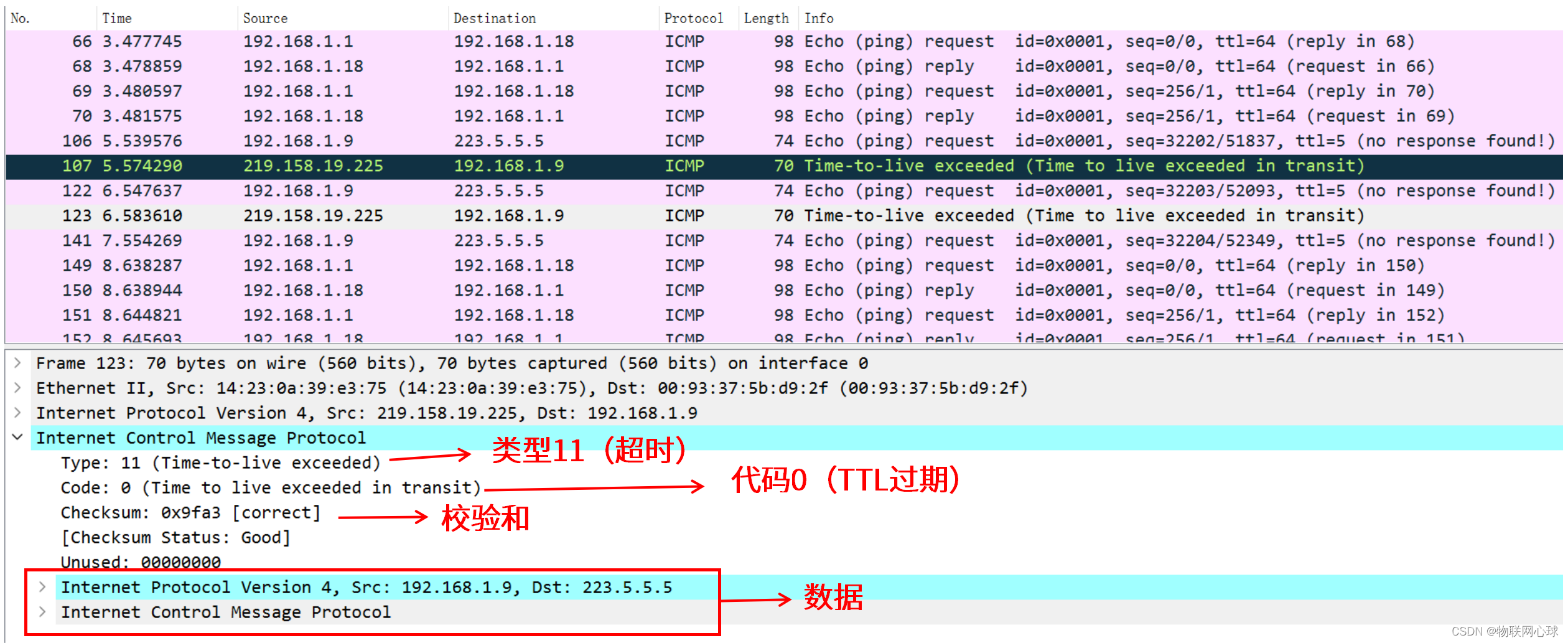
当前空间计量模型的实证研究中，国内的文献均是基于LM检验的空间自相关和空间误差模型进行选择与分析，但是LM检验确实存在局限性。故此，需要对空间计量模型选择进行一个阐述。下列出现在空间计量模型选择方法。

原理	方法
基于统计检验方法	Moran指数检验、LM检验
基于极大似然方法	AIC、BIC、HQC、QAIC
基于模型后验概率的贝叶斯选择方法
基于MCMC的空间计量模型选择方法

1.Moran指数检验

Moran指数反映空间邻接与邻近单元的相似程度，即空间相关性。
$H_o=模型不存在空间相关性$
局限：只用于检验空间相关性，无法确定是空间自回归还是空间残差相关。
结论：Moran方法并不能起选择模型的作用。

衍生知识：

• 莫兰指数分为全局莫兰指数（GlobalMoran’s I）和安瑟伦局部莫兰指数（AnselinLocal Moran’s I）
• Moran’s I >0表示空间正相关性，其值越大，空间相关性越明显。Moran’s I <0表示空间负相关性，其值越小，空间差异越大，否则，Moran’s I = 0，空间呈随机性。
• 
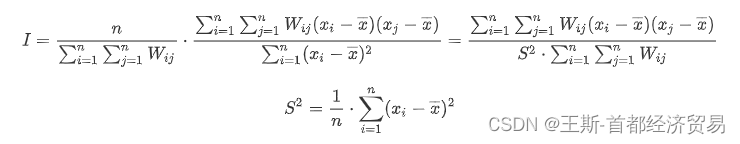
  $n$区域空间单元总数
  $W$权重矩阵
  $X$变量
  $S^2$变量方差
  ​
  为地理单元相互之间邻接关系的权重矩阵。空间权重矩阵可以根据邻接标准或距离标准来度量，邻接标准将空间单元的1，把不连接的定义为0。距离标准是根据一定范围内的定义为1，把距离之外的定义为0。

Geary’s C指数

Geary’s C指数也是全局聚类检验的一个指数。
Geary’s C指数的形式和莫兰指数很相似，区别主要在于交叉乘积项不同：Moran’s I的交叉乘积项为，Geary’s C的交叉乘积项为；
Geary’s C指数的范围在0-2之间，其中0 < C<1表示正相关，1<C<2表示负相关。

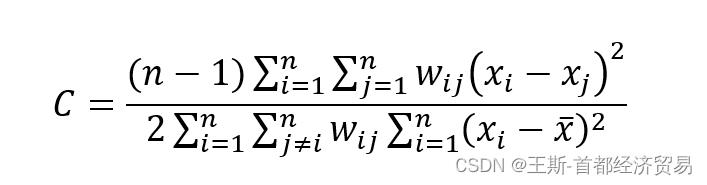
2.LM检验

这是个基于LM的检验统计量如下：

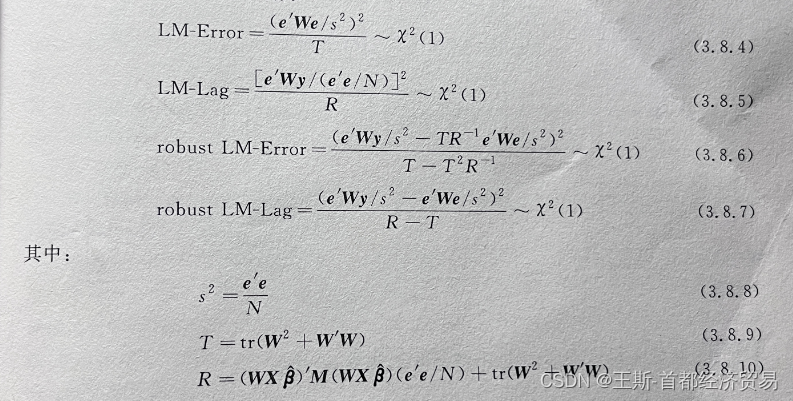
• 1.LM-Error统计量，不存在空间自回归时空间残差相关的LM检验。原假设，是模型残差不存在空间相关。
• 2.LM-Lag统计量，不存在空间残差相关时空间自回归效应的LM检验，原假设，是模型残差不存在空间相关。
• 3.Robust LM-Error统计量-存在空间自回归时，空间残差相关的LM检验，原假设，是模型仍然是残差不存在空间相关。
• 4.Robust LM-Lag统计量，存在空间残差相关性时空间自回归效应的LM检验,原假设，是模型仍然是残差不存在空间相关。

例子:
为确定是使用空间滞后模型SLM还是空间误差模型SEM，需要进行模型的选择。先采用最小二乘法（OLS）对模型进行估计，然后比较拉格朗日乘数LM的显著性。如果LM-lag统计上的显著性高于LM-error，同时，Robust LM-lag显著性高于Robust LM-error，则使用空间滞后模型SLM。反之，LM-lag统计上的显著性低于LM-error，同时，Robust LM-lag显著性低于Robust LM-error，则使用空间误差模型SEM。

选择流程图：

3.基于信息准则的空间计量模型选择方法

3.1 赤池信息准则：AIC

$$AIC=-2ln(L)+2k$$
$ln(L)$极大对数似然函数，$k$参数个数。AIC越小越好。

3.1 贝叶斯信息准则：BIC

$$BIC=-2ln(L)+k\ast ln(n)$$
$n$样本量。AIC越小越好。

3.1 Hannan-Quinn准则：HQ

$$HQ=-2ln(L)+k\ast ln[ln(n)]$$
注意，HQ和BIC类似，选择的模型比AIC更加精简。

3.1 数据过度离散情况下的信息准则：QAIC

$$QAIC=2k-\frac{2}{VIF}ln(L)$$
小样本下
$$QA{K}^{{}^{\prime }}=QAIC+\frac{2k(k+1)}{n-k-1}$$
$VIF$方差膨胀因子。

4.基于模型后验概率的贝叶斯选择方法

利用似然比的方法选择模型，计算后验机会比，具体的推导过程略。
此方法在对边际似然函数计算难度较大。

5.基于MCMC的空间模型选择方法

此方法用于估计复杂的计量模型，比如带未知异方差的广义空间模型。（看不懂!）