一、树与图的深度优先遍历

数与图的深度优先遍历与 DFS 类似，将树与图的各条分支给依次遍历一遍。其核心思想依然是递归，但是遍历对象变成了无向图。

1. 构造

由于是无向图，它构建起来不同于普通的树，代码如下：

int e[N],ne[N],h[M];//M = 2 * N;
int idx;

void add(int a,int b)
{
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

在输入时：

int a,int b;
cin >> a >> b;
add(a,b),add(b,a);

由于是无向图，所以要 add 两次，如果是有向图，只需要按指向进行 add 即可。
add 函数与单链表插入头节点的函数类似，下面是单链表插入头节点的代码：

void head_add(int x)
{
    e[idx] = x,ne[idx] = head,head = idx++;  
}

仅仅将 head 换成了 h 数组。
而在无向图当中，h 和 ne 数组发挥的作用是不同的。h 是指向子节点的指针，用于递归部分，而 ne 搜索到结束时跳转回上一个分叉的零一个子节点的指针，用于循环。

2. 遍历

如下所示的 DFS 函数框架代码：

void dfs(int u){
    st[u]=true; // 标记一下，记录为已经被搜索过了，下面进行搜索过程
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        if(!st[j]) 
        {
            dfs(j);
        }
    }
}

3. 具体实现详见例题——树的重心

二、树与图的深度优先遍历例题——树的重心

题目描述

给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。
请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。
重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数 n，表示树的结点数。
接下来 n−1 行，每行包含两个整数 a 和 b，表示点 a 和点 b 之间存在一条边。

输出格式

输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围

1 ≤ n ≤ 1e5

输入样例

9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6

输出样例

4

具体实现

1. 样例演示

1 到 2 连一条边。
1 到 7 连一条边。
1 到 4 连一条边。
2 到 8 连一条边。
2 到 5 连一条边。
4 到 3 连一条边。
3 到 9 连一条边。
4 到 6 连一条边。
得到如下图所示的树：

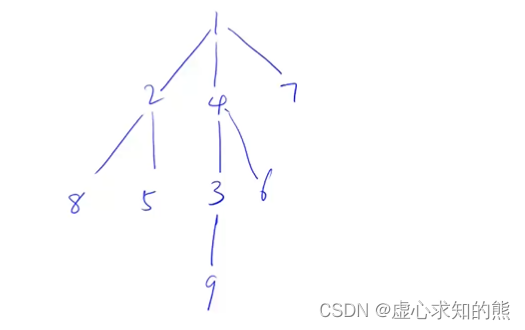
在这里插入图片描述

然后，我们依次遍历删除每一个节点，取出每次删除后的最大值，进行比较，得出其中的最小值输出。
当我们删除 1 号点，便得到了三个连通块，分别为 { 2，5，8 } ，{ 4，5，6，9 }，{ 7 } 。其中，最多的点数是 4 。
后续过程同理。

2. 实现思路

首先，我们需要弄清楚题目当中树的重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。
这里需要注意的是，这里输出的不是重心编号，而是输出各个连通块中点数最小的最大值是多少，因为树的重心可能不唯一，但是这个数字是唯一的，通过这个数字比较好评测。
在此，我们只需要在删除一个点后，从下往上统计其对应子节点所在连通块中点的个数和其上面父节点所在连通块中点的个数，然后进行比较即可。
以删除 4 号点为例：

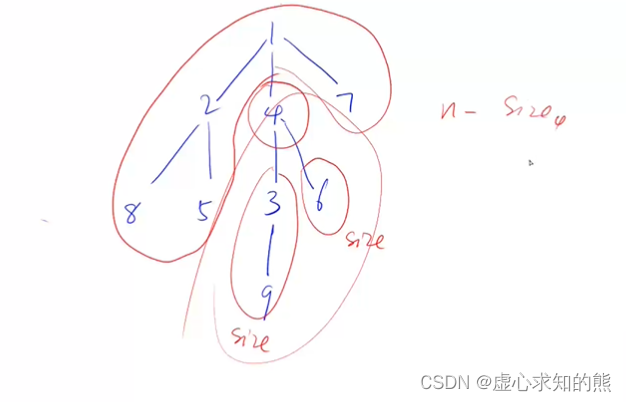
在这里插入图片描述

3. 代码注解

bool st[N]；用于记录每个点是否被使用过。
节点的编号是指上图所画的树中节点的值，范围是从1~n 。在本题中，每次输入的 a 和 b 就是节点的编号，编号用 e[i] 数组存储。
节点的下标指节点在数组中的位置索引，数组之间的关系就是通过下标来建立连接，下标用 idx 来记录。 idx 范围从 0 开始，如果 idx==-1 表示空。
详细注解在代码中标注了。

4. 实现代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10; //数据范围是10的5次方
const int M = 2 * N; //以有向图的格式存储无向图，所以每个节点至多对应2n-2条边

int h[N]; //邻接表存储树，有n个节点，所以需要n个队列头节点
int e[M]; //存储元素
int ne[M]; //存储列表的next值
int idx; //单链表指针
int n; //题目所给的输入，n个节点
int ans = N; //表示重心的所有的子树中，最大的子树的结点数目

bool st[N]; //记录节点是否被访问过，访问过则标记为true

//a所对应的单链表中插入b  a作为根 
void add(int a, int b) 
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

//返回以u为根的子树中节点的个数，包括u节点
int dfs(int u) 
{
    int res = 0; //存储 删掉某个节点之后，最大的连通子图节点数
    st[u] = true; //标记访问过u节点
    int sum = 1; //存储 以u为根的树 的节点数, 包括u，如图中的4号节点

    //访问u的每个子节点
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        //因为每个节点的编号都是不一样的，所以用编号为下标 来标记是否被访问过
        if (!st[j])
        {
            int s = dfs(j);  // u节点的单棵子树节点数，如图中的size值
            res = max(res, s); // 记录最大联通子图的节点数
            sum += s; //以j为根的树 的节点数
        }
    }

    //n-sum 如图中的n-size值，不包括根节点4；
    res = max(res, n - sum); // 选择u节点为重心，最大的 连通子图节点数
    ans = min(res, ans); //遍历过的假设重心中，最小的最大联通子图的 节点数
    return sum;
}

int main()
{
    memset(h, -1, sizeof h); //初始化h数组 -1表示尾节点
    cin >> n; //表示树的结点数

    // 题目接下来会输入，n-1行数据，
    // 树中是不存在环的，对于有n个节点的树，必定是n-1条边
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a); //无向图
    }

    dfs(1); //可以任意选定一个节点开始 u<=n

    cout << ans << endl;
    system("pause");
    return 0;
}