Deep Gradient Projection Networks for Pan-sharpening

（用于全色锐化的深度梯度投影网络）

全色锐化是遥感成像系统获取高分辨率多光谱图像的重要技术。最近，深度学习已经成为最流行的泛锐化工具。提出了一种基于模型的深度全色锐化方法。具体地说，提出了两个由深度先验正则化的优化问题，它们分别负责全色图像和低分辨率多光谱图像的生成模型。然后，利用梯度投影算法求解这两个问题，并将迭代步骤推广到两个网络块中。通过交替叠加这两个块，构造了一种新的网络，称为基于梯度投影的全色锐化神经网络。

介绍

多光谱图像（MS）存储多图像对应于光谱中的每个波段（或者说，通道），并且它们在遥感文献中被广泛使用。然而，由于成像设备的限制，卫星通常测量低空间分辨率多光谱（LRMS）图像。与多光谱影像相比，全色影像具有空间分辨率高、波段单一的特点。许多卫星同时携带多光谱和全色传感器来同时测量互补图像，如Landsat8、GaoFen2和QuickBird。为了获得高分辨率的多光谱（HRMS）图像，融合LRMS图像和PAN图像的互补信息是一种很有前途的方法。这种技术称为全色锐化(pan-sharpening) 。

全色锐化可以作为典型的图像融合上的超分辨率问题。经典的算法包括分量替换（CS）、多分辨率分析（MRA）等技术。在深度学习时代，卷积神经网络已经成为泛锐化的重要工具。Masi等人提出的泛锐化神经网络（PNN）是开创性的工作之一。借用第一个超分辨率网络的思想，PNN被馈送以PAN图像和上采样LRMS的级联。PNN被馈入PAN图像和上采样LRMS图像的级联，以回归HRMS图像。

实际上，PNN中只有三个卷积单元，所以它是一个相对较浅的网络。近年来，提出了许多模型来改进PNN。由于残差网络的成功，一些论文利用捷径或残差卷积单元来构建深度网络，包括MIPSM、DRPNN和PanNet。它们通常含有10个或更多的卷积单元。除了这些网络之外，为了充分利用神经网络的优点，一些研究人员还建立了更深层次的网络。例如，Wang等人采用密集连接的卷积单元来设计用于全色锐化的44层网络。

众所周知，加深网络的层并不一定能提高性能，因为难以训练更深的网络，并且冗余参数使它们容易过拟合。近年来，遥感界开始重新思考如何充分利用PAN影像的信息。值得注意的是，大多数的全色锐化网络都是把全色图像作为输入的一个通道。这种方式忽略了 PAN和LRMS图像之间的不同特征。越来越多的研究者试图提出双分支网络。在第一阶段，两个分支分别提取PAN和LRMS图像的特征。在第二阶段中，将特征融合以重建HRMS图像。

虽然卷积神经网络在全色锐化方面表现出了良好的性能，但它们需要大量的训练样本，并且它们没有考虑PAN和LRMS图像的观测进程，即：缺乏可解释性。基于模型的深度学习研究是图像处理领域的一个发展趋势，旨在弥补经典模型与神经网络之间差距，并且发现基于模型的深度网络通常优于直观设计的网络。Xie等人提出了一种用于高光谱全色锐化任务的多光谱和高光谱（HS）图像融合网络（MHNet）。毫无疑问，MHNet可以自然地适应全色锐化。尽管如此，MHNet被设计用来描述高光谱图像的低秩特性，我们的实验表明MHNet在全色锐化场景中可能表现不佳。

贡献

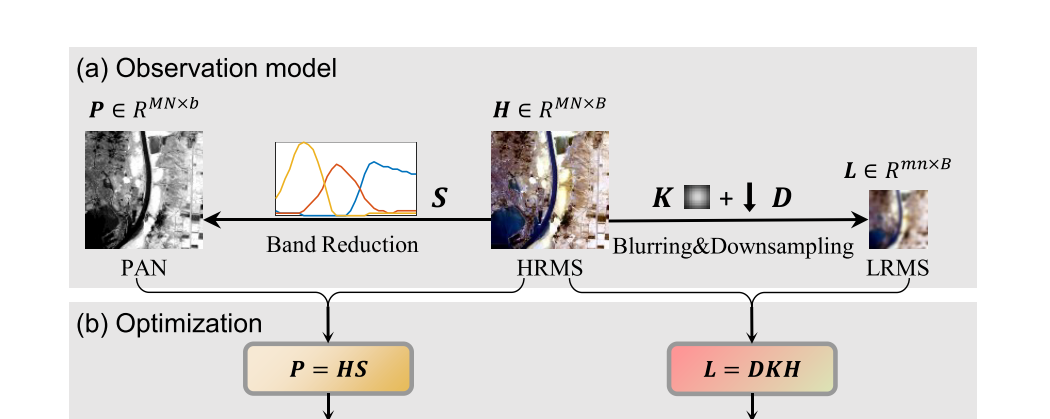
1）本文首先研究了PAN和LRMS图像的生成模型。也就是说，如图1（a）所示，PAN图像是HRMS图像中波段的线性组合，LRMS图像是通过模糊和下采样HRMS图像生成的。结合观测模型和深度先验，我们提出了两个优化问题，它们可以通过图1（b）所示的梯度投影方法得到有效的解决。

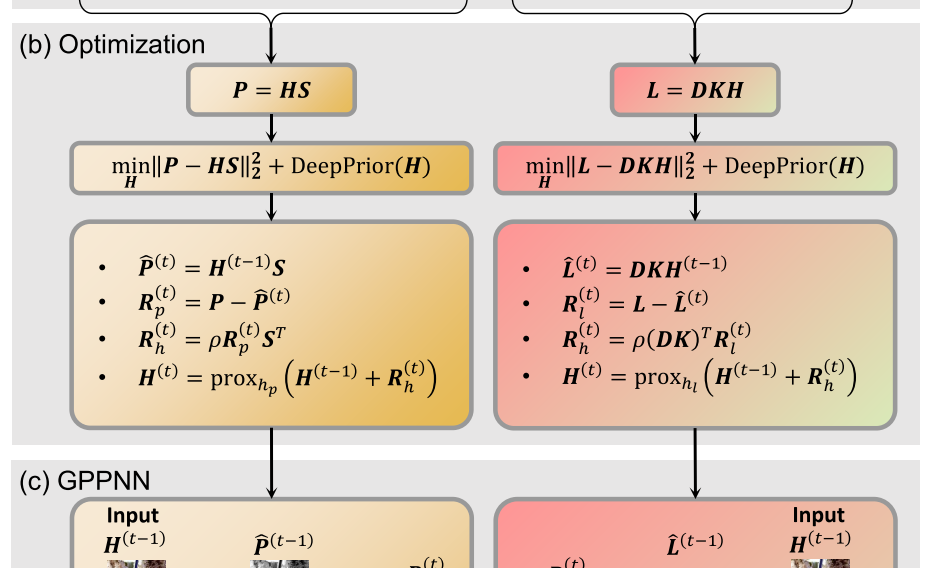
2）受算法展开技术思想的启发，将迭代步骤推广为两个神经块，分别证明了PAN和LRMS图像生成模型的正确性。提出的神经块中的计算流程是可解释的。如图1（c）所示，对于MS Block，给定HRMS图像的当前估计，生成相应的LRMS图像，并计算生成的LRMS图像与真实的图像之间的残差。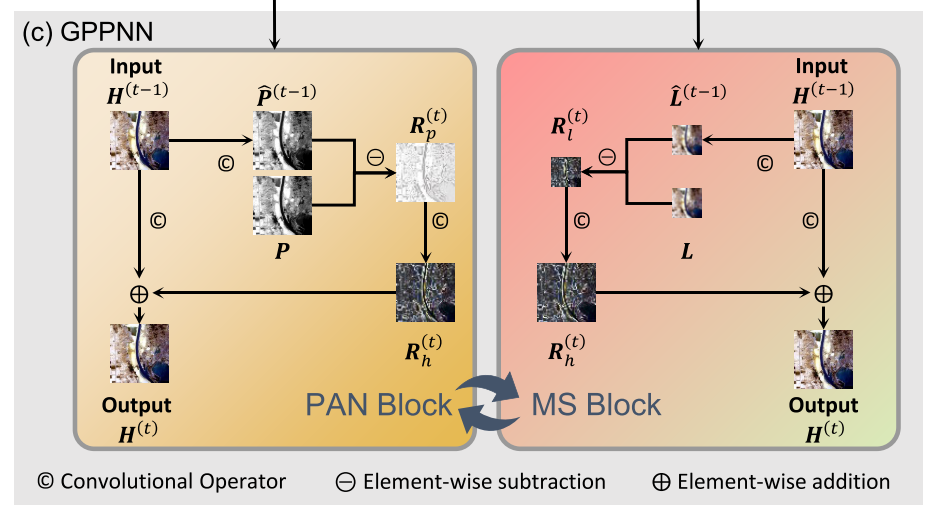
然后，对该残差进行上采样，并将其添加到当前估计中，以重建下一个HRMS图像。PAN嵌段可以类似地解释。我们通过交替堆叠这两个块来构建一个新网络。在下文中，我们称之为基于梯度投影的全色锐化神经网络（GPPNN）。据我们所知，它是第一个用于泛锐化的模型驱动深度网络。

3）将所提出的GPPNN与13种最新的（SOTA）和经典的全色锐化方法进行了比较。在三颗受欢迎的卫星上进行的广泛实验（即，Landsat8、QuickBird、GF2）表明，我们的网络在数量和视觉上都优于其他同类网络。

相关工作

Classic pan-sharpening methods

经典的全色锐化方法主要有基于压缩感知的算法、基于多分辨率分析的算法和其他算法。CS方法假设多光谱图像的空间和光谱信息可以被分解。因此，通过组合PAN图像的空间信息和LRMS图像的光谱信息来重建HRMS图像。在过去的几十年里，研究人员设计了各种分解算法。例如，强度-色调-饱和度（IHS）融合采用IHS变换，Brovey方法使用乘法注入方案，而Gram-Schmidt（GS）方法利用Gram-Schmidt正交化过程。CS方法的主要缺点是如果光谱和空间信息没有被适当地分解，则图像包含伪影。MRA方法将多尺度变换应用于PAN图像以提取空间细节，然后将其注入到上采样的LRMS图像中。典型的算法包括高通滤波器（HPF）融合和感应法、基于平滑滤波器的强度调制（SFIM）。MRA方法的性能强烈依赖于多尺度变换。

Deep learning based methods

近年来，卷积神经网络已成为遥感领域最有效的工具之一。给定一个参数化的网络，它被馈以LRMS图像和PAN图像以回归HRMS图像，并且其参数（或者说，权重）以端到端的方式从数据中学习。第一种尝试是具有三个卷积单元的PNN 。最近，由于计算机视觉的快速发展，它能够训练非常深的网络。研究人员提出了具有几十层的深度全色锐化网络，其性能得到了极大的提高]。同时，研究人员还探索了双分支网络分别从MS和PAN图像中提取特。近年来，泛锐化领域的一个研究趋势是将经典方法与深度神经网络相结合，以提高基于深度学习的方法的可解释性。例如，受MRA算法思想的启发，MIPSM 为PAN图像设计了一个空间细节提取网络，并将细节注入LRMS图像。Liu等人提出了一种自适应权重网络，用于集成不同经典方法的优点。该算法克服了CS和MRA算法的缺点，优于一些基于SOTA的深度学习方法。

Model-driven deep networks

大多数深度神经网络都是凭直觉设计的。最近，越来越多的研究者关注于用于图像处理任务的基于模型的神经网络。模型驱动深度学习的基本思想是通过集成特定任务的先验知识来形成观测模型或优化问题，并将算法步骤的每次迭代转化为一层深度神经网络。通过堆叠的层对应于以一定次数执行算法。基于模型的深度学习搭建了经典模型和深度神经网络之间的桥梁。该思想已经成功地应用于各种任务，包括稀疏编码、压缩感测、图像去模糊、图像去雾和图像去模糊。值得一提的是MHNet，这是一个用于高光谱全色锐化任务的模型驱动网络，可 在MS图像的指导下超分辨HS图像。它可以自然地适用于全色锐化，但是MHNet 主要关注HS图像的低秩属性，即：其秩r_HS远低于B_HS的波段数，实际上一幅HS图像中有几十个甚至几百个波段，而一幅MS图像中的波段数不超过10个。因此，对于MS图像，MHNet的低秩特性不明显，在全色锐化任务中可能会发生故障。

提出的GPPNN方法

在这一节中，我们开发了一个模型驱动的全色锐化网络。为方便起见，在介绍GPPNN之前，我们先对文中的符号进行了总结。L ∈ $R^{mn\times B}$是高为m、宽为n、波段数为B的LRMS图像。H ∈ $R^{MN\times B}$是高M、宽N、波段数B的HRMS图像。P ∈ $R^{MN\times B}$是一幅PAN图像，其空间分辨率与H相同，但只有一个波段（即B =1）。r = M/m = N/n是空间分辨率。在滥用符号的情况下，我们在深度学习的背景下使用它们的张量版本（即L∈ $R^{m\times n\times B}$，H∈ $R^{M\times N\times B}$，P∈ $R^{M\times N\times b}$）。符号转换（·; Cin，Cout）是卷积运算符，其输入和输出分别具有Cin和Cout信道。在下文中，函数Conv（·; cin、cmid、cout）表示级联卷积算子，即，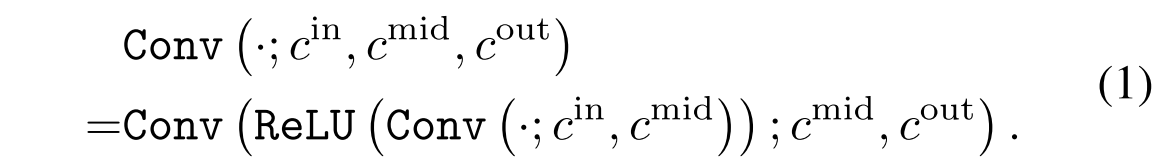

Model formulation

我们的网络从LRMS、HRMS和PAN图像的观察模型开始。假设LRMS图像是通过对HRMS图像进行下采样和模糊而获得的，而PAN图像是HRMS图像的光谱响应的结果。在公式中，我们有L = DKH，P = HS，其中D ∈ $R^{mn\times MN}$表示下采样矩阵，K是（低通）循环卷积矩阵，S ∈ $R^{B\times b}$是所谓的谱响应函数。众所周知，推断HRMS图像是一个不适定问题。因此，它经常公式化以下惩罚优化，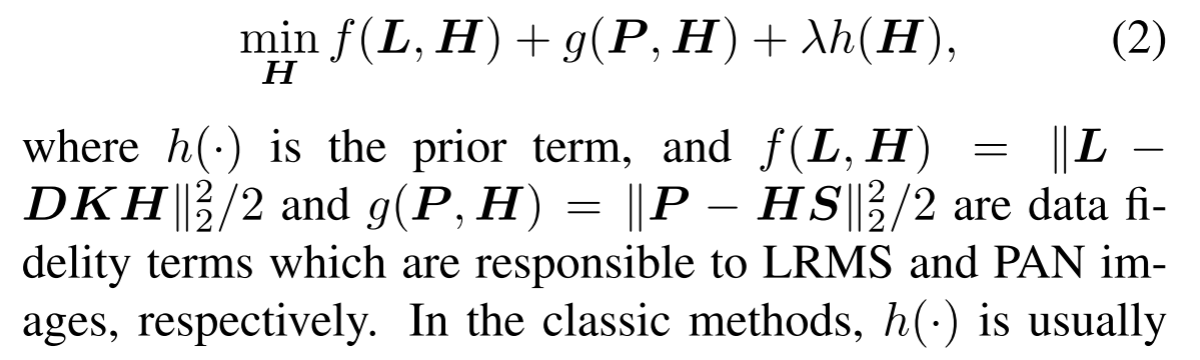
在经典方法中，h（·）通常被设计为手工函数，如总变差或核范数。然而，在深度学习时代，建议将h（·）设置为深度先验。换句话说，最好设置由神经网络参数化捕获的隐式先验。此外，深度先验是从数据中学习的，并且可以适应不同的任务和观察模型。为了充分利用深度先验，我们考虑LRMS感知问题和PAN感知问题，而不是上述问题：

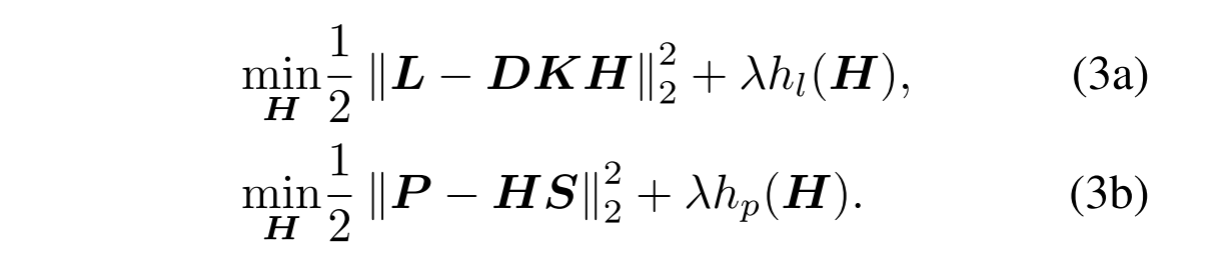
这里，h_l（·）和h_p（·）是分别解释LRMS和PAN图像观测的两个深度先验。

MS Block

我们采用梯度投影法求解Eq.(3a)更新规则为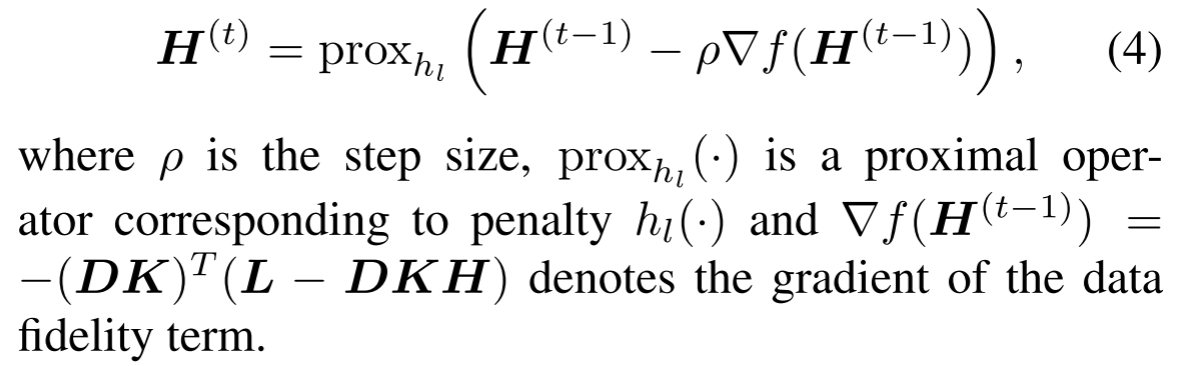
受模型驱动深度学习原理的启发，我们将Eq.(4)作为网络块。开始，Eq.(4)分为如下四个步骤：

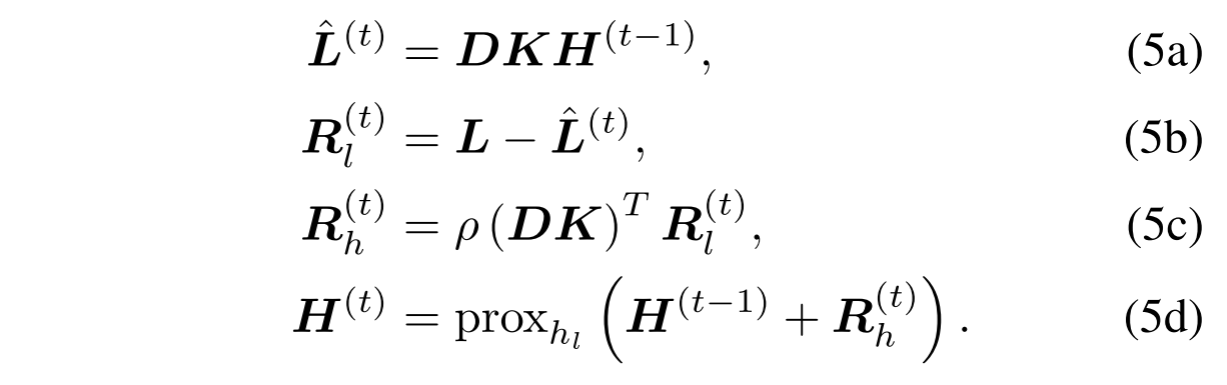
然后，每一步都用深度学习术语来翻译。为了方便起见，我们使用张量版本来表示深度学习环境中的变量。在Eq.(5a)，给定当前HRMS图像$H^{（t-1）}$，它通过应用低通滤波器和下采样生成LRMS图像$L{‘}^{（t）}$。在神经网络中，此步骤通过以下方式实现：

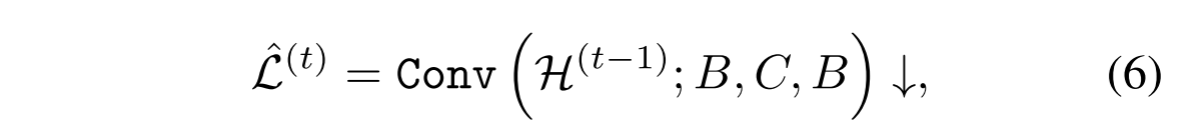
其中下采样用双三次插值↓进行，并且滤波器K由级联卷积算子Conv（·; B、C、B）以获得更有表现力的特征。C是特征图的通道数，本文将其设置为64。B是MS图像的通道数，它取决于输入数据。

之后，Eq.(5b)计算真实LRMS图像L和生成的LRMS图像$L{‘}^{（t）}$之间的残差，并且平移是微不足道的，如以下等式所示，

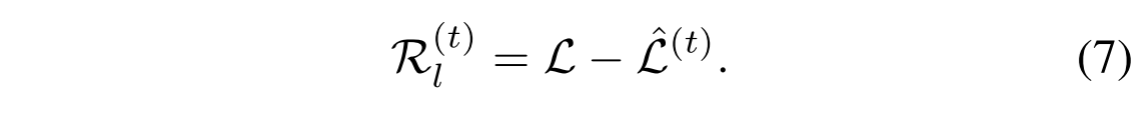
在下一个Eq.(5c)获得高分辨率残差。类似于等式Eqs.(5a)和（6），则该步骤重写为

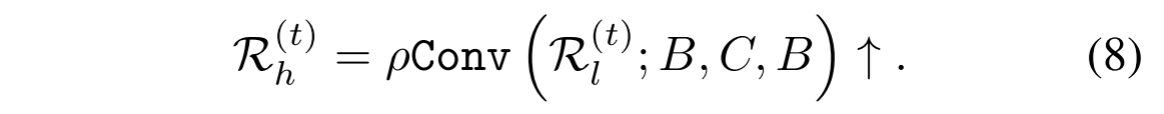
请注意，Eqs.(5a)和（5c）彼此转置，但是我们不强制Eqs.(6)和（8）中的卷积核,满足这种对柔性要求。消融实验表明，它略微改善了GPPNN的性能。最后，方程(5d)通过利用近端算子考虑残差来输出HRMS图像。如前所述，关于深度先验的邻近算子由深度网络建模。以此方式，可以从数据隐式地学习深度先验。所以，我们有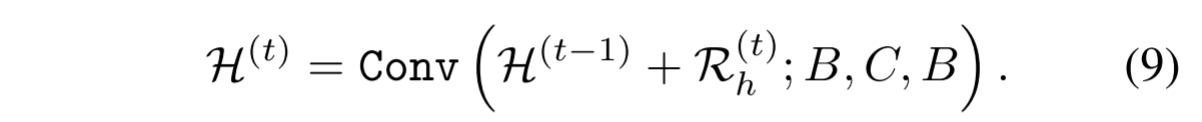

在下文中，Eqs.(6)、（7）、（8）和（9）被命名为MS块。为了更好地理解，MS区块的计算流程如图1（c）所示。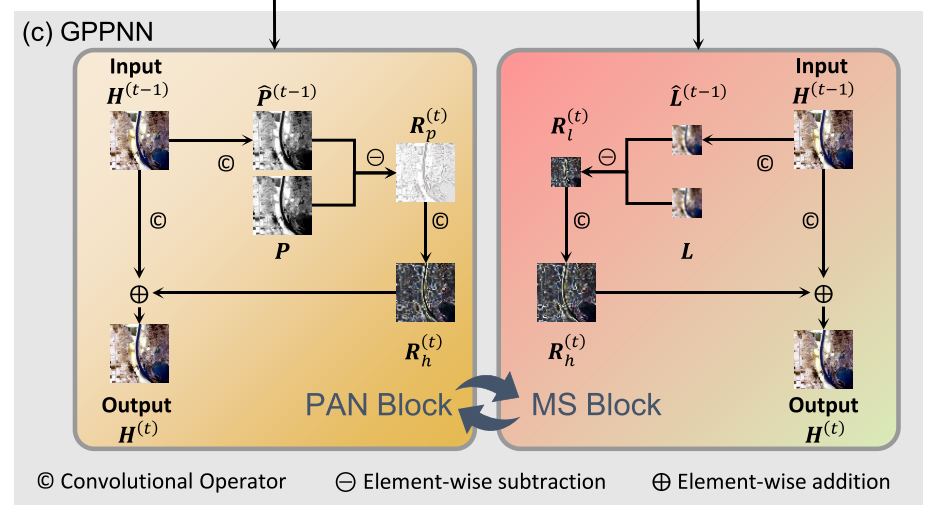

PAN block

在本小节中，我们考虑PAN的观测模型（即：Eq.（3b））。对于梯度投影法，更新规则为

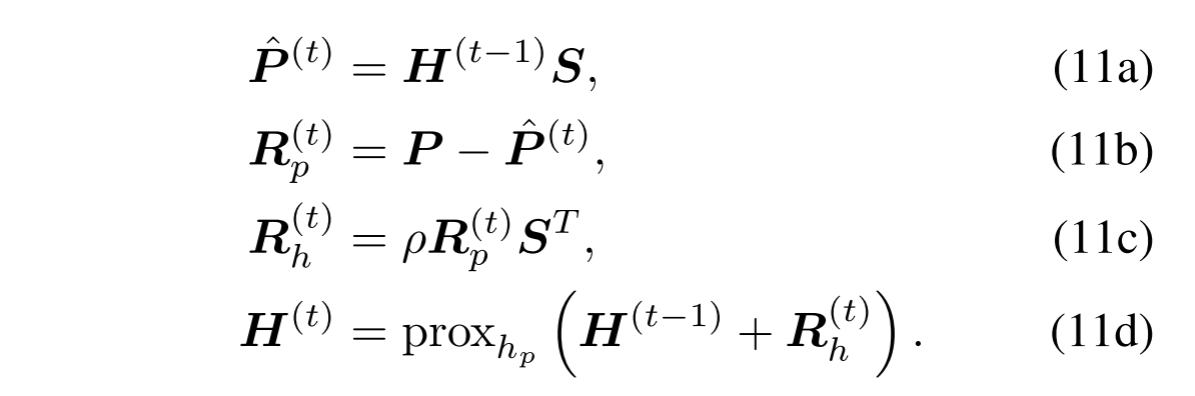
在深度学习的背景下，如图1（c）所示，这些步骤被重写为：

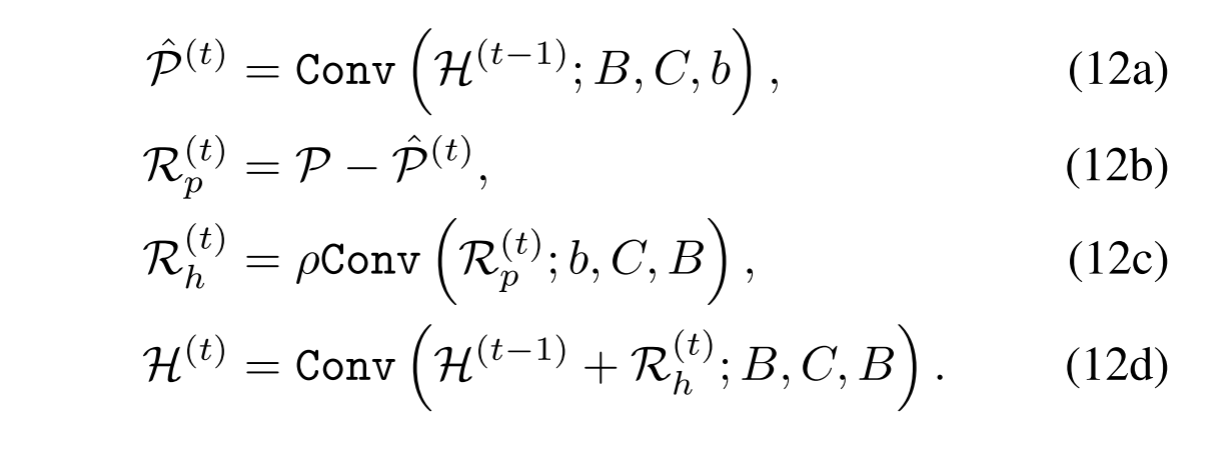
这里，b = 1是PAN图像的通道数。请注意，Eq.(3b)PAN图像是HRMS图像的线性组合。S/$S^T$被认为是一个频带缩减/扩展算子。在此假设下，Eqs.(12a)和（12c）中的每一个都应该具有核大小1。

GPPNN

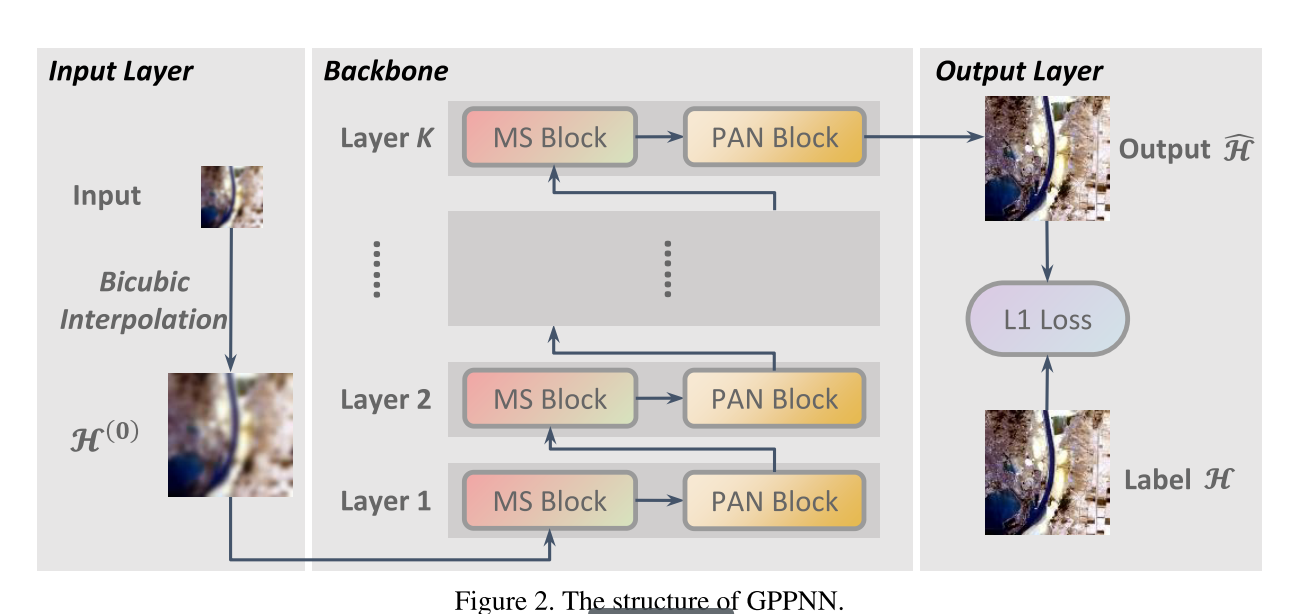
利用MS块和PAN块，我们准备构建基于梯度投影的全色锐化神经网络（GPPNN）。我们的GPPNN的结构如图2所示。网络从输入层开始，需要HRMS图像的初始值。通过对输入的LRMS图像L∈ $R^{m\times n\times B}$进行双三次插值来初始化$H^{（0）}$∈ $R^{M\times N\times B}$。网络后面是主干子网。有K层，每层由MS块和PAN块组成。公式中有