————————————————————————————————

查询数据的时间复杂度

首先，数组查询数据的时间复杂度是O(n)——>如何降低查询的时间复杂度?
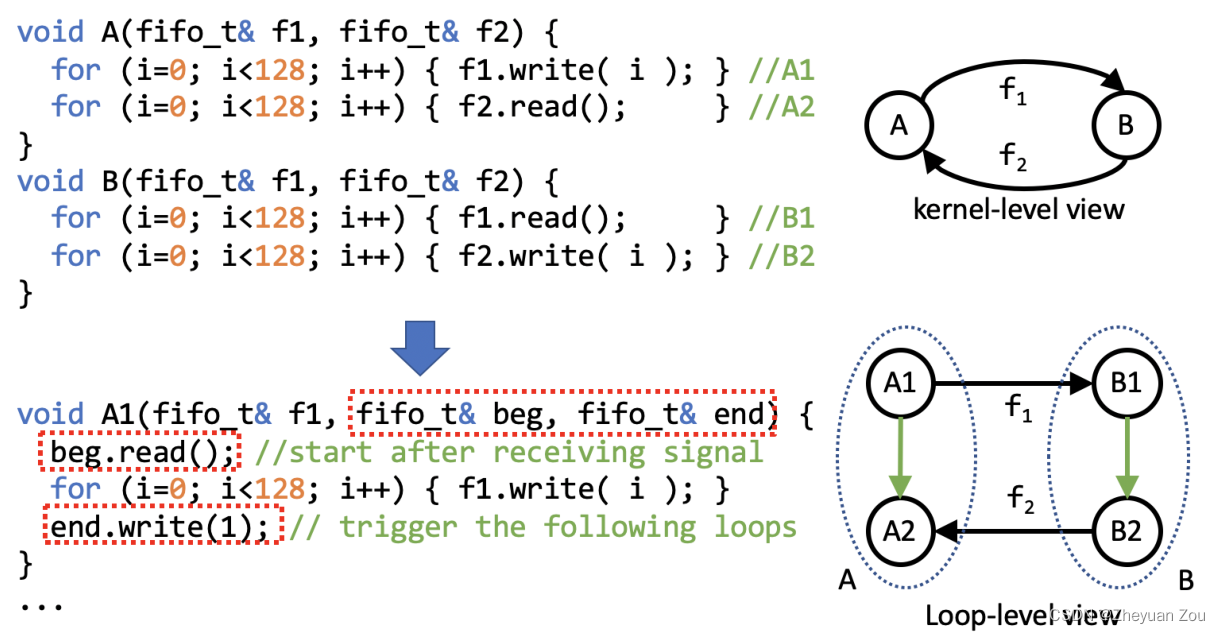
—1—>二分法： 时间复杂度O(logn)—>要使用二分法，数据必须有序—>排序的时间复杂度O(n)—>因此，总的时间复杂度O(nlogn)

—2—>哈希表： 根据一个式子（如：n%arr.length）计算数据要放入的地址—>要查找某一个数时，直接根据数据找下标查询—>时间复杂度O(1)
哈希表缺点：
1）用户存储数据往往是无序的，因此存储数据时有风险，后来插入的数据可能会覆盖原来的数据
2）二维数组可以防覆盖，但是数组的大小在创建的时候已经固定，因此同一列插入的数据有限，虽然可以进行数组的扩容，但是会出现大量空间闲置的情况，是对内存区域极大的浪费

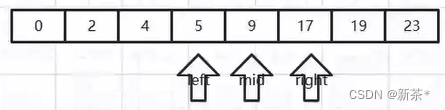
—3—>链表： 解决多个数据计算得到的位置相同的情况
链表缺点：
1）链表如果过长，查询的时候时间复杂度是O(n)，没有起到降低时间复杂度的效果
2）当·链表长度过长的时候，需要把链表变成一棵树

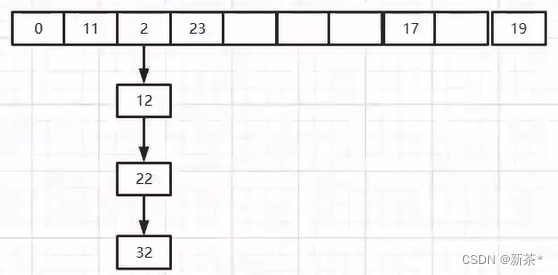
—4—>有序二叉树：
1）对于这棵有序二叉树，查询的时间复杂度为O(logn)
例如：如果要查询6，6和10比较，6比10小，则右边的树肯定比6大、可以放弃查找，因此向左查找（这样相当于省去了查找一半的数据）；6再和5比较，6比5大，则向右查找，放弃5左边的数据；
从上述过程可知，每次查找都相当于放弃了一半的数据，因此查询的时间复杂度为O(logn)

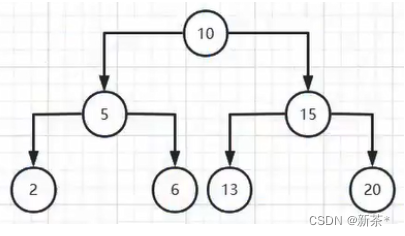
2）但是并不是所有有序二叉树的查询时间复杂度都是O(logn)
有序二叉树特点：左子树节点小于父节点，右子树节点大于父节点
例如：将下列数组构建成有序二叉树可得

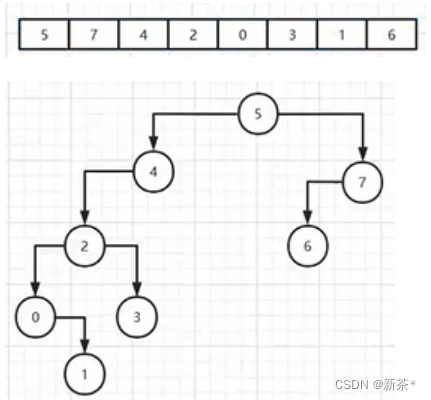
由此可知，有序二叉树的查询时间复杂度并不严格为O(logn)，而是在O(logn)和O(n)之间，所以有序二叉树的查询不稳定
如何让查询时间复杂度变稳定？？——>平衡二叉树
—5—>平衡二叉树：
平衡二叉树是在有序二叉树的基础之上得来的

平衡二叉树

平衡二叉树特点：一个节点的左右子树的高度差的绝对值不超过1

旋转策略

如果插入的数据使某一结点左右子树的高度差超过了1，那么就造成了不平衡，——>通过LL、RR、LR、RL四种旋转策略保证树的平衡

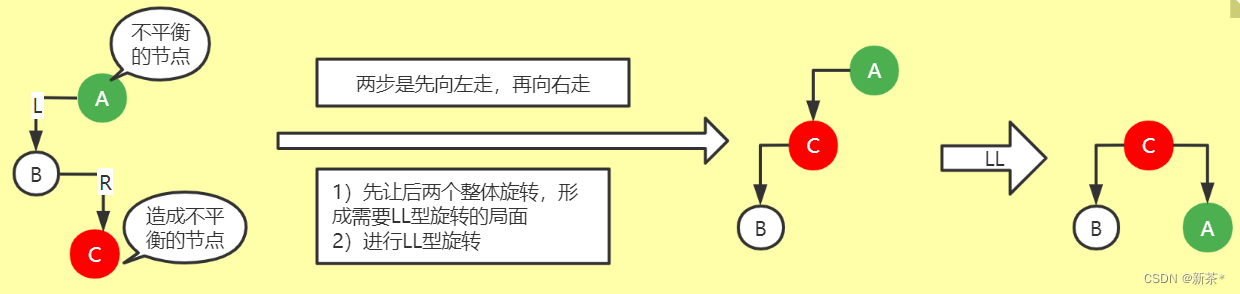
假设：插入的节点为造成不平衡的节点（红色C），当前不平衡的节点（绿色A）

方法：从当前不平衡的节点（绿色A）向造成不平衡的节点（红色C）走两步

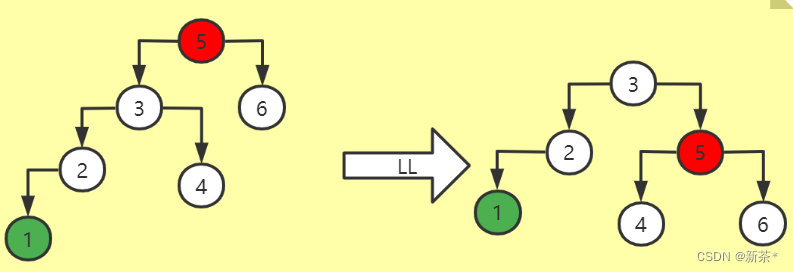
1、LL型旋转：

两步都是向左走，则为LL型旋转
1）将A的左子树升为新的根节点；
2）将原来的根节点A降为B的右子树；
3）各个子树（C）按大小关系进行排序（相当于子树重新构建一遍）。

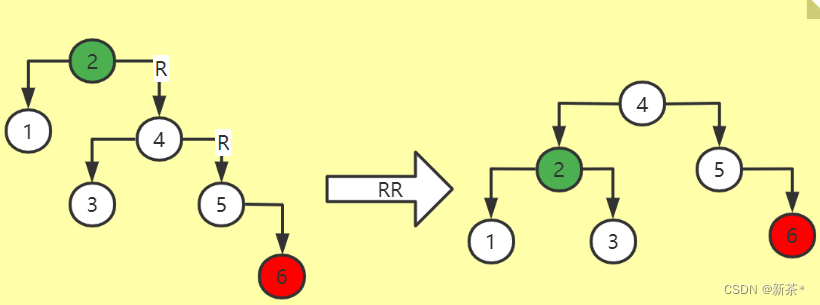
2、RR型旋转：

两步都是向右走，则为RR型旋转
1）将A的右子树升为新的根节点；
2）将原来的根节点A降为B的左子树；
3）各个子树（C）按大小关系进行排序（相当于子树重新构建一遍）。

3、LR型旋转：

两步是先向左走，再向右走
1）先让后两个整体旋转，形成需要LL型旋转的局面
2）再进行LL型旋转

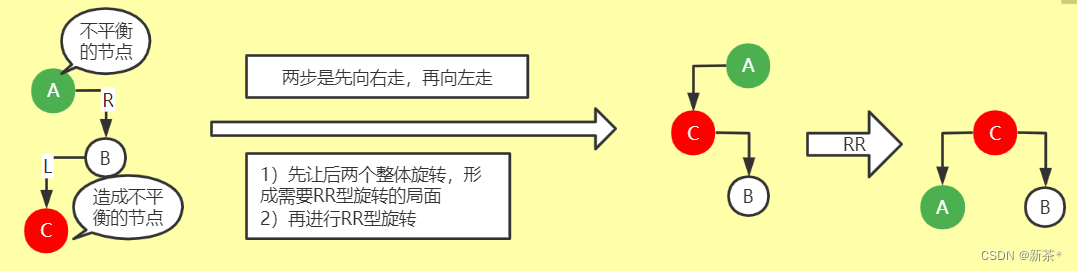
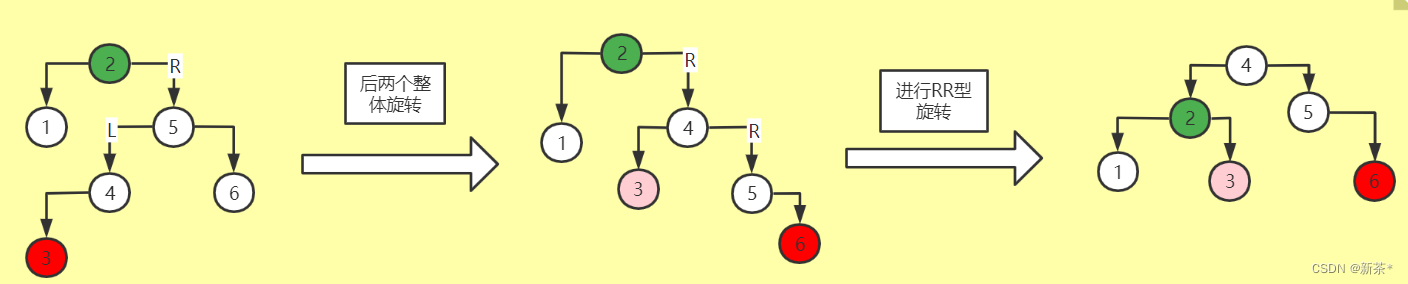
4、RL型旋转：

两步是先向右走，再向左走
1）先让后两个整体旋转，形成需要RR型旋转的局面
2）再进行RR型旋转

补充：

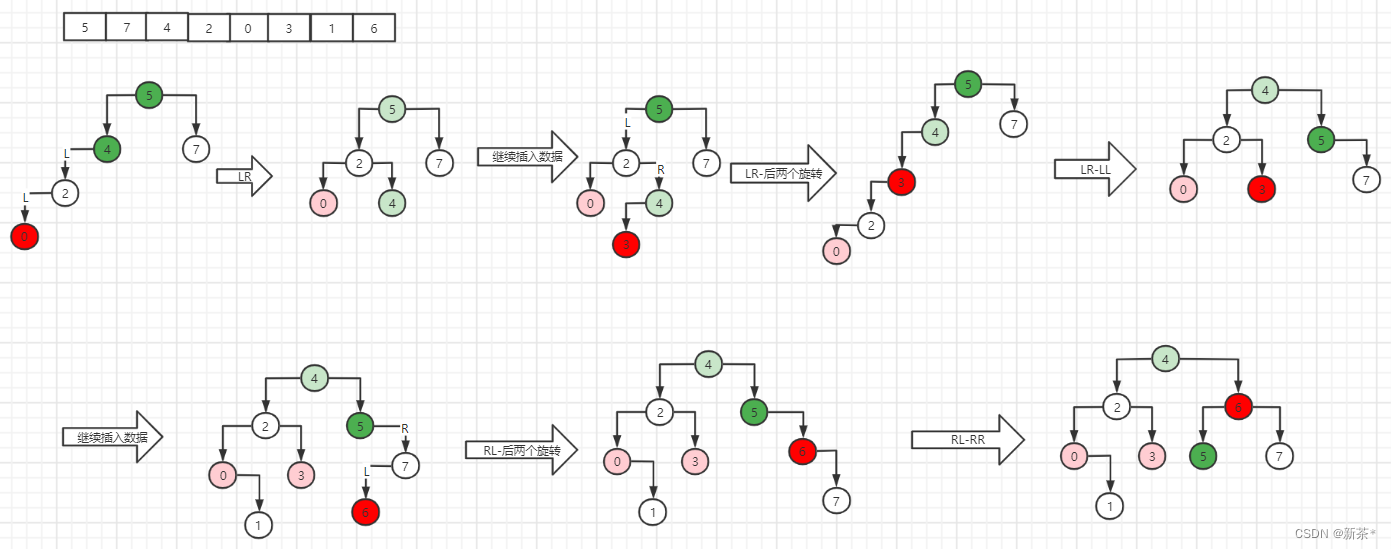
1）如果树中不止一个节点不平衡，选择离造成不平衡节点（红色）最近的节点；
2）将数组转化成平衡二叉树时，插入某一个节点后造成不平衡，则先将树旋转平衡后再插入后面的数据；