一、异常检测的概率模型

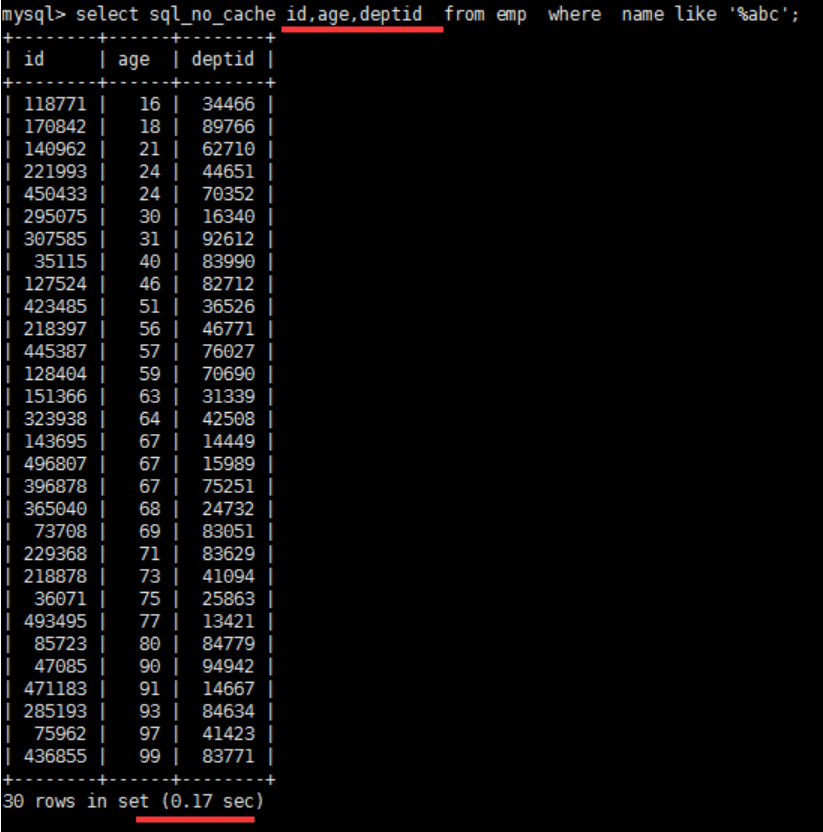
        为您的数据选择合适的模型，选择一个概率阈值，低于该阈值将数据标记为异常，计算观察数据中每个实例的概率，低于阈值的情况属于异常情况。

        研究表明，世界杯比赛的进球数可以很好地近似于泊松分布。在一场比赛中进n球的概率由下式给出：

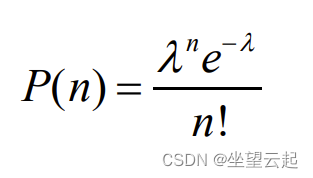
，其中λ是每场比赛的平均进球数。

         对于现代世界杯赛事，λ=2.5，使用下面的概率表，我们看到有7或8个进球的比赛将被标记为异常[P（n）<2%]，但是发现异常并不意味着打假球，但是有7个进球的比赛仍然有可能是偶然发生的。

         异常检测概率模型本身的问题：模型不合适、参数错误、测试统计数据选择不当。

二、极值分析

        有时，反常现象是一种极端事件：非常大的保险损失、非常大的洪水、非常炎热的夏天等等。由于此类事件可能是灾难性的，因此很自然地会问这些极端事件的可能性有多大。问题在于极端事件很少发生，因此很难用典型的概率分布进行建模，因为可用数据很少。

1、GEV分布

        考虑一系列独立分布的随机变量，示例：Xi是第i天的每日臭