概率论：方差、标准差、协方差、皮尔逊相关系数、线性相关

news2024/11/28 21:48:24

方差和标准差：

一个随机变量 $\textup{x}$ ， $\textup{x}$ 的值的变化程度可以用方差计算：

$\textup{Var}(\textup{x})=\textup{E}[(x-E[\textup{x}])^{2}]$ ；其中 $E[\textup{x}]$ 是期望。

我们举个例子：

$\textup{x}$ 服从均一分布， $\textup{x}$ 取值为0.1，0.2，0.3，0.4，0.5 ，每种值的概率是20%，可算出期望是0.3，那么方差就是：

$\textup{Var}(\textup{x})=\textup{E}[(x-E[\textup{x}])^{2}]\\ =0.2*(0.1-0.3)^{2}+0.2*(0.2-0.3)^{2}+0.2*(0.3-0.3)^{2}+0.2*(0.4-0.3)^{2}+0.2*(0.5-0.3)^{2}\\ =0.2*0.1$

标准差是方差的平方根，随机变量 $\textup{x}$ 的标准差是 $\sqrt{0.2*0.1}$

协方差：

协方差可以用来衡量两个变量的线性相关性，并且可以化简到容易计算的形式（化简过程有问题可以找下证明或者举个例子亲自算一下）：

$\textup{Cov}(\textup{x,y})=\textup{E}[(x-E[\textup{x}])(y-E[\textup{y}])]\\ \\=\textup{E}[\textup{xy}]-2\textup{E}[\textup{x}]\textup{E}[\textup{y}]+\textup{E}[\textup{x}]\textup{E}[\textup{y}]\\\\ =\textup{E}[\textup{xy}]-\textup{E}[\textup{x}]\textup{E}[\textup{y}]$

我们举第一个例子：

$\textup{x}$ 服从均一分布， $\textup{x}$ 取值为0.1，0.2，0.3，0.4，0.5 ，每种值的概率是20%，可算出期望是0.3，标准差是 $\sqrt{0.2*0.1}$ ；

$\textup{y}$ 服从均一分布， $\textup{y}$ 取值为10000，20000，30000，40000，50000 ，每种值的概率是20%，可算出期望是30000，标准差是 $\sqrt{0.2*1000000000}$ ；

假设 $\textup{x}$ 和 $\textup{y}$ 线性相关，此时 $\textup{y}=100000\textup{x}$ ，那么 $\textup{x}$ 取0.1 $\textup{y}$ 取10000的概率为0.2， $\textup{x}$ 取0.1 $\textup{y}$ 取20000、30000、40000、50000的概率都为0，以此类推。

$\textup{x}$ 和 $\textup{y}$ 的协方差就是：

$\textup{Cov}(\textup{x,y})=\textup{E}[\textup{xy}]-\textup{E}[\textup{x}]\textup{E}[\textup{y}]\\ =0.2*(0.1*10000)+0.2*(0.2*20000)+0.2*(0.3*30000)+0.2*(0.4*40000)+0.2*(0.5*50000)-0.3*30000\\ =0.2*55000-0.3*30000\\ =2000$

我们再举第二个例子：

把上个例子中的随机变量 $\textup{y}$ 改变，随机变量 $\textup{x}$ 不改变。

$\textup{y}$ 服从均一分布， $\textup{x}$ 取值为1，2，3，4，5 ，每种值的概率是20%，可算出期望是3，标准差是 $\sqrt{0.2*10}$ ；

假设 $\textup{x}$ 和 $\textup{y}$ 线性相关，此时 $\textup{y}=10\textup{x}$ ，那么 $\textup{x}$ 取0.1 $\textup{y}$ 取1的概率为0.2， $\textup{x}$ 取0.1 $\textup{y}$ 取2、3、4、5的概率都为0，以此类推。

$\textup{x}$ 和 $\textup{y}$ 的协方差就是：

$\textup{Cov}(\textup{x,y})=\textup{E}[\textup{xy}]-\textup{E}[\textup{x}]\textup{E}[\textup{y}]\\ =0.2*(0.1*1)+0.2*(0.2*2)+0.2*(0.3*3)+0.2*(0.4*4)+0.2*(0.5*5)-0.3*3\ =0.2*5.5-0.3*3\\ =0.2$

两个例子对比一下，两个例子中的两个随机变量都是线性相关的，求出来的协方差都大于0，但是两个协方差的数值有较大差异，相差了10000倍。

皮尔逊相关系数：

皮尔逊相关系数是两个随机变量 $\textup{x}$ 和 $\textup{y}$ 的协方差与标准差之商：

$\rho _{\textup{x}\textup{y}}=\frac{Cov(\textup{x,y})}{\sigma \textup{x}\sigma \textup{y}}$

我们可以计算上述两个例子里的皮尔逊相关系数：

第一个例子：

$\rho _{\textup{x}\textup{y}}=\frac{Cov(\textup{x,y})}{\sigma \textup{x}\sigma \textup{y}}\\ \\=\frac{2000}{\sqrt{0.2*0.1}\sqrt{0.2*1000000000}}\\ \\=\frac{2000}{2000}=1$

第二个例子：

$\rho _{\textup{x}\textup{y}}=\frac{Cov(\textup{x,y})}{\sigma \textup{x}\sigma \textup{y}}\\ \\=\frac{0.2}{\sqrt{0.2*0.1}\sqrt{0.2*10}}\\ \\=\frac{0.2}{0.2}=1$

皮尔逊相关系数都为1。

协方差、皮尔逊相关系数与线性相关

完全线性相关、线性相关、线性独立、完全独立：

如果变量 $\textup{y}$ 可以用 $\textup{x}$ 表示成 $\textup{y=ax+b}$ ，那么两个随机变量完全线性相关，否则不是完全线性相关。不是完全线性相关的两个变量有可能线性相关，有可能线性独立。如果两个变量有一定的线性关系，那么两个变量线性相关；如果 $\textup{x}$ 和 $\textup{y}$ 没有任何关系（完全独立）或者左右对称的线性关系可以抵消掉，那么两个变量线性独立。我们举一些例子。

完全线性相关的例子：

如果 $\textup{y=2x+1}$ ，点集如散点图所示，那么概率矩阵和计算协方差如下，协方差为4大于0（绿色部分值的加和），皮尔逊系数为1：

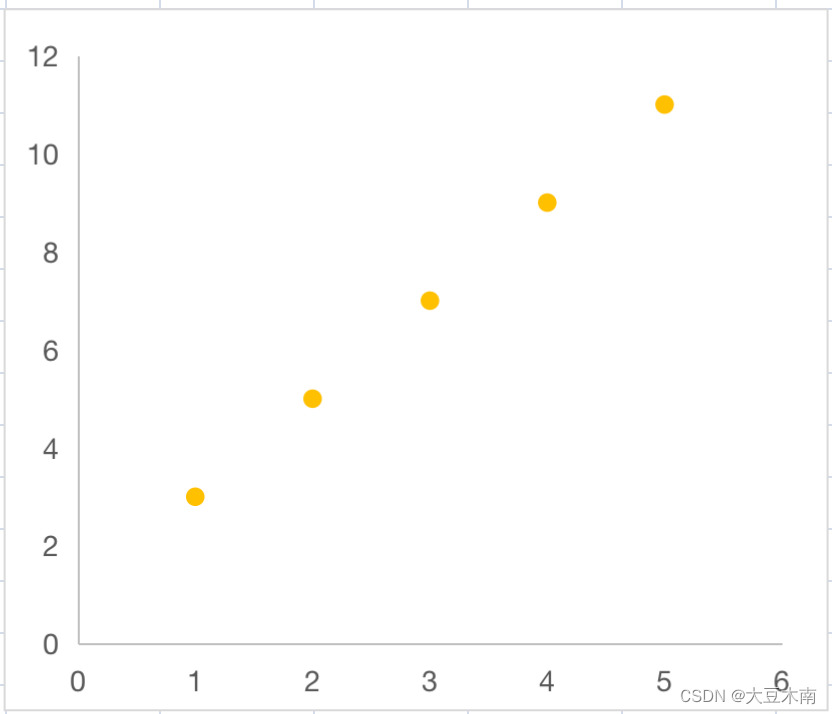
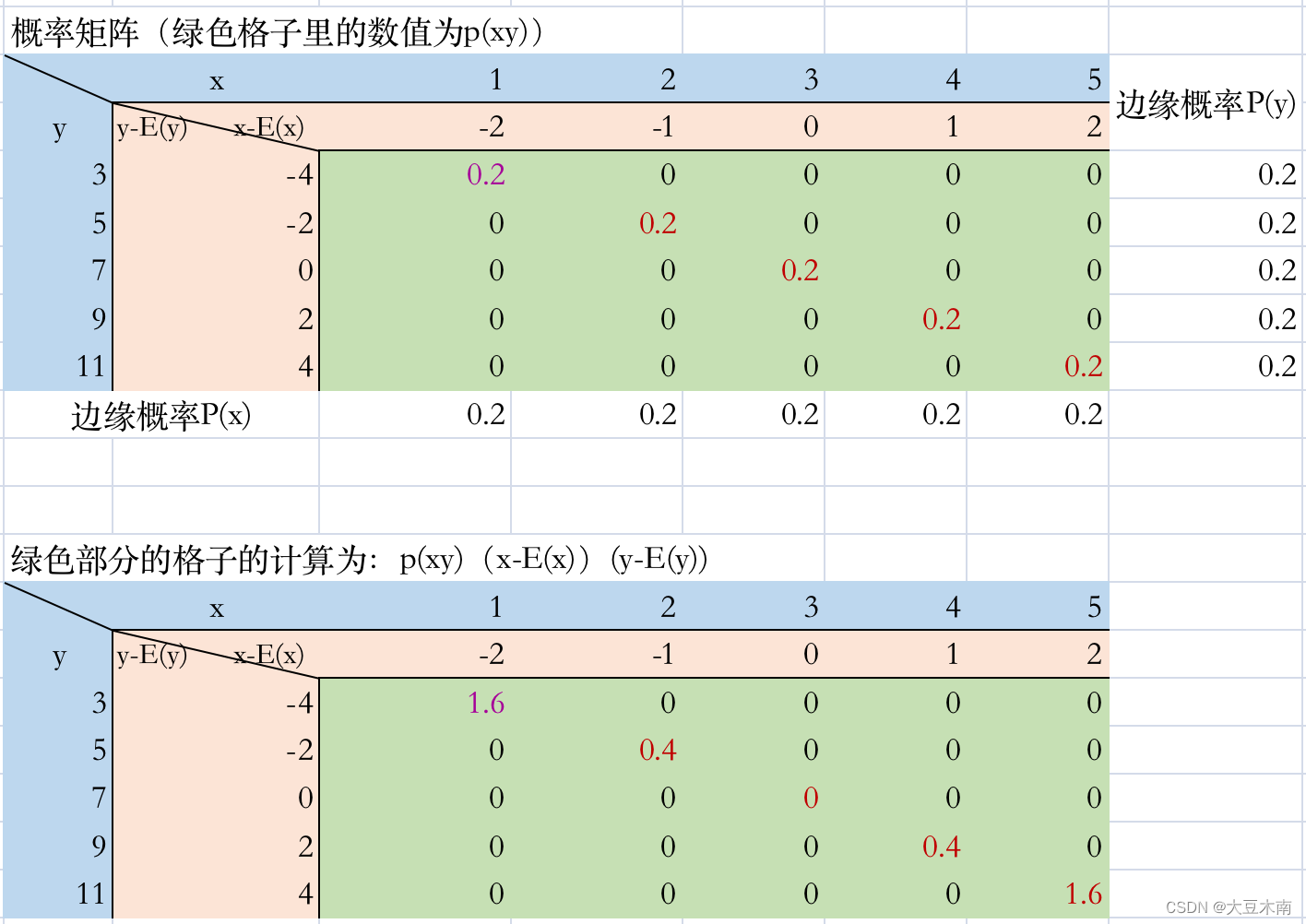
线性相关的例子：

如果 $\textup{y=x}^{2}$ ，点集如散点图所示，那么概率矩阵和计算协方差如下，协方差为12大于0，皮尔逊系数为0.98：

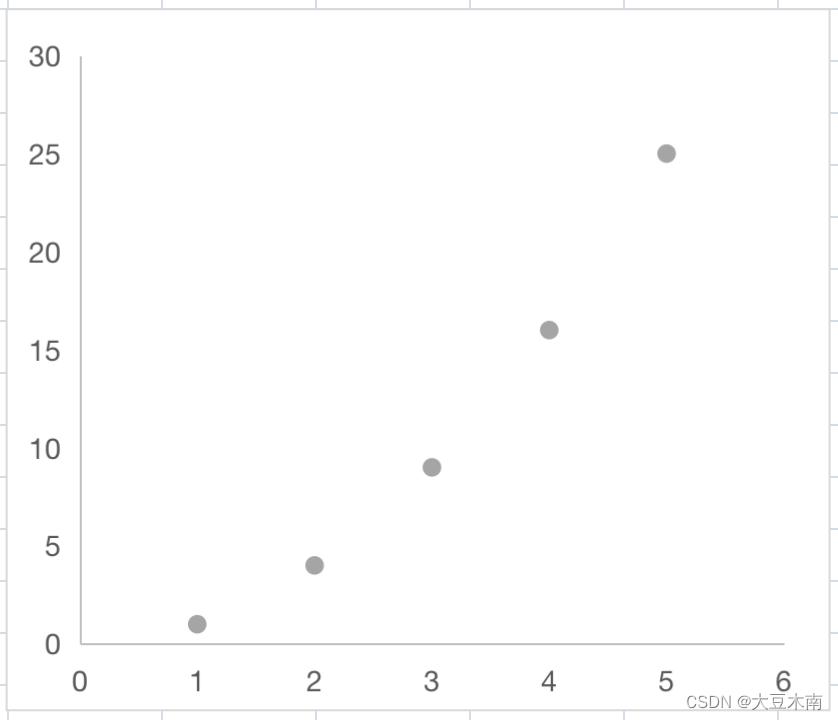
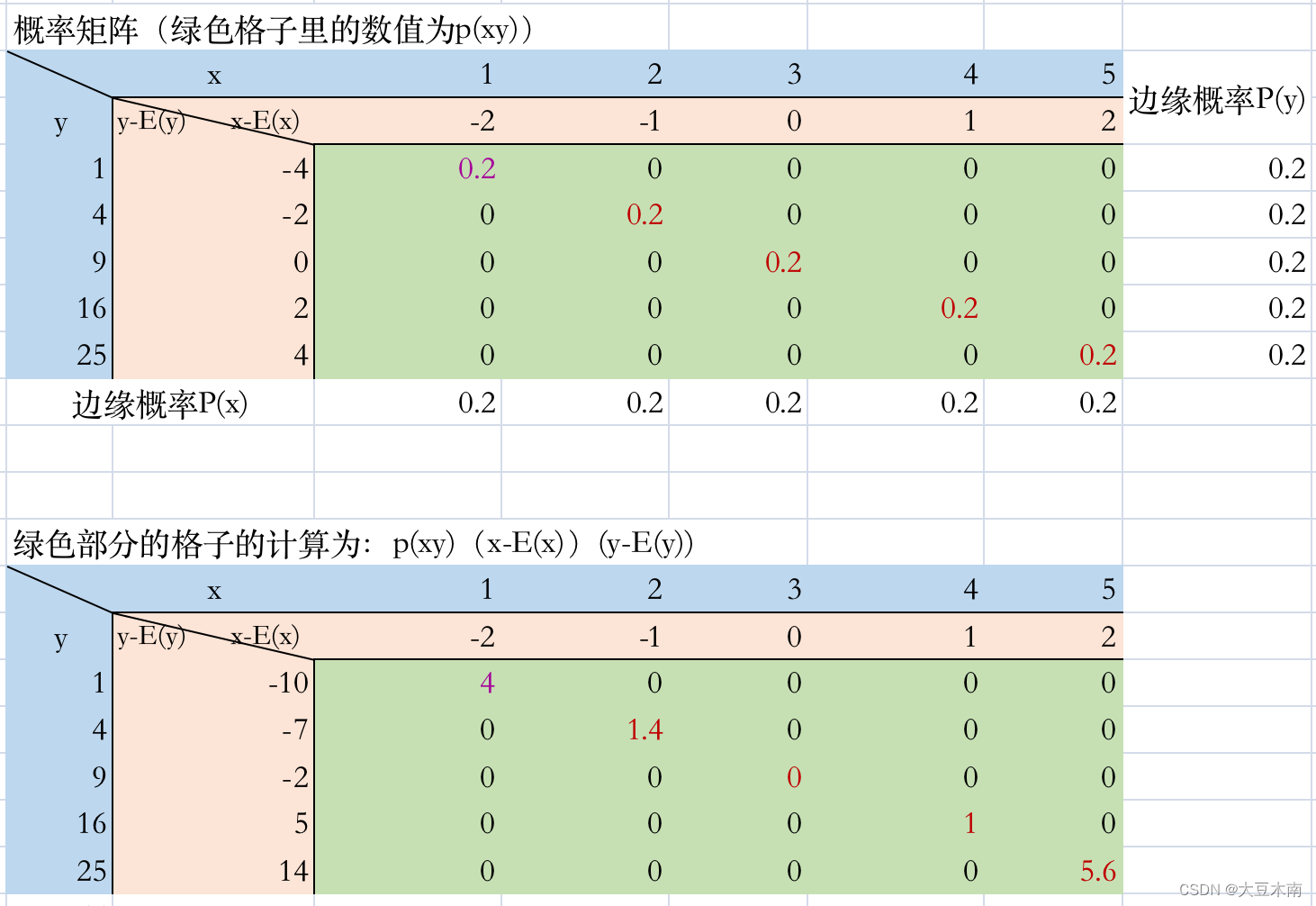
线性独立的例子：

仍然是 $\textup{y=x}^{2}$ ，取不同的数值再算一下，点集如散点图所示，协方差为0，皮尔逊系数为0，此时左右对称的线性关系可以抵消掉：

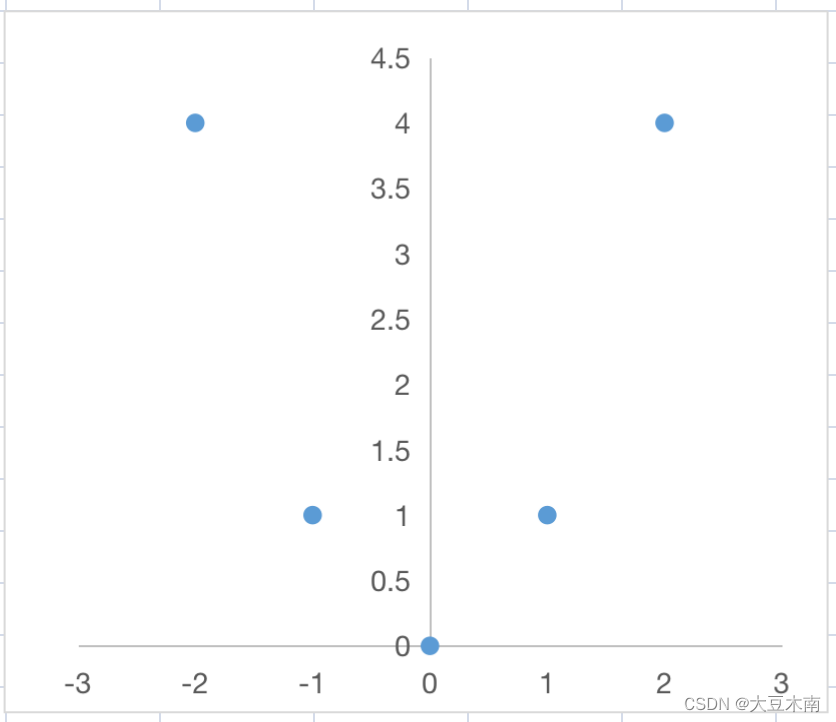
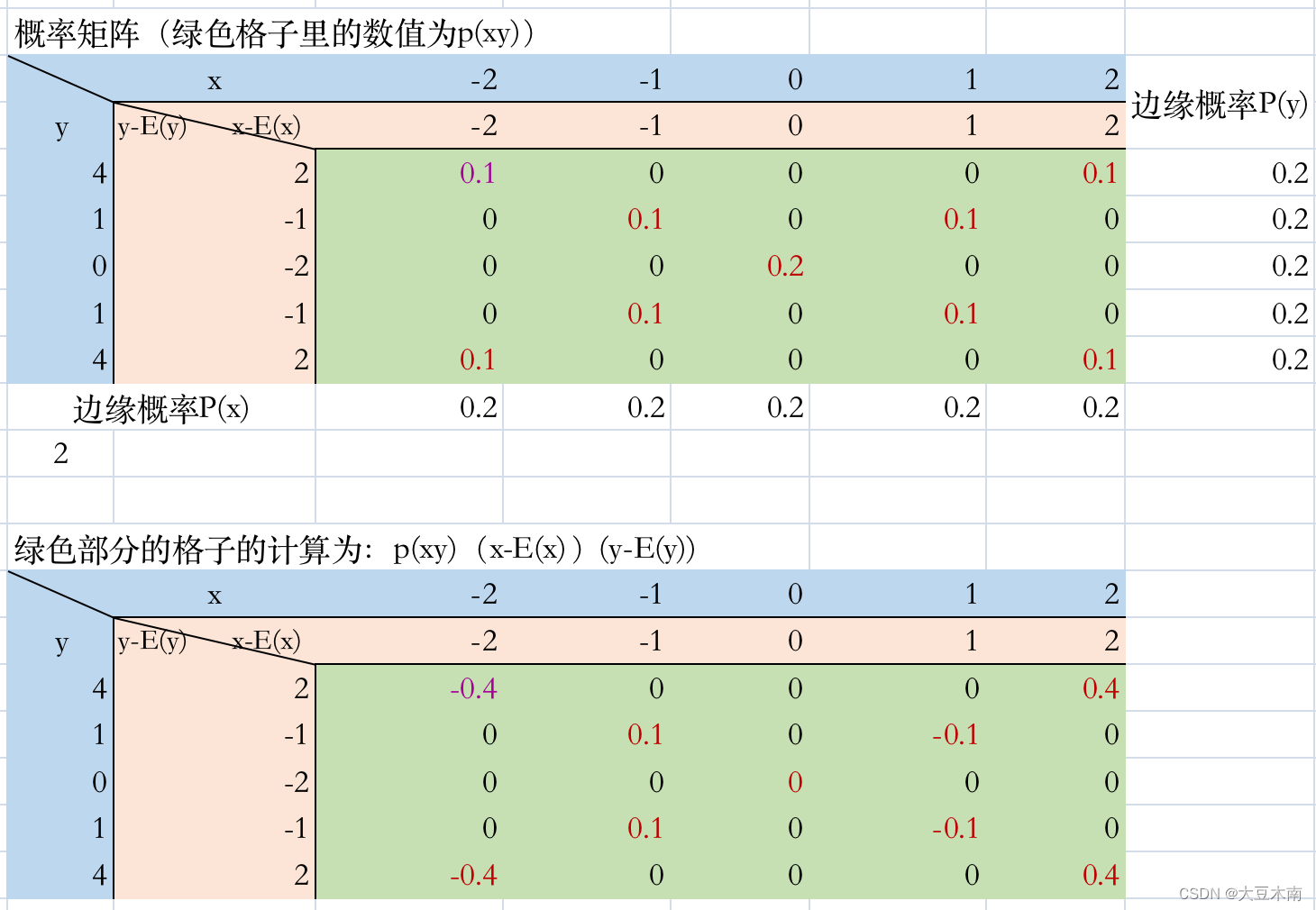
线性独立的另外一个例子，点集如散点图所示，此时 $\textup{x}$ 和 $\textup{y}$ 完全独立，协方差为0，皮尔逊系数为0：

通过上述例子可以看出，当两变量线性独立时，协方差一定等于0；当协方差等于0时，两变量也一定线性独立，但是并不代表两变量完全独立（完全独立的例子）。

下图是皮尔逊相关系数的一个图示便于理解：

总结

如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

协方差和皮尔逊相关系数都可以衡量两个随机变量的线性相关性（注意只是线性相关性），协方差受随机变量数值大小的影响，而皮尔逊相关系数不受随机变量数值大小的影响。所以两随机变量的协方差越大并不代表这两个变量越线性相关，而两随机变量的皮尔逊相关系数绝对值越大这两个变量越线性相关。

协方差的范围是 $[-\infty ,\infty ]$ ；协方差<0时，线性负相关；协方差>0时，线性正相关；协方差=0时，线性独立。皮尔逊相关系数的范围是 $[-1,1]$ ；当为-1时，完全线性负相关；当为1时，完全线性正相关；当>-1且<0时，线性负相关，绝对值越大越线性负相关；当>0且<1时，线性正相关，绝对值越大越线性正相关；当=0时，线性独立。