冈萨雷斯DIP第7章知识点

news2024/11/29 22:52:06

文章目录

- 7.3 相关
- 7.5 基图像
- 7.6 傅里叶相关变换
- - 7.6.1 离散哈特利变换
  - 7.6.3 离散正弦变换

DIP的其他章节都好复习，唯独就这个第7章小波变换。复习起来十分头大，所以我开始写他的课后题，雾。

7.3 相关

已知两个连续函数 $f (x)$ 和 $g (x)$ ， $f$ 和 $g$ 的相关(当 $f (x) \neq = g (x)$ 时，称为互相关；当 $f (x) = g (x)$ 时，称为自相关)定义为

$\star g(\Delta x)=\int_{-\infty}^{\infty} f^{*}(x) g(x+\Delta x) \mathrm{d} x=\langle f(x), g(x+\Delta x)\rangle$

相关有时称为 $f$ 和 $g$ 的滑动内积，度量的是 $f (x)$ 和 $g (x)$ 的相似性，是它们相对位移 $Δ x$ 的函数。若 $Δ x = 0$ ，则有

$\star g(0)=\langle f(x), g(x)\rangle$

基函数 $h$ 的能量，在时间-频率平面上集中于点 $μ_t, μ_f)$ 处。大部分能量，落在面积为 $4σ_tσ_f$ 的一个矩形区域(称为海森堡盒或单元)，

$\sigma_{t}^{2} \sigma_{f}^{2} \geq \frac{1}{16 \pi^{2}}$

因为函数的支撑集定义为函数非零的点的集合，由海森堡测不准原理知，函数在时间和频率上都存在有限支撑集是不可能的。

7.5 基图像

注意：最大频率的DFT、DHT 基图像，出现在 $u = 4$ 和 $v = 4$ 时。离散余弦变换、离散正弦变换出现在 $u = 7, v = 7$ 时。

7.6 傅里叶相关变换

7.6.1 离散哈特利变换

$u)=\frac{1}{\sqrt{N}} \operatorname{cas} \frac{2 \pi u x}{N}=\frac{1}{\sqrt{N}}\left(\cos \frac{2 \pi u x}{N}+\sin \frac{2 \pi u x}{N}\right)$

7.6.3 离散正弦变换

类似于DCT，DST具有与DFT大致相同的频率范围，但频率分辨率是后者的2倍。注意：与DCT和DFT的不同之处，DST没有直流(u=0)分量。

$u)=\sqrt{\frac{2}{N+1}} \sin \frac{(x+1)(u+1) \pi}{N+1}$

close all; clear all; clc;
A = dctmtx(8);
B = A';
C = zeros(8, 8, 64);
m = 0;
for i = 1:8
    for j = 1:8
        m = m+1;
        C(:, :, m) = B(:, i)*A(j, :);
    end
end
minvalue = min(min(min(C)));
maxvalue = max(max(max(C)));
figure,
%显示灰度图像的范围，指定为 [low high] 形式的二元素向量。
% imshow 函数将值 low（以及任何小于 low 的值）显示为黑色，并将值 high（以及任何大于 high 的值）显示为白色。
for k = 1:64
    subplot(8, 8, k), imshow(C(:, :, k), [minvalue, maxvalue]);
end

在这里插入图片描述
对于长度为 $N=2^J$ 的输入序列， FWT： $O (N)$ ； FFT： $O(N\log_2N)$ 。

为更好地控制时间-频率平面的划分(即得到更小的高频带宽)，必须将 FWT 推广到称为小波包的更灵活的分解。这一推广的代价是，计算复杂度：从FWT的 $O (N)$ 增加到小波包的 $O(N\log_2N)$ ，与FFT相同。

7.35 推导公式(7.140)

$d_{j}(k)=\sum_{n} h_{\psi}(n-2 k) c_{j+1}(n)\tag{7.140}$

这个公式是快速小波变换中的，大概的含义就是小波空间 $W_j$ 中的函数可以由尺度空间 $V_{j+1}$ 中的函数来表示。这个是方便理解的，我们可以看书上的这张图。

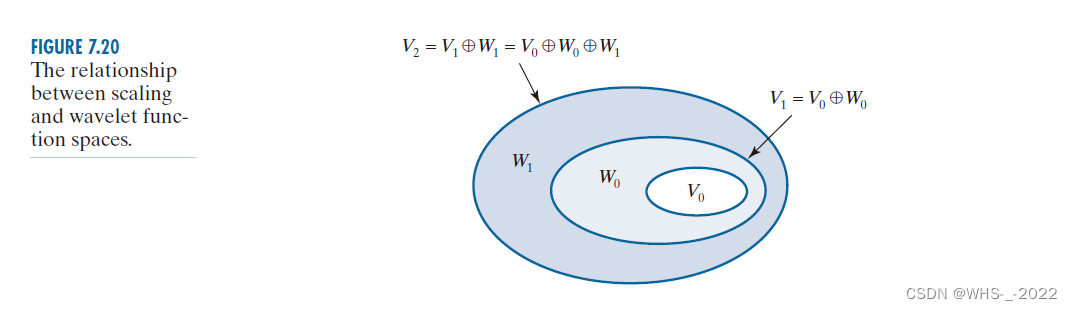
在这里插入图片描述
根据式(7.135)
$d_{j}=\left\langle f(x), \psi_{j, k}(x)\right\rangle\tag{7.135}$

我们可以得到：

$d_{j}(k)=\int f(x) 2^{j / 2} \psi\left(2^{j} x-k\right) d x$

但是这里我们要推导的是细节系数和尺度系数之间的关系，所以需要将 $\psi\left(2^{j} x-k\right)$ 替换掉。我们观察到(7.130)就是小波函数关于尺度函数加权和的形式，

$\psi(x)=\sum_{k\in\mathbf{Z}} h_{\psi}(k) \sqrt{2} \varphi(2 x-k)\tag{7.130}$

$\psi\left(2^{j} x-k\right)=\sum_{m} h_{\psi}(m-2 k) \sqrt{2} \varphi\left(2^{j+1} x-m\right)$

其中， $m\in Z$ ，于是我们可以得到

$d_{j}(k)=\int f(x) 2^{j / 2}\left[\sum_{m} h_{\psi}(m-2 k) \sqrt{2} \varphi\left(2^{j+1} x-m\right)\right] d x$

交换积分和求和的次序，可以得到

$\begin{aligned} d_{j}(k)&=\sum_{m} h_{\psi}(m-2 k) \int f(x) 2^{(j+1) / 2} \varphi\left(2^{j+1} x-m\right) d x\\ &=\sum_{m} h_{\psi}(m-2 k) c_{j+1}(m) \end{aligned}$

clc; clear all; close all; 
f=imread('4.一幅512×512的图像.tif'); 
f=im2double(f); 
[cA,cH,cV,cD]=dwt2(f, 'haar'); 
cA=mat2gray(cA); 
cH=mat2gray(cH); 
cV=mat2gray(cV); 
cD=mat2gray(cD); 
w=[cA,cH;cV,cD];
figure; imshow(w);