最长递增子序列、最长连续递增序列、最长重复子数组
- 最长递增子序列
- 1.方法
- 图解步骤
- 递归代码
- 最长连续递增序列
- 1.动态规划的方法
- 图解步骤
- 代码
- 最长重复子数组
- 图解步骤
- 代码
最长递增子序列
力扣连接:300. 最长递增子序列(中等)
1.方法
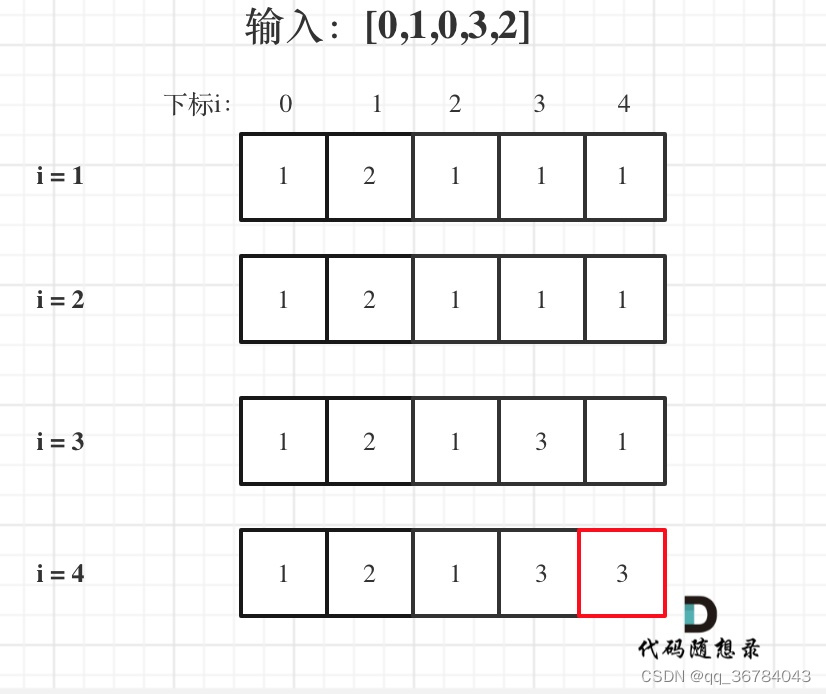
- dp[i]的定义
本题中,正确定义dp数组的含义十分重要。
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度
图解步骤
关键点:
- dp[i]的初始化,每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.
递归代码
class Solution {
public int lengthOfLIS(int[] nums) {
int size = nums.length;
int[] dp = new int[size];//以nums[i]为结尾的最长递增子序列的长度
Arrays.fill(dp, 1);
for(int i=1; i<size; i++){
for(int j=i-1; j>=0; j--){
if(nums[i]>nums[j]){
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
}
int max = Integer.MIN_VALUE;
for(int i=0;i<size;i++){
max = Math.max(max, dp[i]);
}
return max;
}
}
最长连续递增序列
力扣连接:674. 最长连续递增序列(简单)
1.动态规划的方法
- 确定dp数组(dp table)以及下标的含义
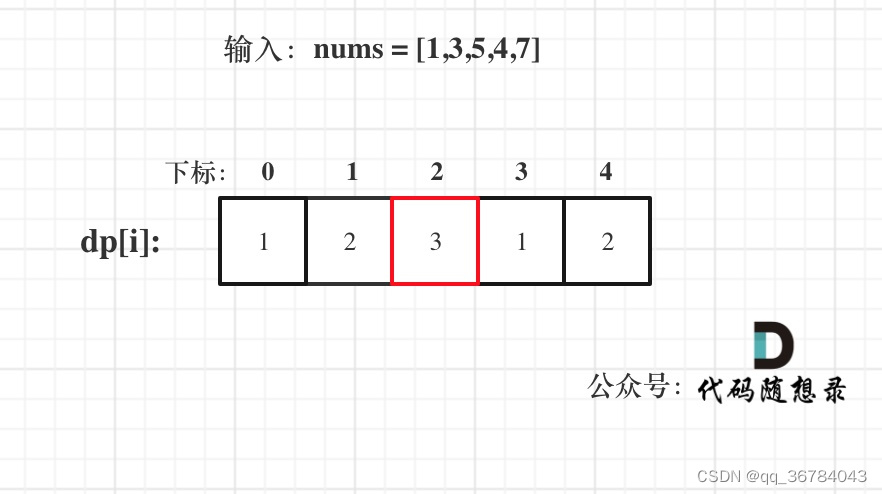
dp[i]:以下标i为结尾的连续递增的子序列长度为dp[i]。
图解步骤
关键点:
- 递推公式:dp[i] = dp[i - 1] + 1;
代码
class Solution {
public int findLengthOfLCIS(int[] nums) {
int size = nums.length;
int[] dp = new int[size];
Arrays.fill(dp, 1);
for(int i=1;i<size;i++){
if(nums[i]>nums[i-1]){
dp[i] = dp[i-1]+1;
}
}
int max = Integer.MIN_VALUE;
for(int i=0; i<size; i++){
max = Math.max(max, dp[i]);
}
return max;
}
}
最长重复子数组
力扣连接:718. 最长重复子数组(中等)
- 确定dp数组(dp table)以及下标的含义
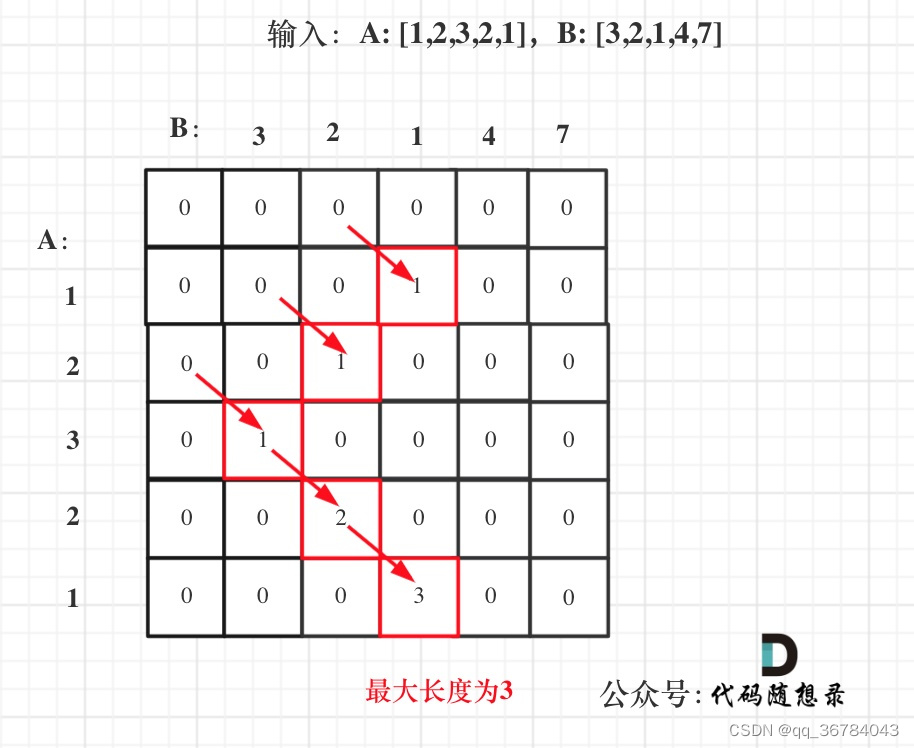
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]。 (特别注意: “以下标i - 1为结尾的A” 标明一定是 以A[i-1]为结尾的字符串 )方便下面代码编程
图解步骤
关键点:
- 初始化 默认dp[i][0]=0; dp[0][j]=0;
代码
class Solution {
public int findLength(int[] nums1, int[] nums2) {
int size1 = nums1.length;
int size2 = nums2.length;
int[][] dp = new int[size1+1][size2+1]; //定义dp数组中以i-1为结尾和以j-1为结尾的最大子数组长度
//初始化 默认dp[i][0]=0; dp[0][j]=0;
//因为i-1和j-1为结尾第一行第一列没有意义
int max = 0;
for(int i=1;i<=size1;i++){
for(int j=1;j<=size2;j++){
if(nums1[i-1]==nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
if(dp[i][j]>max){
max = dp[i][j];
}
}
}
}
return max;
}
}