这是一道 简单 题
https://leetcode.cn/problems/symmetric-tree/

题目

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

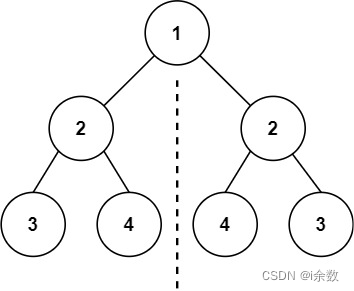
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2:

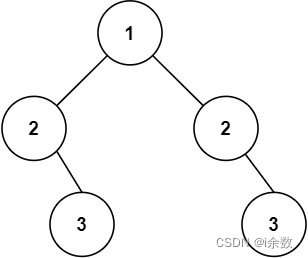
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 $[1,1000]$ 内
• $-100<=Node.val<=100$

---

题解

判断是否是对称二叉树，需要满足其 左子树 和 右子树 是对称的。

那么如何判断左右子树是对称的呢？

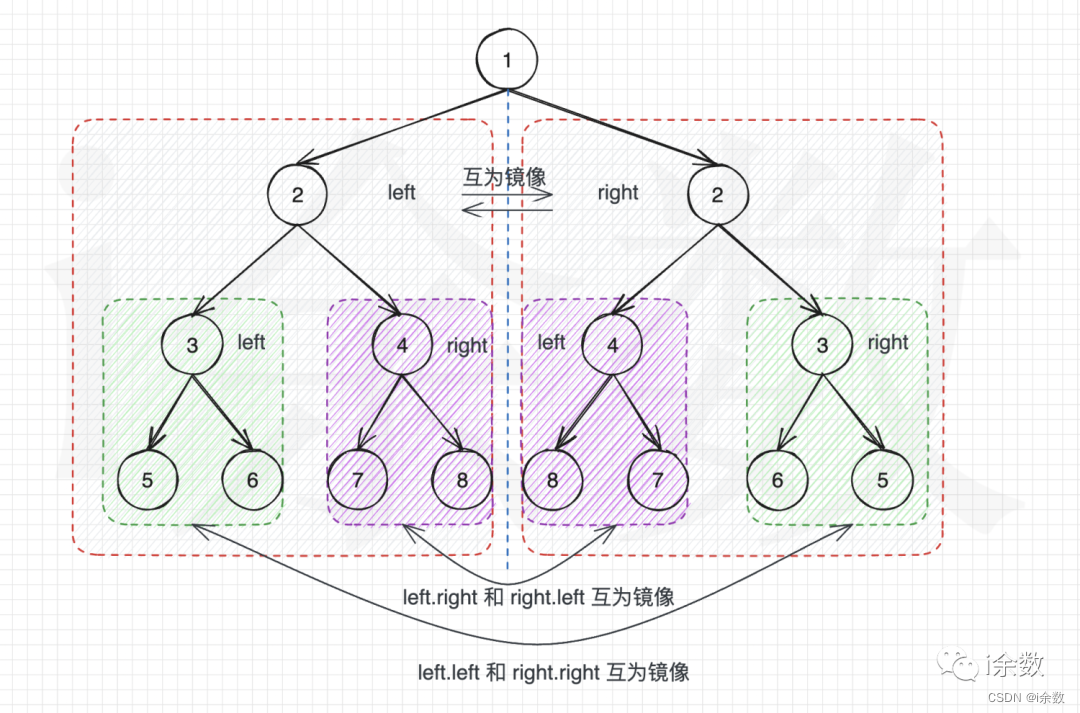
通过上图示例，我们可以分析出左右子树对称需要满足以下 3 个条件：

1. 左右子树根节点的值必须相等。如图所示左右子树的根节点都是 2 。
2. 左子树的左子树 和 右子树的右子树 必须对称。图中的绿色虚线框起来的部分。
3. 左子树的右子树 和 右子树的左子树 必须对称。图中的紫色虚线框起来的部分。

我们发现，判断两个树是否对称，其最终结果依赖另外的两组（条件2和3）的两个树是否对称，这就是典型的递归的思路，其中：

递归函数：判断两个二叉树是否对称。

边界条件：两个二叉树中任意一个为空，就可以返回。如果两个都为空返回 true，否则就是一个为空而另一个不为空返回 false。

Java 代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {

        if(root == null){
            return true;
        }

        return isSymmetric(root.left, root.right);

    }

    private boolean isSymmetric(TreeNode left, TreeNode right){
        if(left == null && right == null){
            return true;
        }else if(left == null || right == null){
            return false;
        }

        return left.val == right.val && isSymmetric(left.left, right.right) && isSymmetric(left.right, right.left);
    }
}

Go 代码实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func isSymmetric(root *TreeNode) bool {
    if root == nil {
        return true
    }
    return isSymmetric2(root.Left, root.Right)
}

func isSymmetric2(left *TreeNode, right *TreeNode) bool {
    if left == nil && right == nil {
        return true
    }else if left == nil || right == nil {
        return false
    }

    return left.Val == right.Val && isSymmetric2(left.Right, right.Left) && isSymmetric2(left.Left, right.Right)
}

复杂度分析

时间复杂度：$O(N)$。N 为二叉树中的节点个数。每个节点都需要计算一次，总计是 N 次。

空间复杂度：$O(N)$。空间复杂度取决于调用栈的深度，最差为 N。