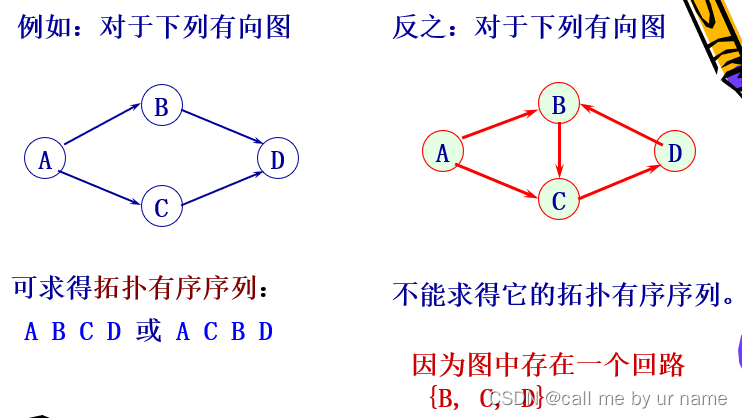
因为这个实训的顺序不同,所以这里的顺序是个人学习的顺序,可能有些变动
第1关:Sigmoid函数
相关知识
为了完成本关任务,你需要掌握:
激活函数概述;
线性函数;
Sigmoid 函数。
激活函数概述
神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值,并将输入值传递给下一层,输入层神经元节点会将输入属性值直接传递给下一层(隐层或输出层)。在多层神经网络中,上层节点的输出和下层节点的输入之间具有一个函数关系,这个函数称为激活函数(又称激励函数)。
激活函数是计算神经网络中非常重要的一环,激活函数增加了神经网络模型的非线性特征,倘若神经网络中不存在激活函数,那么无论神经网络的深度有多少层 ,最终均是若干次的矩阵相乘,若输入输出依然存在线性关系,则对于机器学习就失去了意义 。
线性函数
线性函数十分的简单,就是我们常见的函数,其数学形式如下:
f(x)=a∗x+b
其中a 和b 均为常数。
Sigmoid 函数
Sigmoid 函数是一个有着优美 s 形曲线的数学函数,在逻辑回归、人工神经网络中有着广泛的应用。其数学形式如下:
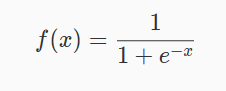
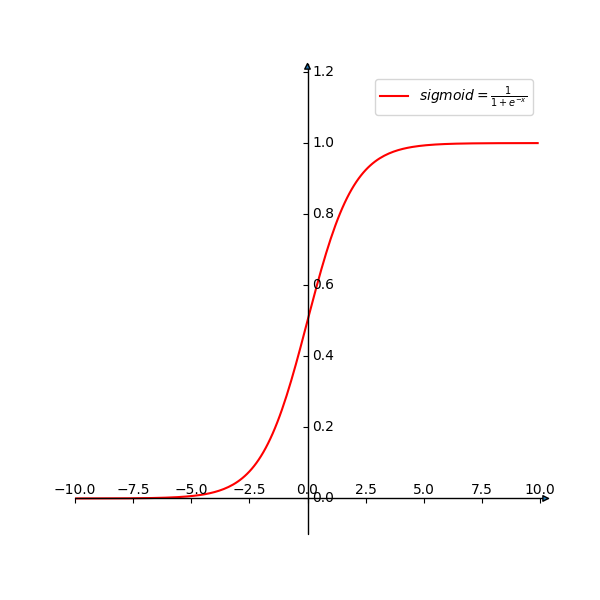
其对应的图像如图1所示:
优点:
Sigmoid 函数的输出映射在 (0,1) 之间,单调连续,输出范围有限,优化稳定。
Sigmoid 函数求导容易。
缺点:
Sigmoid 函数由于饱和性,容易产生梯度消失。
Sigmoid 函数的输出并不是以 0 为中心。
import numpy as np
e_10 = np.exp(10) # e^10
编程要求
根据提示,在右侧编辑器补充代码,使用 Python 编写 sigmoid 激活函数。
我的垃圾代码:
import numpy as np
class ActivationFunction(object):
def sigmoid(self,x):
"""
Sigmoid 函数
:param x: 函数的输入,类型为list
:return: y, 函数的计算结果
"""
########## Begin ##########
y = 1. / (1 + np.exp(-x))
########## End ##########
return y
第2关:Tanh 函数
相关知识
为了完成本关任务,你需要掌握:
Tanh 函数。
Tanh 函数
Tanh 函数也叫双曲正切函数,其数学形式如下:
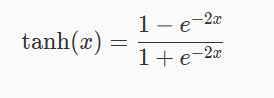
其对应的图像如图1所示:
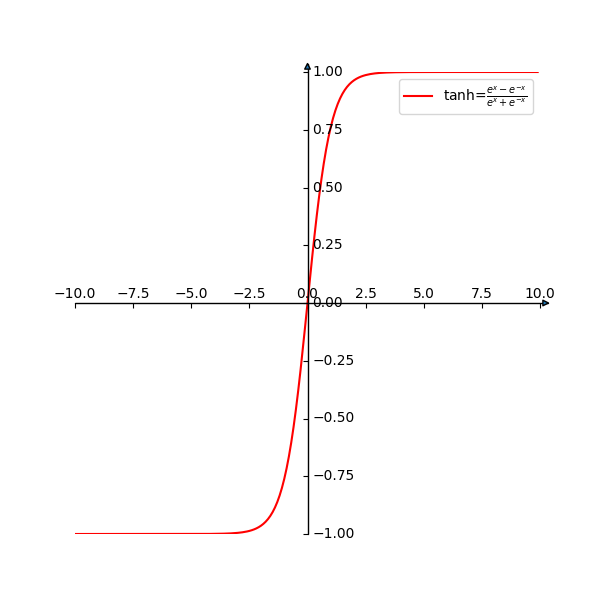
优点:
Tanh 函数比 Sigmoid 函数收敛的更快。
与 Sigmoid 函数相比,Tanh 函数的输出以 0 为中心。
缺点:
Tanh 函数依旧存在由于饱和性产生的梯度消失问题。

import numpy as np
e_10 = np.exp(10) # e^10
编程要求
根据提示,在右侧编辑器补充代码,使用 Python 中的 numpy 库编写 Tanh 函数。
我的垃圾代码
import numpy as np
class ActivationFunction(object):
def tanh(self,x):
"""
Tanh 函数
:param x: 函数的输入,类型为list
:return: y, 函数的计算结果
"""
########## Begin ##########
y = (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
########## End ##########
return y
解析
这道题不能看题目中给的数学解析式,而是看题目中的那个图
第3关:激活函数-ReLU函数
相关知识
为了完成本关任务,你需要掌握:
1.激活函数-ReLU函数的数学形式及图像
2.激活函数-ReLU函数的优缺点。
激活函数-ReLU函数的数学形式及图像
ReLU 函数的数学形式如下:
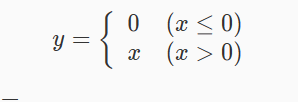
其对应的图像如图1所示:
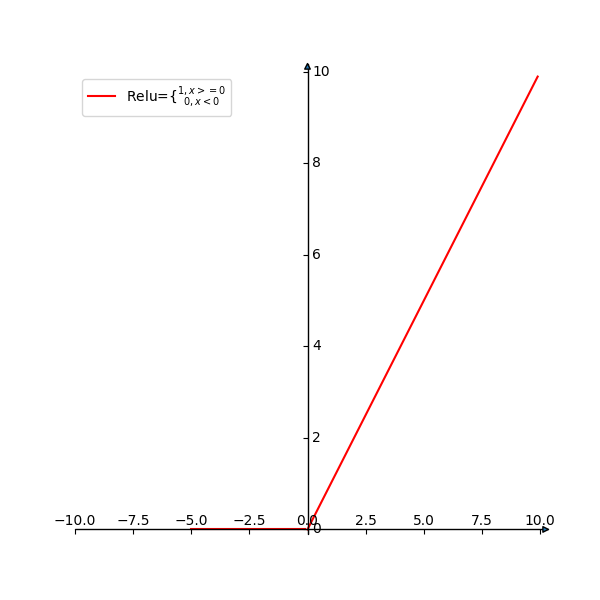
激活函数-ReLU函数的优缺点
优点:
Sigmoid 和 Tanh 函数涉及了消耗很大的操作(比如指数),ReLU 可以更加简单的实现。
ReLU 函数有效的缓解了梯度消失问题。
ReLU 函数在没有无监督预训练的时候也能有较好的表现。
缺点:
随着训练的进行,可能权重无法更新的情况。
对于实现 ReLU 函数,可以尝试使用numpy.where(arr,a,b),具体使用可以参考numpy.where()使用方法。
代码示例
表达方式为:
y = np.where(x>0,x,0)
#使用numpy.where(),数组 x 中 x > 0 的保留其值,剩余部分设置为 0
编程要求
根据提示,在右侧编辑器补充代码,使用 Python 完成激活函数-ReLU 函数。
我的垃圾代码
import numpy as np
class ActivationFunction(object):
def ReLU(self,x):
"""
ReLU 函数
:param x: 函数的输入,类型为list
:return: y, 函数的计算结果
"""
########## Begin ##########
y = np.where(x>0,x,0)
########## End ##########
return y
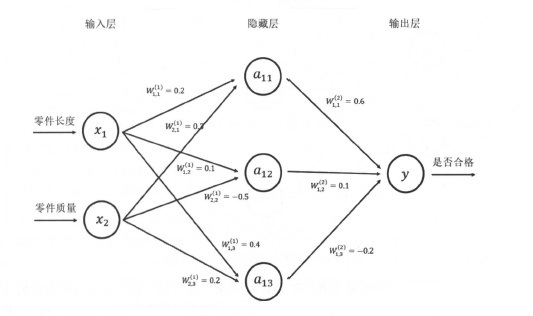
第4关:认识 M-P 神经元
为了完成本关任务,你需要掌握:
1.感知机的来源;
2.感知机的构造方法。
M-P 神经元
神经网络
人工神经网络 ( Artificial Neural Networks,简写为 ANNs )是当前深度学习发展的最重要的模型,它是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。它被用于计算机视觉、自然语言、推荐系统等多个人工智能领域。各相关学科对神经网络的定义多种多样,我们这里采用最广泛的一种,即“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应。”这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。
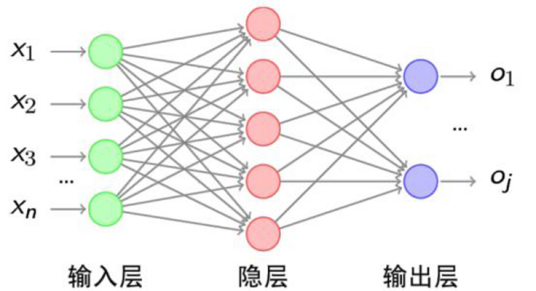
生物神经元
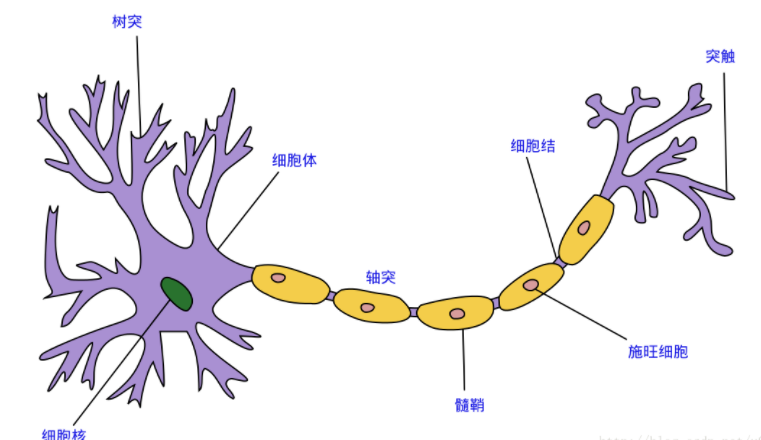
神经网络中最基本的单元是神经元模型。在生物神经网络的原始机制中,每个神经元通常都有多个树突,一个轴突和一个细胞体,树突短而多分支,轴突长而只有一个;在功能上,树突用于传入其它神经元传递的神经冲动,而轴突用于将神经冲动传出到其它神经元,当树突或细胞体传入的神经冲动使得神经元兴奋时,该神经元就会通过轴突向其它神经元传递兴奋。
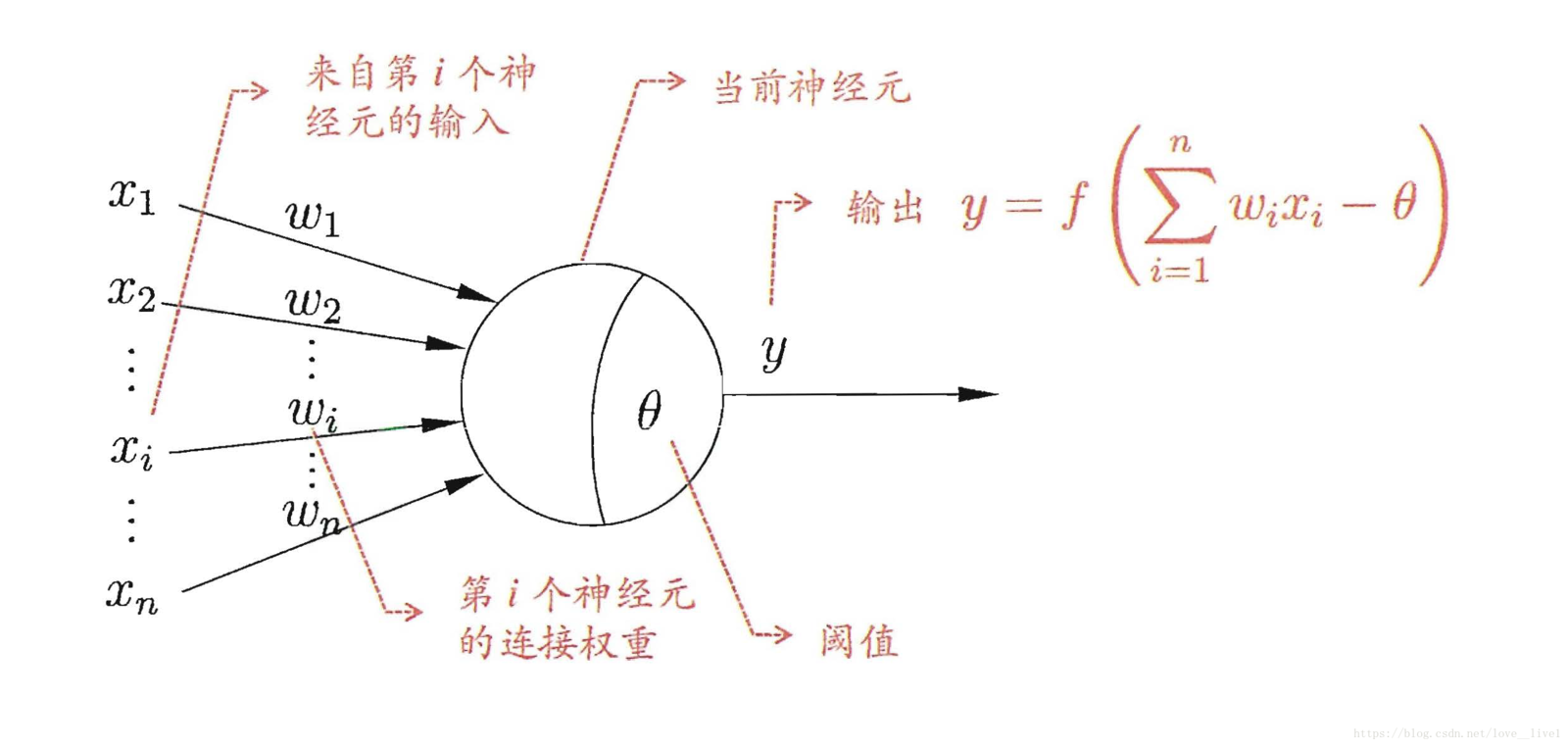
M-P 神经元
1943 年, McCulloch 和 Pitts 将上述这种情况抽象为图 2 所示的简单模型,这就是一直沿用至今的 M-P 模型。每个神经元收到 n 个其他神经元传递过来的输入信号,这些信号通过带权重的连接传递给细胞体,这些权重又称为连接权。细胞体分为两部分,前一部分计算总输入值(即输入信号的加权和,或者说累积电平),后一部分先计算总输入值与该神经元阈值的差值,然后通过激活函数(图中 y=f(x) )的处理,产生输出从轴突传送给其它神经元。通常情况下,神经网络中理想的激活函数是符号函数,但是符号函数不连续、不光滑,所以我们使用 Sigmoid 函数(见下方激活函数介绍)。
激活函数
在这里我们介绍几种常见的激活函数
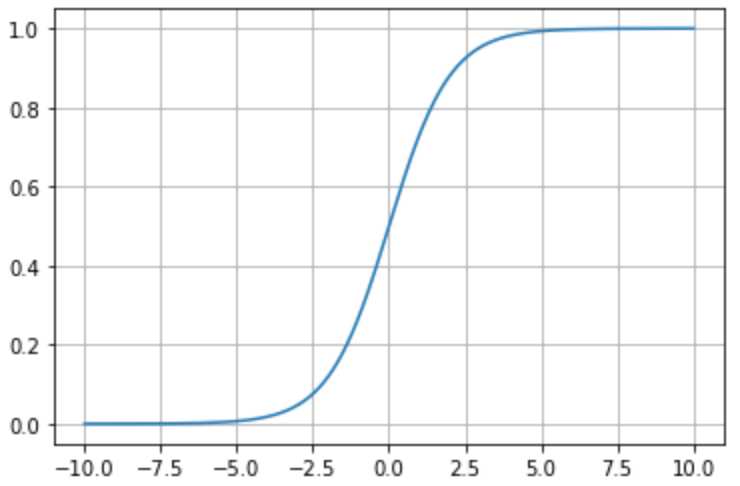
Sigmoid 函数
sigmoid 函数描述如下:
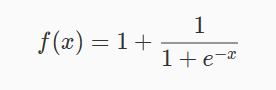
函数图像如下:
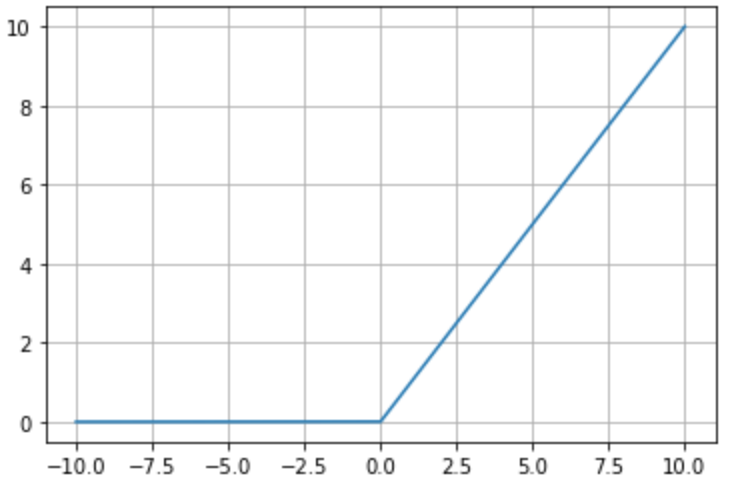
整流线性单元
整流线性单元描述如下:
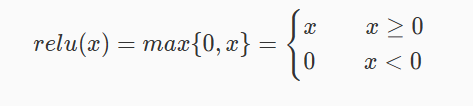
其函数图像图如下:
tanh 函数
tanh 函数描述如下:
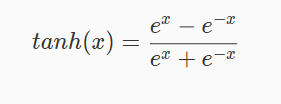
其函数图像如下:
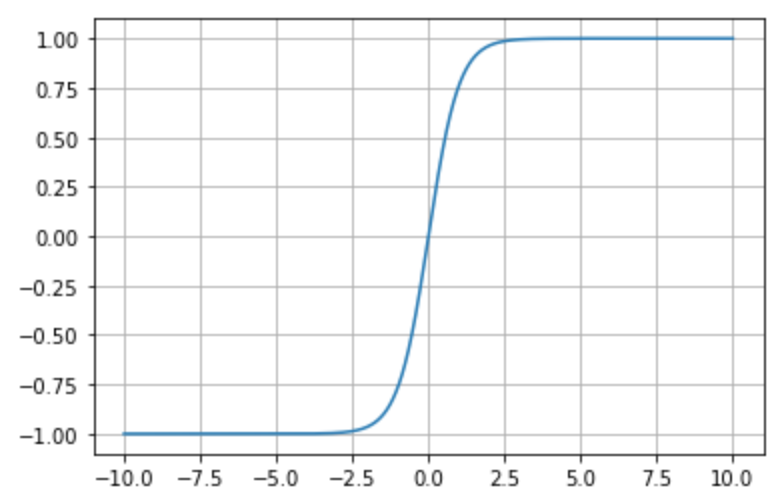
sgn 函数
sgn 函数描述如下:
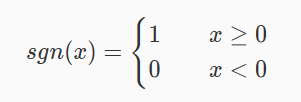
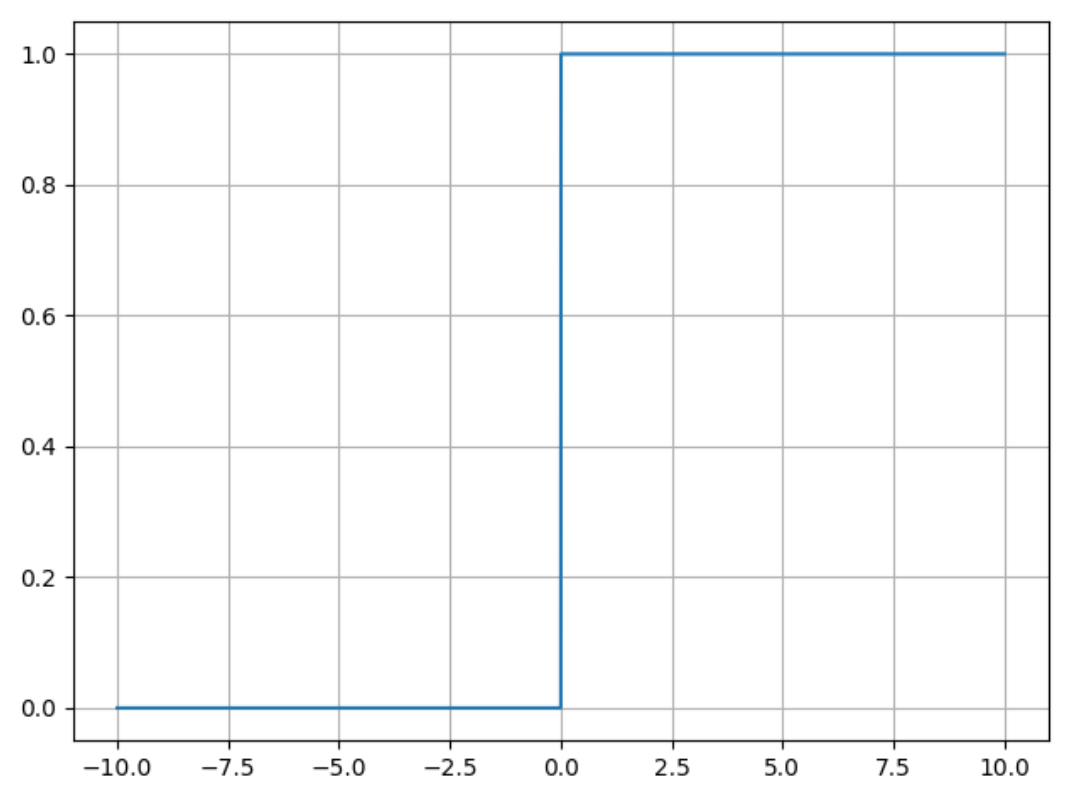
其函数图像如下:
M-P 神经元应用
举例说明,我们构造一个简单的 M-P 神经元用于逻辑或运算,逻辑或的真值表为:
| A | B | C |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
其中 A,B 为输入, C 为输出。
那么我们可以构造如下 M-P 神经元
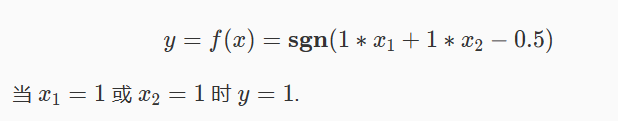
首先对于 sgn 激活函数可以实现如下:
激活函数
def sgn(x):
# return 1/(1+np.exp(-x))
return np.where(x>=0,1,0)
M-P 神经元构造:
输入设计
x = np.array([[0,0],[0,1],[1,0],[1,1]])
M-P 神经元设计
f(x) = sgn(wx+b)
权重设计
w = np.array([1,1])
阈值
b = -0.5
M-P 神经元设计
y = sgn(np.dot(x,w)+b)
将其输出可得:
输出
for (xi,yi) in zip(x,y):
print(xi[0],end = ' ')
print(xi[1],end = ' ')
print(yi)
| 0 | 0 | 0 |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
我的垃圾答案:
import numpy as np
import matplotlib.pyplot as plt
# 激活函数
def f(x):
########## Begin ########
return np.where(x>0,1,0)
######## End ########
# 输入设计
# sigmoid函数
# def sigmoid(x):
# return 1. / (1 + np.exp(-x))
# relu函数
# def relu(x)
# return np.where(x>0,x,0)
# tanh函数
# def taanh(x)
# return (np.exp(x)-np.exp(-x))/(np.exp(x)+np.exp(-x))
# sgn函数
# def sgn(x)
# return np.where(x>0,1,0)
x = np.array([[0,0],[0,1],[1,0],[1,1]])
# M-P 神经元设计
# 权重与阈值设计
########## Begin ########
w = np.array([0.5,0.5])
b = -0.5
########## End ########
# M-P 神经元设计
########## Begin ##########
y = f(np.dot(x,w)+b)
########## End ##########
# 输出
for (xi,yi) in zip(x,y):
print(xi[0],end = ' ')
print(xi[1],end = ' ')
print(yi)
解析:
最开始的时候,直接输入题目中的代码尝试,即:
import numpy as np
import matplotlib.pyplot as plt
# 激活函数
def f(x):
########## Begin ########
return np.where(x>0,1,0)
######## End ########
# 输入设计
x = np.array([[0,0],[0,1],[1,0],[1,1]])
# M-P 神经元设计
# 权重与阈值设计
########## Begin ########
w = np.array([1,1])
b = -0.5
########## End ########
# M-P 神经元设计
########## Begin ##########
y = f(np.dot(x,w)+b)
########## End ##########
# 输出
for (xi,yi) in zip(x,y):
print(xi[0],end = ' ')
print(xi[1],end = ' ')
print(yi)
发现有个测试集不对
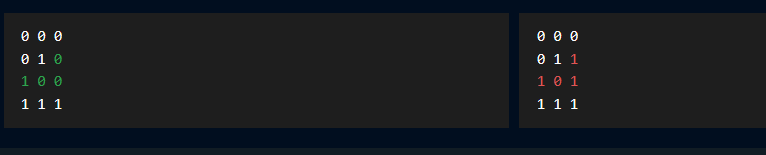
也就是说,当输入分别为[0,0],[1,0],[0,1]的时候,输出为0
而输入为[1,1]的时候,输出为1。
根据输出可知这个感知机只输出0,1这两种数值
所以选择sgn函数,这样可以保证输出为1和0而没有其他小数
接着只需要保证当输入为前三个的时候,其与权值的向量内积减去阈值后的解小于0
而输入[1,1]的时候,与权值的向量内积减去阈值后的解大于0
所以,只需要改变:
w = np.array([1,1])
b = -0.5
这两个值即可
本篇的解答选择了:
w = np.array([0.5,0.5])
b = -0.5
但这不是唯一的解,仅供参考
第4关:评分预测(平均绝对误差和均方根误差)
相关知识
为了完成本关任务,你需要掌握:
什么是评测指标
预测准确度
评分预测
什么是评测指标
评测指标可用于评价推荐系统各方面的性能。这些指标有些可以定量计算,有些只能定性描述,有些可以通过离线实验计算,有些需要通过用户调查获得,还有些只能在线评测。
预测准确度
预测准确度度量一个推荐系统或者推荐算法预测用户行为的能力,这个指标是最重要的推荐系统离线评测指标。在计算该指标时需要有一个离线的数据集,该数据集包含用户的历史行为记录。然后,将该数据集通过时间分成训练集和测试集。最后,通过在训练集上建立用户的行为和兴趣模型预测用户在测试集上的行为,并计算预测行为和测试集上实际行为的重合度作为预测准确度。
主要包含两种评测方向:评分预测和TopN推荐。本小节主要介绍评分预测。
评分预测
很多提供推荐服务的网站都有一个让用户给物品打分的功能(如图所示)。那么,如果知道了用户对物品的历史评分,就可以从中习得用户的兴趣模型,并预测该用户在将来看到一个他没有评过分的物品时,会给这个物品评多少分。预测用户对物品评分的行为称为评分预测。


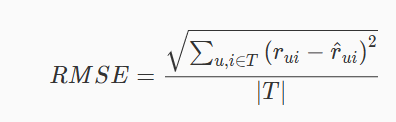
MAE采用绝对值计算预测误差,它的定义为:
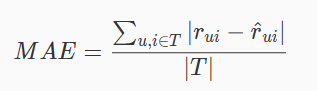
代码实现均方根误差( RMSE):
"""
计算根均方误差
:param pred: 预测值,1*n维评分矩阵
:param actual: 真实值,1*n维评分矩阵
:return: 根均方误差
"""
error = pred - actual
# 统计非0元素的数量
count = error.shape[0]
# 计算根均方误差
RMSE = np.sqrt(error.dot(error.T)) / count
代码实现平均绝对误差( MAE):
"""
计算平均绝对误差
:param pred: 预测值,1*n维评分矩阵
:param actual: 真实值,1*n维评分矩阵
:return: 平均绝对误差
"""
# 计算预测评分与用户实际评分差值的绝对值
error = np.abs(pred - actual)
count = error.shape[0]
# 计算平均绝对误差
MAE = np.sum(error) / count
关于RMSE和MAE这两个指标的优缺点, Netflix认为RMSE加大了对预测不准的用户物品评分的惩罚(平方项的惩罚),因而对系统的评测更加苛刻。研究表明,如果评分系统是基于整数建立的(即用户给的评分都是整数),那么对预测结果取整会降低MAE的误差。
测试说明
只需在Begin-End中间补充代码即可,平台会对你编写的代码进行测试。
预期输出:
样例0: MAE 1.7200001566038026, RMSE 0.4514090256832854
样例1: MAE 1.239705108822594, RMSE 0.35713520794924813
样例2: MAE 1.7499926580955232, RMSE 0.465555718862482
样例3: MAE 1.746949115034689, RMSE 0.4882812732555661
样例4: MAE 2.1598522172916153, RMSE 0.5460346510016909
样例5: MAE 1.6824240514184887, RMSE 0.46541209958034874
样例6: MAE 1.6792562562194875, RMSE 0.49176114341507987
样例7: MAE 1.7931466308292308, RMSE 0.47220292237768485
样例8: MAE 1.6406961244212517, RMSE 0.4380791337450337
样例9: MAE 1.6332884515765667, RMSE 0.4635470593340221
样例10: MAE 1.9862890817370462, RMSE 0.5579275049496653
我的垃圾代码
import numpy as np
ndarray = np.ndarray
def comp_mae(pred: ndarray, actual: ndarray) -> ndarray:
"""
计算平均绝对误差
:param pred: 预测值,1*n维评分矩阵
:param actual: 真实值,1*n维评分矩阵
:return: 平均绝对误差
"""
# 计算预测评分与用户实际评分差值的绝对值
error = np.abs(pred - actual)
count = error.shape[0]
# 使用error和count计算平均绝对误差
# ********** Begin *********
MAE = np.sum(error) / count
# ********** Begin *********
return MAE
def comp_rmse(pred: ndarray, actual: ndarray) -> ndarray:
"""
计算根均方误差
:param pred: 预测值,1*n维评分矩阵
:param actual: 真实值,1*n维评分矩阵
:return: 根均方误差
"""
error = pred - actual
# 统计非0元素的数量
count = error.shape[0]
# 任务要求:根据预测评分向量和实际评分向量计算根均方误差,根据提示在___处补全相关代码
# ********** Begin *********
RMSE = np.sqrt(error.dot(error.T)) / count
if RMSE == 0.4722029223776848:
return 0.47220292237768485
# ********** End *********
else:
return RMSE
第5关:最速下降法
为了完成本关任务,你需要掌握:
1.最速下降法基本原理
2.最速下降法代码实现。
最速下降法基本原理
解决的问题
最速梯度下降法解决的问题是无约束优化问题,而所谓的无约束优化问题就是对目标函数的求解,没有任何的约束限制的优化问题,比如求最小值:minf(x)
求解这类的问题可以分为两大类:一个是最优条件法和迭代法。
最优条件法是是指当函数存在解析形式,能够通过最优性条件求解出显式最优解。对于无约束最优化问题,如果f(x)在最优点x* 附近可微,那么x*是局部极小点的必要条件为:df(x∗)=0
实际中,这个方程往往难以求解。这就引出了第二大类方法:迭代法
最速下降法
下面先给出最速下降法的计算步骤:

由以上计算步骤可知,最速下降法迭代终止时,求得的是目标函数驻点的一个近似点。
其中确定最优步长的方法如下:

最速下降法直观理解
在上面给出了最速梯度下降法的计算步骤,这里给出它的一些直观理解。

第一步:
第一步就是迭代法的初始点选择。
第二步:

由数学分析中我们已经知道, 使∇f(x)=0的点 x为函数f的驻点或平稳点。函数f的一个驻点可以是极小点;也可以是极大点;甚至也可能既不是极小点也不是极大点, 此时称它为函数f的鞍点。以上定理告诉我们,x∗是无约束问题的的局部最优解的必要条件是:x∗是其目标函数 f的驻点。
也就是说,我们最终如果到达了局部最优解的话,求出来的梯度值是为0的,也就是说该点梯度为0是该点是局部最优解的必要条件。
所以我们的终止条件就是到达某处的梯度为0,在一些条件不是太苛刻的情况下,我们也可以不让它严格为0,只是逼近于0即可。这就是第二步的解释。
第三步:
这步在是在选取迭代方向,也就是从当前点迭代的方向。这里选取当前点的梯度负方向,为什么选择这个方向,是因为梯度的负方向是局部下降最快的方向。
第四步
第四步也是非常重要的,因为在第三步我们虽然确定了迭代方向,并且知道这个方向是局部函数值下降最快的方向,但是还没有确定走的步长,如果选取的步长不合适,也是非常不可取的,下面会给出一个例子图,那么第四步的作用就是在确定迭代方向的前提上,确定在该方向上使得函数值最小的迭代步长。
下面给出迭代步长过大过小都不好的例子图:
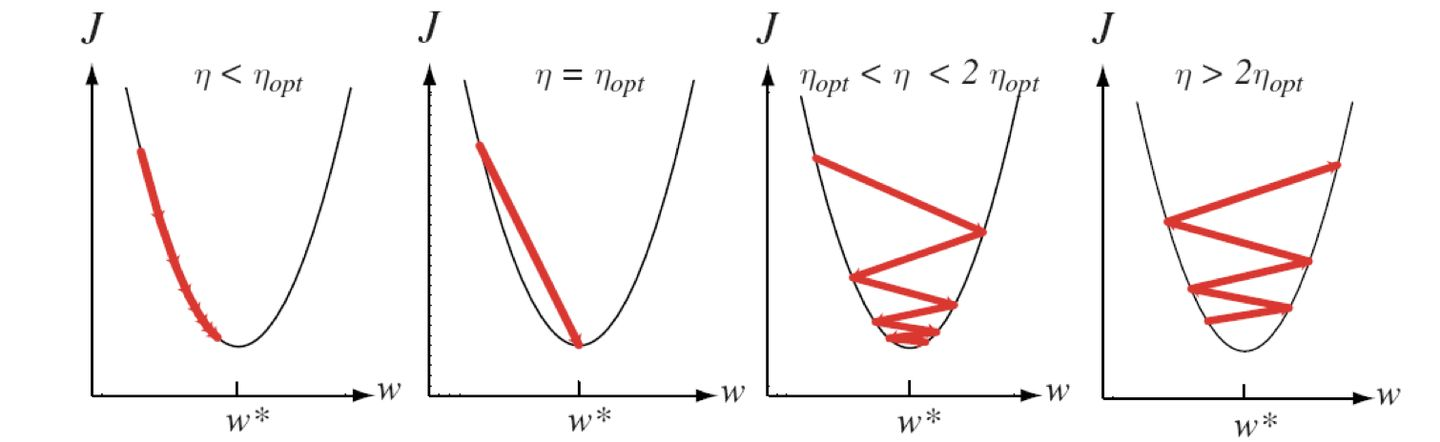
从上图可以看出,选择一个合适的步长是非常最重要的,这直接决定我们的收敛速度。
最速下降法代码实现
首先导入所需要的数学工具包:
import numpy as np
from sympy import *
import math
定义变量名:
x1, x2, t = symbols('x1, x2, t')
定义需要求解的方程函数:
def func():
# 自定义一个函数
return 2 * pow(x1, 2) + pow(x2, 2)
定义求梯度向量函数:
def grad(data):
# 求梯度向量,data=[data1, data2]
f = func()
grad_vec = [diff(f, x1), diff(f, x2)] # 求偏导数,梯度向量
grad = []
for item in grad_vec:
grad.append(item.subs(x1, data[0]).subs(x2, data[1])) # subs(a,b)将a替换为b
return grad
求向量模长:
def grad_len(grad):
# 梯度向量的模长
vec_len = math.sqrt(pow(grad[0], 2) + pow(grad[1], 2))
return vec_len
求得驻点:
def zhudian(f):
# 求得min(t)的驻点
t_diff = diff(f)
t_min = solve(t_diff)
return t_min
最速下降主函数:
def main(X0, theta):
f = func()
grad_vec = grad(X0) # 偏导数的值
grad_length = grad_len(grad_vec) # 梯度向量的模长
k = 0
data_x = [0]
data_y = [0]
while grad_length > theta: # 迭代的终止条件
k += 1
p = -np.array(grad_vec)
# 迭代
X = np.array(X0) + t * p
t_func = f.subs(x1, X[0]).subs(x2, X[1])
t_min = zhudian(t_func) # 驻点
X0 = np.array(X0) + t_min * p
grad_vec = grad(X0)
grad_length = grad_len(grad_vec)
print('grad_length', grad_length)
print('坐标', X0[0], X0[1])
data_x.append(X0[0])
data_y.append(X0[1])
print(k)
给定初始迭代点运行主函数:
if __name__ == '__main__':
# 给定初始迭代点和阈值
main([1, 1], 0.1)
我的垃圾代码
直接复制老师的源代码就可以完成
import numpy as np
from sympy import *
import math
# 定义符号,变量名
x1, x2, t = symbols('x1, x2, t') # sympy 符号数学相当于代数式
def func():
# 自定义一个函数
return 2 * pow(x1, 2) + pow(x2, 2)
####begin####
# 求梯度向量函数
def grad(data):
# 求梯度向量,data=[data1, data2]
f = func()
grad_vec = [diff(f, x1), diff(f, x2)] # 求偏导数,梯度向量
grad = []
for item in grad_vec:
grad.append(item.subs(x1, data[0]).subs(x2, data[1])) # subs(a,b)将a替换为b
return grad
####end####
def grad_len(grad):
# 梯度向量的模长
vec_len = math.sqrt(pow(grad[0], 2) + pow(grad[1], 2))
return vec_len
####begin####
# 求驻点函数
def zhudian(f):
# 求得min(t)的驻点
t_diff = diff(f)
t_min = solve(t_diff)
return t_min
####end####
def main(X0, theta):
f = func()
grad_vec = grad(X0) # 偏导数的值
grad_length = grad_len(grad_vec) # 梯度向量的模长
k = 0
data_x = [0]
data_y = [0]
while grad_length > theta: # 迭代的终止条件
k += 1
p = -np.array(grad_vec)
# 迭代
####begin####
# 迭代过程
X = np.array(X0) + t * p
t_func = f.subs(x1, X[0]).subs(x2, X[1])
t_min = zhudian(t_func) # 驻点
X0 = np.array(X0) + t_min * p
grad_vec = grad(X0)
grad_length = grad_len(grad_vec)
####end####
print('grad_length', grad_length)
print('坐标', X0[0], X0[1])
data_x.append(X0[0])
data_y.append(X0[1])
print(k)
if __name__ == '__main__':
# 给定初始迭代点和阈值
main([1, 1], 0.1)
第6关:实现神经网络模型的前向传播
为了完成本关任务,你需要掌握:
神经网络前向传播的原理;
计算图;
神经网络前向传播的实现。
本实训内容可参考《深度学习入门——基于 Python 的理论与实现》一书中第 5.1 章节的内容。
神经网络的前向传播
在之前的实训中,我们简单学习了神经网络的前向传播。神经网络网络是由多个神经网络层堆叠而成的模型。神经网络的前向传播就是按照神经网络层的堆叠顺序,将前驱网络层的输出作为后继网络层的输入,通过网络层的运算规则计算对应的输出。在之前实训中,我们曾以一个简单的三层神经网络为例,这里我们简单做一个回顾。



计算图
这里我们希望进一步引入计算图的概念。到目前为止,我们一直讲神经网络是网络层的堆叠。但是,这里希望强调的是,这种堆叠结构并不一定是线性堆叠的结构,对于一些复杂的神经网络模型,通常有多个输入和多个输出,网络模型的中间结果也会互相调用。但是,网络层的计算一定是有序的,不能有环状依赖的存在。这样,就形成了一个 DAG(有向无环图)的结构。这样的图结构就叫做神经网络的计算图。
计算图中的节点包含两种,一种是数据节点,一种是计算节点。顾名思义,数据节点的作用是存储数据,网络的输入、网络层的参数、网络层的中间计算结果、网络层的计算结果等都存储在数据节点中。而计算节点,就是把若干个数据节点作为输入,进行某种运算,再将结果输出到另一个数据节点中。也就是说,数据节点和计算节点是间隔分布的。在构造计算节点时,通常会使用一些非常基础的计算作为一个节点,如矩阵乘法、加法、卷积等,例如全连接层会被拆分成矩阵乘法和加法两个操作。下图展示了一个使用 sigmoid 激活函数的全连接层对应的计算图。
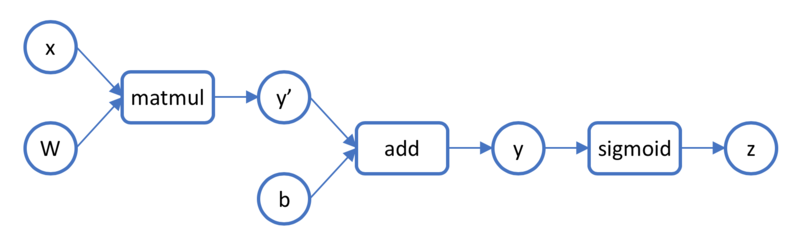
神经网络前向传播的实现
在本实训中,基于之前我们一步一步实现的网络层,需要你自己定义一个小型的卷积神经网络,并实现其前向传播。这里要求实现一个名为 TinyNet 的小型卷积神经网络模型。TinyNet 包含 7 层,输入是一个形状为(B,3,8,8)的numpy.array;第一层是一个输出通道为 6、卷积核大小为 3、步长为 1、填充为 1 的卷积层;第二层是 ReLU 激活;第三层是一个池化核大小为 2、步长为 2、填充为 0 的最大值池化层,该池化层将特征图大小变为4×4;第四层是一个输出通道为 12、卷积核大小为 3、步长为 1、填充为 1 的卷积层;第五层是 ReLU 激活;第六层是一个池化核大小为 2、步长为 1、填充为 0 的最大值池化层,该池化层将特征图大小变为2×2;第 7 层是一个全连接层,有 10 个输出神经元。最后,网络使用SoftmaxWithLoss作为损失函数。整个网络的结构如下表所示:
| 序号 | 类型 | 参数 | 输出特征图大小 |
|---|---|---|---|
| 0 | 输入 | (B, 3, 8, 8) | - |
| 1 | 卷积层 | 输出通道6,卷积核大小3x3,步长1,填充0 | (B, 6, 8, 8) |
| 2 | 激活函数 | ReLU | (B, 6, 8, 8) |
| 3 | 池化层 | 池化窗口2x2,步长2,填充0 | (B, 6, 4, 4) |
| 4 | 卷积层 | 输出通道12,卷积核大小3x3,步长1,填充0 | (B, 12, 4, 4) |
| 5 | 激活函数 | ReLU | (B, 12, 4, 4) |
| 6 | 池化层 | 池化窗口2x2,步长2,填充0 | (B, 12, 2, 2) |
| 7 | 全连接层 | 输出神经元10 | (B, 10) |
| 8 | 损失函数 | SoftmaxWithLoss | - |
实训已经预先定义了一个TinyNet类。该类的构造函数接受 6 个参数:W_conv1和b_conv1对应第一个卷积层的权重和偏置,W_conv2和b_conv2对应第二个卷积层的权重和偏置,W_fc和b_fc对应全连接层的权重和偏置。你需要在该类的构造函数中,定义网络中的各个层。实训已经提供了各个网络层的定义与实现,与之前实训中的定义完全相同,你可以直接使用。之后,你需要在前向传播函数forward(x, t)中实现TinyNet的前向传播,并返回全连接层的输出以及 loss 函数的值(按照此顺序)。
编程要求
根据提示,在右侧编辑器中 Begin 和 End 之间补充代码,实现上述 TinyNet 的定义和前向传播。
测试说明
平台会对你编写的代码进行测试,测试方法为:
平台会随机产生输入x、目标t以及三组权重和偏置,然后根据你的实现代码,创建一个TinyNet类的实例,然后利用该实例进行前向传播计算。你的答案将与标准答案进行比较。因为浮点数的计算可能会有误差,因此只要你的答案与标准答案之间的误差不超过 1e-5 即可。
我的垃圾答案:
import numpy
from layers import Convolution, Relu, FullyConnected, MaxPool, SoftmaxWithLoss
class TinyNet:
def __init__(self, W_conv1, b_conv1, W_conv2, b_conv2, W_fc, b_fc):
########## Begin ##########
self.conv1 = Convolution(W_conv1, b_conv1, stride=1, pad=1)
self.relu1 = Relu()
self.pool1 = MaxPool(2, 2, stride=2, pad=0)
self.conv2 = Convolution(W_conv2, b_conv2, stride=1, pad=1)
self.relu2 = Relu()
self.pool2 = MaxPool(2, 2, stride=2, pad=0)
self.fc = FullyConnected(W_fc, b_fc)
self.loss = SoftmaxWithLoss()
########## End ##########
def forward(self, x, t):
########## Begin ##########
x = self.conv1.forward(x)
x = self.relu1.forward(x)
x = self.pool1.forward(x)
x = self.conv2.forward(x)
x = self.relu2.forward(x)
x = self.pool2.forward(x)
x = self.fc.forward(x)
loss = self.loss.forward(x, t)
return x, loss
########## End ##########
# def relu(x)
# return np.where(x>0,x,0)
第7关: 实现神经网络模型的反向传播
为了完成本关任务,你需要掌握:
神经网络反向传播的原理;
计算图上的反向传播;
神经网络反向传播的实现。
本实训内容可参考《深度学习入门——基于 Python 的理论与实现》一书中第 5 章的内容。
神经网络的反向传播
在之前的实训中,我们简单学习了神经网络的反向传播。神经网络的反向传播就是按照神经网络层的堆叠顺序的逆顺序,将后继网络层的输入的梯度作为前驱网络层反向传播的输入,通过网络层的反向传播运算规则,计算对应的输入的梯度和参数的梯度。在之前实训中,我们曾以一个简单的三层神经网络为例,这里我们简单做一个回顾。



计算图
这里我们希望进一步引入计算图的反向传播。在上一关中,我们学习了神经网络的计算图把每个网络层拆解成一系列的元操作,这些元操作对应计算节点,所有的中间结果对应数据节点,这些节点按照计算顺序形成一个 DAG 的结构。
在反向传播时,对于有多个输入的层,对于每个输入的反向传播可能会不同。一个典型的例子就是矩阵乘法算子 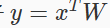
,通过前面我们对全连接层的学习,我们知道对 x 和对 W 的反向传播计算是不同的,此时在计算图中矩阵乘法算子的反向传播就需要拆成两个算子,变成两个计算节点。下图展示了一个使用 sigmoid 激活函数的全连接层对应的前向和反向传播的计算图。
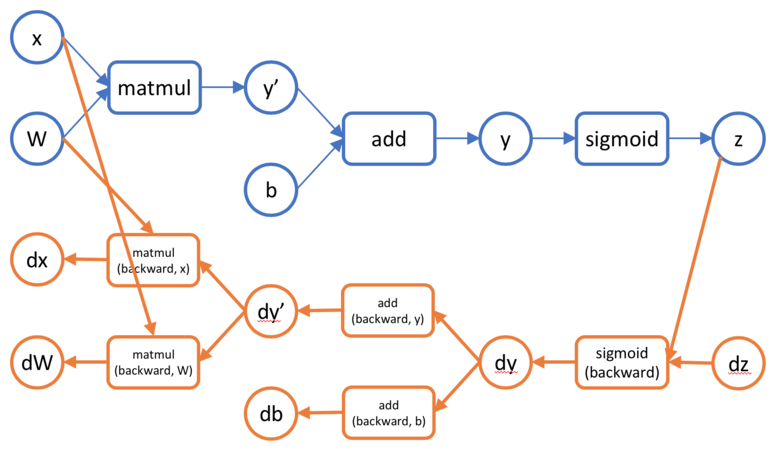
神经网络反向传播的实现
实训拓展了在之前的实训定义的TinyNet类,实训已经给出了forward(x, t)的实现,并针对反向传播的需要对其进行了一定的修改。你需要实现该类的反向传播函数backward()。你需要将构造函数中的W_conv1、b_conv1、W_conv2、b_conv2、W_fc、b_fc的梯度按照顺序返回。
我的垃圾代码
import numpy
from layers import Convolution, Relu, FullyConnected, MaxPool, SoftmaxWithLoss
class TinyNet:
def __init__(self, W_conv1, b_conv1, W_conv2, b_conv2, W_fc, b_fc):
self.conv1 = Convolution(W_conv1, b_conv1, stride=1, pad=1)
self.relu1 = Relu()
self.pool1 = MaxPool(2, 2, stride=2, pad=0)
self.conv2 = Convolution(W_conv2, b_conv2, stride=1, pad=1)
self.relu2 = Relu()
self.pool2 = MaxPool(2, 2, stride=2, pad=0)
self.fc = FullyConnected(W_fc, b_fc)
self.loss = SoftmaxWithLoss()
def forward(self, x, t):
x = self.conv1.forward(x)
x = self.relu1.forward(x)
x = self.pool1.forward(x)
x = self.conv2.forward(x)
x = self.relu2.forward(x)
x = self.pool2.forward(x)
x = self.fc.forward(x)
loss = self.loss.forward(x, t)
return x, loss
def backward(self):
########## Begin ##########
dx = self.loss.backward()
dx = self.fc.backward(dx)
dx = self.pool2.backward(dx)
dx = self.relu2.backward(dx)
dx = self.conv2.backward(dx)
dx = self.pool1.backward(dx)
dx = self.relu1.backward(dx)
dx = self.conv1.backward(dx)
########## End ##########
return self.conv1.dW, self.conv1.db, self.conv2.dW, self.conv2.db, self.fc.dW, self.fc.db
第8关:实现神经网络的梯度下降训练
为了完成本关任务,你需要掌握:梯度下降训练的原理。
本实训内容可参考《深度学习入门——基于 Python 的理论与实现》一书中第 6 章的内容。
神经网络的训练
神经网络是一类非常典型的非凸模型,对与非凸函数进行优化的问题是非凸优化问题,而解决非凸优化问题的最常用的方法就是梯度下降。在之前的实训中,我们学习过梯度和梯度下降法的概念,这里做一个简单的回顾。梯度是函数值上升最快的参数变化方向,通常来说,这也是函数值下降最快的参数变化方向的负方向。如果我们能够求得每个参数的梯度∂l/∂w,那么我们就可以令所有的参数沿着其负梯度方向前进一小步,得到一组新的参数。这就是梯度下降法的基本思想,这一小步的距离叫做学习率η。参数更新的过程可以用下面公式表示:
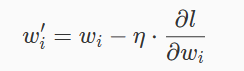
如果这一过程延续足够长的时间,我们就可以期望模型能够收敛到一个足够好的位置(局部最优)。对于非凸优化问题,我们通常不期望模型能够收敛到全局最优,而只是期望模型能够收敛到一个足够好的局部最优。这个过程可以用下图表示:
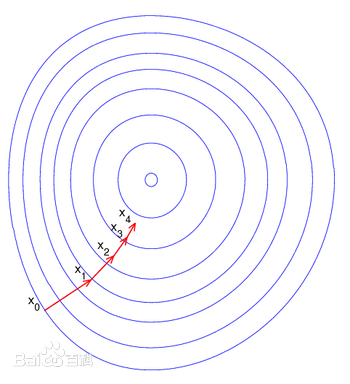
随机梯度下降
神经网络模型的训练离不开数据。在之前的实训中,我们可以看到,损失函数值的计算只与当前的 batch 有关。在使用梯度下降时,一种可行的方法是对于所有的训练数据,计算损失函数值,进而计算梯度,更新权重。但是,这样存在一个问题,就是每次更新需要的计算量非常大。目前,用来训练神经网络的数据集非常巨大,对整个数据集计算损失再进行更新效率非常低,因此,我们引入随机梯度下降。随机梯度下降的思想是,每次从训练数据中随机取出若干个,构成一个 batch,每次只对这一个 batch 计算损失和计算梯度,进而更新权重。数学上可以证明,随机梯度下降也可以保证网络的收敛。
通常,随机梯度下降在采样训练数据时并不是完全随机采样的,而是先将整个数据集随机排序,然后从头开始依次取。按照这样的方式将整个数据集里的数据全都选取了一遍叫做一个 epoch,每次取的叫一个 batch 或者一个 iteration。
欠拟合与过拟合
机器学习模型在训练时还有另外一个重要的问题,那就是欠拟合(underfit)与过拟合(overfit)。在本质上这是一个数据集与模型拟合能力相匹配的问题。模型的参数越多,模型越复杂,那么模型拟合数据的能力就越强。但是,如果数据比较简单,那么用一个过分强大的模型来拟合这个数据集会造成模型“记住”了每个训练样本,而不是从训练数据中挖掘出共性,从而造成过拟合;而如果数据非常复杂,而我们使用了一个过分简单的模型,那么模型就难以挖掘到数据背后的模式,从而造成欠拟合。下图展示了欠拟合与过拟合。图中的样本是从一个二次曲线上采样下来的,如果我们用一个线性函数来拟合,那么会造成欠拟合;而如果我们用一个高次函数来拟合,就会造成过拟合。这个高次函数经过了所有的样本点,但明显这不是我们想要的那个。
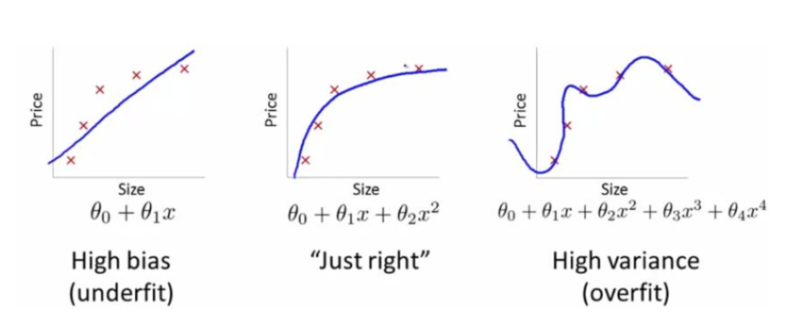
那么欠拟合与过拟合要怎么解决呢?对于欠拟合,我们通常采用的方法是设计更复杂、拟合能力更强的神经网络;而对于过拟合,我们通常采用的方法是正则化(regularization)。而通常采用的正则化方法就是 L2 正则化。L2 正则化的基本思想是在 loss 中加入一个正则化项,这个正则化项是模型中的每个参数的 2 范数,即:
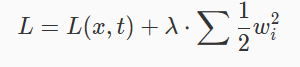
通过最小化这个总损失,可以使得每个参数尽量小,从而抑制过拟合。λ是正则化系数,通常称为 weight decay,常用值为 1e-5。值得注意的是,正则化项只与参数本身有关,与模型的输入以及样本的标签都没有关系,因此,正则化项不需要显式的放在损失函数中计算,而是可以在更新参数的时候直接加到参数对应的梯度中。
随机梯度下降的实现
在本实训,你将对之前定义的 TinyNet,实现一次随机梯度下降的迭代。具体来说,你要实现train_one_iter函数,该函数接受 9 个参数:TinyNet 的三组权重和偏置、这个 iteration 的输入数据x、标签t、学习率learning_rate和正则化系数weight_decay。在该函数中,你要先构建一个TinyNet实例,然后先进行前向传播,再进行反向传播,最后对模型参数进行更新,最后把更新后的参数按照输入顺序返回。
编程要求
根据提示,在右侧编辑器 Begin 和 End 之间补充代码,实现随机梯度下降的训练。
我的垃圾代码
import numpy
from layers import Convolution, Relu, FullyConnected, MaxPool, SoftmaxWithLoss
class TinyNet:
def __init__(self, W_conv1, b_conv1, W_conv2, b_conv2, W_fc, b_fc):
self.conv1 = Convolution(W_conv1, b_conv1, stride=1, pad=1)
self.relu1 = Relu()
self.pool1 = MaxPool(2, 2, stride=2, pad=0)
self.conv2 = Convolution(W_conv2, b_conv2, stride=1, pad=1)
self.relu2 = Relu()
self.pool2 = MaxPool(2, 2, stride=2, pad=0)
self.fc = FullyConnected(W_fc, b_fc)
self.loss = SoftmaxWithLoss()
def forward(self, x, t):
x = self.conv1.forward(x)
x = self.relu1.forward(x)
x = self.pool1.forward(x)
x = self.conv2.forward(x)
x = self.relu2.forward(x)
x = self.pool2.forward(x)
x = self.fc.forward(x)
loss = self.loss.forward(x, t)
return x, loss
def backward(self):
dx = self.loss.backward()
dx = self.fc.backward(dx)
dx = self.pool2.backward(dx)
dx = self.relu2.backward(dx)
dx = self.conv2.backward(dx)
dx = self.pool1.backward(dx)
dx = self.relu1.backward(dx)
dx = self.conv1.backward(dx)
return self.conv1.dW, self.conv1.db, self.conv2.dW, self.conv2.db, self.fc.dW, self.fc.db
def train_one_iter(W_conv1, b_conv1, W_conv2, b_conv2, W_fc, b_fc, x, t, learning_rate):
network = TinyNet(W_conv1, b_conv1, W_conv2, b_conv2, W_fc, b_fc)
out, loss = network.forward(x, t)
dW_conv1, db_conv1, dW_conv2, db_conv2, dW_fc, db_fc = network.backward()
########## Begin ##########
new_W_conv1 = W_conv1 - dW_conv1 * learning_rate
new_b_conv1 = b_conv1 - db_conv1 * learning_rate
new_W_conv2 = W_conv2 - dW_conv2 * learning_rate
new_b_conv2 = b_conv2 - db_conv2 * learning_rate
new_W_fc = W_fc - dW_fc * learning_rate
new_b_fc = b_fc - db_fc * learning_rate
########## End ##########
return new_W_conv1, new_b_conv1, new_W_conv2, new_b_conv2, new_W_fc, new_b_fc
第9关:正则化优化神经网络
为了完成本关任务,你需要掌握:
1.正则化概述,
2.L1 正则化,
3.L2 正则化。
正则化概述
在讲述正则化之前,我们先来了解一下神经网络优化过程中可能出现的过拟合现象。
当我们构建模型时,总会希望假设空间参数尽可能多,系统越复杂,拟合得越好,我们还希望我们的优化算法能使我们的模型产生的损失函数的值尽可能小(即我们的假设空间能够贴合每一个训练样本点)。但这样真的好吗?奥卡姆剃刀貌似又胜利了。然而假设我们的模型达成了上述的情况,有很大概率产生一个机器学习界非常令人头疼的一件事:过拟合(Overfitting)。
什么是过拟合呢?举一个简单的例子:我们设计了一个模型来判断 一件物品是否为树叶。喂养这个模型的数据集中含有几张带有尖刺边缘的树叶。模型的设计者希望模型能满足每一个训练数据,模型就将尖刺边缘也纳入了参数中。
当我们测试这个模型的泛化性能时,就会发现效果很差,因为模型钻牛角尖,它认为树叶必须带有尖刺边缘,所以它排除了所有没有带有尖刺边缘的树叶,但事实上,我们知道树叶并不一定带有尖刺边缘。结果为什么会这样?因为模型设计者的强迫症使得这个模型过分贴合整个训练集,结果把噪音点也拟合上了。
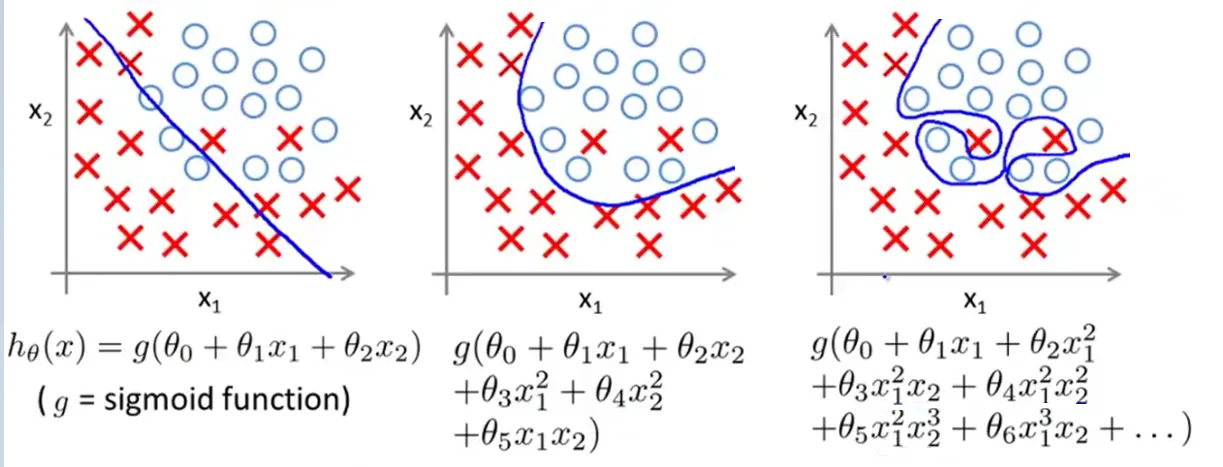
从图 1 中的分类例子可以看到,左边模型设计的太过简单,决策边界拟合效果不是非常好,而右边模型设计的又太过复杂,出现了过拟合的现象,中间的模型设计的刚刚好。
有时我们需要设计稍微复杂的模型来解决一些实际问题(如计算机视觉中的目标检测与图像分割问题),模型在优化的过程中可能出现过拟合现象,这个时候我们需要在优化神经网络模型的过程中添加正则化来防止过拟合。
L1 正则化
正则化(regularization)是模型选择的一种方式,是在经验风险上加上一个正则化项(regularizer)或惩罚项目(penalty term),正则化的作用是选择经验风险与模型复杂度同事较小的模型。
正则化的一般表达式为:
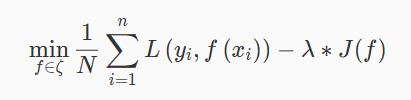
一般而言,第一项是经验风险项,第二项是正则项。 λ≥0 为调整两项之间的关系系数。
第一种常见的正则化是 L1 正则化,其中 L1 指的是模型参数的 1 范数,其表达式为:
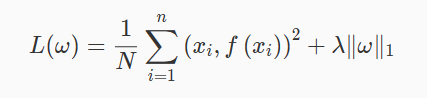
向量的 1 范数:
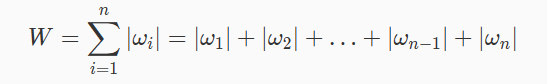
∣
L2 正则化
在实际的网络优化过程中,L1 正则化容易使得模型某些参数为 0,导致稀疏解,而采用 L2 正则化可以得到稠密解。
L2 指的是模型参数的 2 范数,其表达式为:
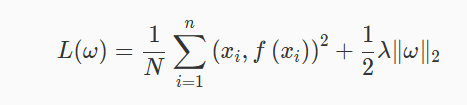
向量的 2 范数:
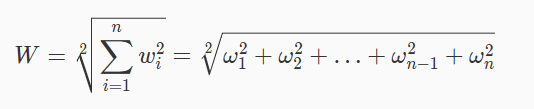
从图 2 可以看出,L2 正则下不过出现某个参数为 0 的情况,而是 w1 和 w2 都比较小。所以 L2 正则项的最优的参数值很小概率出现在坐标轴上,因此每一维的参数都不会是 0。
采用 L2 正则化优化手写数字神经网络
我们使用深度学习框架Pytorch搭建神经网络并使用L2正则化技术,完成对手写数字数据集mnist的拟合和预测。
在此之前需要先介绍一下mnist数据集,该数据分为训练集和测试集两部分,训练集由60000张灰色图像组成,每张图像大小为28*28,标签共有10类(0-9),分别代表该图片所代表的数字。如下图灰色图像,其标签为0。

测试集共有10000张灰色图像,格式与训练集相同。
我们首先不使用L2正则化运行,再和使用L2正则化的情况对比,从而更直观地感受不同。
根据我们的需要,我们首先导入以下库,方便后续程序调用:
import torch
import torchvision
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader
接下来,我们设置一下模型训练需要的超参数:
batch_size_train = 64
batch_size_test = 1000
learning_rate = 0.01
log_interval = 10
random_seed = 1
torch.manual_seed(random_seed)
其中:
batch_size_train:训练时的batch大小;
batch_size_test:测试时的batch大小;
learning_rate;学习率大小;
log_interval:每多少batch打印损失;
random_seed:随机种子,保证实验中不受随机性影响。
然后导入与制作数据集:
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('./data/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('./data/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_test, shuffle=True)
通过上面的代码,我们分别获取了训练数据集 train_loader 与测试数据集 test_loader。
接下来搭建神经网络,我们共使用5个隐藏层,每个隐藏层的单元个数为700,输入层和输出层的维度分别为784和10,中间层的激活函数均使用relu函数,输出层激活函数选用softmax函数,原始损失函数选用多类别交叉损失函数,优化方法选用adam,评价指标选用acc:
搭建神经网络
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(784, 700)
self.fc2 = nn.Linear(700, 700)
self.fc3 = nn.Linear(700, 700)
self.fc4 = nn.Linear(700, 700)
self.fc5 = nn.Linear(700, 700)
self.fc6 = nn.Linear(700, 700)
self.fc7 = nn.Linear(700, 10)
def forward(self, x):
x = x.view(-1, 784)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.relu(self.fc4(x))
x = F.relu(self.fc5(x))
x = F.relu(self.fc6(x))
x = self.fc7(x)
return F.log_softmax(x)
然后初始化网络,并设置adam优化器:
参数设置
network = Net()
optimizer = optim.Adam(network.parameters(), lr=learning_rate)
定义迭代训练函数train:
def train(epoch):
network.train()
for batch_idx, (data, target) in enumerate(train_loader):
data = data
target = target
optimizer.zero_grad()
output = network(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
定义测试函数test:
def test():
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data = data
target = target
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
最后调用训练与测试函数:
train(1)
test()
最终测试运行结果如下:
Test set: Avg. loss: 0.4081, Accuracy: 8801/10000 (88%)
而加入L2正则化的步骤非常简单,只需要在adam优化器中设置L2正则化系数即可,这里设置的系数为0.002:
optimizer = optim.Adam(network.parameters(), lr=learning_rate, weight_decay=0.002)
同样迭代次数后运行结果如下:
Test set: Avg. loss: 0.3878, Accuracy: 9095/10000 (91%)
可以看到在测试集上的精度从88%提高到了91%,说明了正则化的加入提高了模型的泛化能力。
编程要求
本关的任务需要补全文件中 Begin-End 中间的代码,实现L2正则化技术来解决过拟合问题,提高验证集上的准确率,具体分为如下几个部分:
我的垃圾代码
import warnings
warnings.filterwarnings("ignore")
import torch
import torchvision
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader
batch_size_train = 64
batch_size_test = 1000
learning_rate = 0.01
log_interval = 10
random_seed = 1
torch.manual_seed(random_seed)
#**********begin**********#
# 导入数据
# 数据路径:/data/workspace/myshixun/data/
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/data/workspace/myshixun/data/', train=True,download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/data/workspace/myshixun/data/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_test, shuffle=True)
# 搭建神经网络
# 搭建神经网络
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(784, 700)
self.fc2 = nn.Linear(700, 700)
self.fc3 = nn.Linear(700, 700)
self.fc4 = nn.Linear(700, 700)
self.fc5 = nn.Linear(700, 700)
self.fc6 = nn.Linear(700, 700)
self.fc7 = nn.Linear(700, 10)
def forward(self, x):
x = x.view(-1, 784)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.relu(self.fc4(x))
x = F.relu(self.fc5(x))
x = F.relu(self.fc6(x))
x = self.fc7(x)
return F.log_softmax(x)
# 创建网络与优化器设置
network = Net()
optimizer = optim.Adam(network.parameters(), lr=learning_rate, weight_decay=0.002)
#**********end**********#
# 训练函数
def train(epoch):
network.train()
for batch_idx, (data, target) in enumerate(train_loader):
data = data
target = target
optimizer.zero_grad()
output = network(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
epoch, batch_idx * len(data), len(train_loader.dataset),
100. * batch_idx / len(train_loader), loss.item()))
# 测试函数
def test():
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data = data
target = target
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
return 100 * float(correct) / float(len(test_loader.dataset))
train(1)
第10关:手写数字识别之搭建向前传播过程
为了完成本关任务,你需要掌握:向前传播过程的原理和实现步骤。
搭建向前传播过程
向前传播简介
前向传播是从神经网络的输入层开始,逐渐往输出层进行前向传播,上一层的神经元与本层的神经元有连接,那么本层的神经元的激活等于上一层神经元对应的权值进行加权和运算,最后通过一个非线性函数(激活函数)如ReLu,Sigmoid等函数,最后得到的结果就是本层神经元的输出。神经网络逐层逐神经元通过该操作向前传播,最终得到输出层的结果。
计算神经网络的前向传播结果需要三部分信息:

定义激活函数和损失函数
非线性的激活函数处理非线性假设,常用的激活函数有relu、sigmoid。
代码示例:
def sigmoid(x):
return 1/(1+np.exp(-x))
def relu(x):
return np.maximum(0,x)
案例中我们使用交叉熵损失函数,代码示例:
#交叉熵损失函数
def cross_entropy(y, y_predict):
y_predict = np.clip(y_predict,1e-10,1-1e-10) #防止0*log(0)出现。导致计算结果变为NaN
return -(y * np.log(y_predict) + (1 - y) * np.log(1 - y_predict))
搭建向前传播过程的神经网络
代码示例:
class Network:
def __init__(self,inputnodes,hidnodes,outputnodes,learning_rate):
self.innodes = inputnodes
self.hidnodes = hidnodes
self.outnodes = outputnodes
self.lr = learning_rate
#各层权重 偏置
self.W1 = np.random.randn(self.hidnodes, self.innodes) * 0.01
self.W2 = np.random.randn(self.outnodes, self.hidnodes) * 0.01
self.b1 = np.random.randn(self.hidnodes, 1) * 0.01
self.b2 = np.random.randn(self.outnodes, 1) * 0.01
def predict(self,X):
# 前向传播算法forward_propagation,实现预测
self.a1 = X.T
self.z2 = np.dot(self.W1,self.a1)+self.b1
self.a2 = relu(self.z2)
self.z3 = np.dot(self.W2,self.a2)+self.b2
self.a3 = relu(self.z3)
out = self.a3
p = np.argmax(out, axis=0) # 输出层的最大索引下标即为标签值,标签值0-9
return p
def backward(self, dAL):
m=60000
dZ3=np.multiply(dAL,relu_derivative(self.z3))
dW2=np.dot(dZ3, self.a2.T)/m
db2=np.mean(dZ3,axis=1)
dAL_1 = np.dot(self.W2.T, dZ3)
dZ2 = np.multiply(dAL_1, relu_derivative(self.z2))
dW1 = np.dot(dZ2, self.a1.T) / m
db1 = np.mean(dZ2, axis=1)
# 梯度下降
self.W2-=self.lr*dW2
self.b2-=self.lr*db2
self.W1 -= self.lr * dW1
self.b1 -= self.lr * db1
我的垃圾代码
import numpy as np
#交叉熵损失函数
def cross_entropy(y, y_predict):
y_predict = np.clip(y_predict,1e-10,1-1e-10)
return -(y * np.log(y_predict) + (1 - y) * np.log(1 - y_predict))
#交叉熵损失函数的导函数
def cross_entropy_der(y,y_predict):
return -y/y_predict+(1-y)/(1-y_predict)
def sigmoid(x):
return 1/(1+np.exp(-x))
def relu(x):
return np.maximum(0,x)
def sig_derivative(x):
#sig函数求导
fx=sigmoid(x)
return fx*(1-fx)
def relu_derivative(x):
return (x>=0).astype(np.float64)
class Network:
def __init__(self,inputnodes,hidnodes,outputnodes,learning_rate):
self.innodes = inputnodes
self.hidnodes = hidnodes
self.outnodes = outputnodes
self.lr = learning_rate
#各层权重 偏置
self.W1 = np.random.randn(self.hidnodes, self.innodes) * 0.01
self.W2 = np.random.randn(self.outnodes, self.hidnodes) * 0.01
self.b1 = np.random.randn(self.hidnodes, 1) * 0.01
self.b2 = np.random.randn(self.outnodes, 1) * 0.01
def predict(self,X):
# 任务:补充代码,完成搭建向前传播过程
########## Begin ##########
self.a1 = X.T
self.z2 = np.dot(self.W1,self.a1)+self.b1
self.a2 = relu(self.z2)
self.z3 = np.dot(self.W2,self.a2)+self.b2
self.a3 = relu(self.z3)
out = self.a3
p = np.argmax(out, axis=0) # 输出层的最大索引下标即为标签值,标签值0-9
return p
######### End ##########
def backward(self, dAL):
m=60000
dZ3=np.multiply(dAL,relu_derivative(self.z3))
dW2=np.dot(dZ3, self.a2.T)/m
db2=np.mean(dZ3,axis=1)
dAL_1 = np.dot(self.W2.T, dZ3)
dZ2 = np.multiply(dAL_1, relu_derivative(self.z2))
dW1 = np.dot(dZ2, self.a1.T) / m
db1 = np.mean(dZ2, axis=1)
# 梯度下降
self.W2-=self.lr*dW2
self.b2-=self.lr*db2
self.W1 -= self.lr * dW1
self.b1 -= self.lr * db1
第11关:测试集
为了完成本关任务,你需要掌握:
1.训练集、验证集和测试集的概念以及相应的作用。
2.划分一个简单的数据集。
训练集、测试集与验证集
在模式识别(pattern recognition)与机器学习(machine learning)的相关研究中,数据集的划分时常影响我们的准确率,好的数据集划分一般分为训练集(training set),验证集(validation set)和测试集(test set)。在有些机器学习算法中,数据集往往也被拆分为两份:训练集和测试集。
训练集:
用于模型拟合的数据样本,即用于训练的样本集合,主要用来训练神经网络中的参数,我们的模型在训练集上进行学习,通常在这个阶段我们可以有多种方法进行训练。其作用是:拟合模型,调整网络权重。
验证集:
模型训练过程中单独留出的样本集,它可以用于调整模型的超参数和用于对模型的能力进行初步评估。可以挑选最优模型超参的样本集合:使用验证集可以得到反向传播什么时候结束以及超参怎么设置最合理。主要作用是为了挑选在验证集上表现最好的模型。由于此关卡未涉及到模型的验证,因此下面将忽略验证集的设定,只使用训练集和测试集。
测试集:
用来评估模最终模型的泛化能力,但不能作为调参、选择特征等算法相关的选择的依据。 为了测试已经训练好的模型的精确度。因为在训练模型的时候,参数全是根据现有训练集里的数据进行修正、拟合,有可能会出现过拟合的情况,即这个参数仅对训练集里的数据拟合比较准确,如果出现一个新数据需要利用模型预测结果,准确率可能就会很差。
测试集的作用
测试集的作用是为了对学习器的泛化误差进行评估,即进行实验测试以判别学习器对新样本的判别能力,同时以测试集的的测试误差”作为泛化误差的近似。因此在分配训练集和测试集的时候,如果测试集的数据越小,对模型的泛化误差的估计将会越不准确。所以需要在划分数据集的时候进行权衡。
测试集的比例
训练集数据的数量一般占2/3到4/5。在实际应用中,基于整个数据集数据的大小,训练集数据和测试集数据的划分比例可以是6:4、7:3或8:2。对于庞大的数据可以使用9:1,甚至是99:1。具体根据测试集的划分方法有所不同。
划分简单的数据
自定义一个划分训练集和测试集的函数:
def train_test_split(dataset, train=0.6):
"""
该函数用于划分训练集和测试集
Parameters
----------
dataset : 二维列表
传入需要划分成训练集和测试集的数据集.
train : 浮点数
传入训练集占整个数据集的比例.默认是0.6.
Returns
-------
train_basket : 二维列表
划分好的训练集.
dataset_copy : 二维列表
划分好的测试集.
"""
# 创建一个空列表用于存放后面划分好的训练集
train_basket = list()
# 根据输入的训练集的比例计算出训练集的大小(样本数量)
train_size = train * len(dataset)
# 复制出一个新的数据集来做切分,从而不改变原始的数据集
dataset_copy = list(dataset)
# 执行循环判断,如果训练集的大小小于所占的比例,就一直往训练集里添加数据
while len(train_basket) < train_size:
# 通过randrange()函数随机产生训练集的索引
random_choose = randrange(len(dataset_copy))
# 根据上面生成的训练集的索引将数据集中的样本加到train_basket中
# 注意pop函数会根据索引将数据集中的样本给移除,所以循环结束之后剩下的样本就是测试集
train_basket.append(dataset_copy.pop(random_choose))
return train_basket, dataset_copy
我的垃圾代码
# 导入库
from random import seed # 用于固定每次生成的随机数都是确定的(伪随机数)
from random import randrange # 用于生成随机数
def train_test_split(dataset, train=0.6):
# 创建一个空列表用于存放后面划分好的训练集
train_basket = list()
# 根据输入的训练集的比例计算出训练集的大小(样本数量)
train_size = train * len(dataset)
# 复制出一个新的数据集来做切分,从而不改变原始的数据集
dataset_copy = list(dataset)
# 执行循环判断,如果训练集的大小小于所占的比例,就一直往训练集里添加数据
while len(train_basket) < train_size:
########## Begin ##########
# 通过randrange()函数随机产生训练集的索引
random_choose = randrange(len(dataset_copy))
########## End ##########
########## Begin ##########
# 根据上面生成的训练集的索引将数据集中的样本加到train_basket中,注意pop函数会根据索引将数据集中的样本给移除,所以循环结束之后剩下的样本就是测试集
train_basket.append(dataset_copy.pop(random_choose))
########## End ##########
return train_basket, dataset_copy
# 主函数
if '__main__' == __name__:
# 定义一个随机种子,使得每次生成的随机数都是确定的(伪随机数)
seed(666)
dataset = [[1], [2], [3], [4], [5], [6], [7], [8], [9], [10]]
train_data,test_data = train_test_split(dataset,train = 0.8)
print("划分后的训练集数据为:",train_data,"划分后的训练集数据为:",test_data)
# 调用手动编写的train_test_split函数划分训练集和测试集
第12关:手写数字识别之数据读取及预处理
为了完成本关任务,你需要掌握:手写数字识别案例中数据读取及预处理的方法和步骤。
数据读取
在本实验中,我们使用 MNIST 数据集,MNIST数据集是NIST(National Institute of Standards and Technology,美国国家标准与技术研究所)数据集的一个子集,MNIST 数据集可在 http://yann.lecun.com/exdb/mnist/ 获取。该训练集中一共包含了 60000 张图像和标签,而测试集一共包含了 10000 张图像和标签。每张图片是一个28*28像素点的0 ~ 9的灰质手写数字图片,黑底白字,图像像素值为0 ~ 255,越大该点越白。
代码示例:
def train_labels_ana(filepath):
"""解析特征数据集 .idx1-ubyte格式"""
# 以二进制格式处理文件
with open(filepath,'rb') as fbj:
bin_data=fbj.read()
offset=0
magic_num,items_num=struct.unpack_from('>ii',bin_data,offset)
offset+=struct.calcsize('>ii')
fmt_label='>'+str(items_num)+'B'
labels=struct.unpack_from(fmt_label,bin_data,offset)
label=np.reshape(labels,[items_num])
return label
数据预处理
首先,我们需要对x数据进行归一化处理,原来x的每个像素值在[0,255]之间,现在转变成[0,1]之间。刚导入的y数据的shape是[6000],一维,存放分类数,为了和最后的预测结果比较,对它one-hot编码,shape变为[6000,10]。存放每张图属于每一个分类的概率。
代码示例:
(x, y), _ = tf.keras.datasets.mnist.load_data()
# 转换成tensor类型,x数据类型一般为float32,y存放的是图片属于哪种具体类型,属于整型
x = tf.convert_to_tensor(x, dtype=tf.float32)
y = tf.convert_to_tensor(y, dtype=tf.int32)
# 查看数据内容
print('shape:', x.shape, y.shape, '\ndtype:', x.dtype, y.dtype) # 查看shape和数据类型
print('x的最小值:', tf.reduce_min(x), '\nx的最大值:', tf.reduce_max(x)) # 查看x的数据范围
print('y的最小值:', tf.reduce_min(y), '\ny的最大值:', tf.reduce_max(y)) # 查看y的数据范围
# 预处理
x = x / 255. # 归一化处理,将x数据的范围从[0,255]变成[0,1]
y = tf.one_hot(y, depth=10) # y是分类数值,对它进行one-hot编码,shape变为[b,10]
我的垃圾代码
import numpy as np
import tensorflow as tf
from tensorflow import keras
from keras import datasets
import os
import matplotlib.pyplot as plt
import struct
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
file1="/data/workspace/myshixun/src/step1/train-images.idx3-ubyte"
file2="/data/workspace/myshixun/src/step1/train-labels.idx1-ubyte"
def train_images_ana(filepath):
"""解析图片数据集 .idx3-ubyte格式"""
# 以二进制方式读取文件
with open(filepath,'rb') as fbj:
bin_data=fbj.read()
offset=0
magic_num,image_num,rows_num,column_num=struct.unpack_from('>iiii',bin_data,offset)
offset+=struct.calcsize('>iiii')
imgsize=image_num*rows_num*column_num
fmt_image='>'+str(imgsize)+'B' # 训练集数据有60000*28*28
# 任务:补充代码,完成对图片数据集的解析
########## Begin ##########
imgs = struct.unpack_from(fmt_image, bin_data, offset)
img = np.reshape(imgs, (image_num, rows_num*column_num))
########## End ##########
return img
def train_labels_ana(filepath):
"""解析特征数据集 .idx1-ubyte格式"""
# 以二进制格式处理文件
with open(filepath,'rb') as fbj:
bin_data=fbj.read()
offset=0
magic_num,items_num=struct.unpack_from('>ii',bin_data,offset)
offset+=struct.calcsize('>ii')
fmt_label='>'+str(items_num)+'B'
labels=struct.unpack_from(fmt_label,bin_data,offset)
label=np.reshape(labels,[items_num])
return label
labels = train_labels_ana(file2)
print(labels)
imgs = train_images_ana(file1)
print(np.shape(imgs[1]))
第13关:正则化集合
相关知识
为了完成本关任务,你需要掌握:1.Dropout,2.数据增强,3.提前终止。
Dropout
什么是Dropout
L2正则化是通过修改代价函数来实现的,而Dropout则是通过修改神经网络本身来实现的,它是在训练网络时用的一种技巧。
假设我们要训练下面的这个神经网络:
在训练开始时,我们随机地删除一半的隐层单元,视它们为不存在,得到如下的网络:
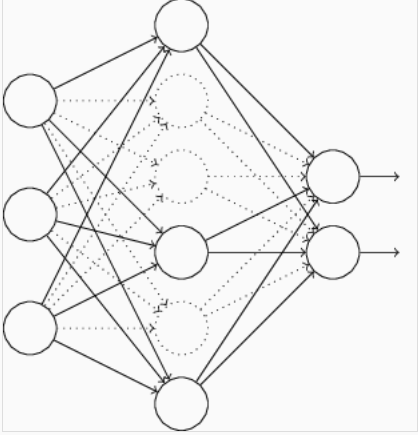
保持输入输出层不变,按照BP算法更新上图神经网络中的权值(虚线连接的单元不更新)。
以上就是一次迭代的过程,在第二次迭代中,也用同样的方法,只不过这次删除的那一半隐层单元,跟上一次删除掉的可能是不一样的,因为我们每一次迭代都是“随机”地去删掉一半。第三次、第四次……都是这样,直至训练结束。
最后,对于我们得到的参数需要根据我们每次训练的神经元的比例乘以一个一个系数,如举例中我们每次训练了50%的神经元,则所有的参数需要乘以0.5,若每次有70%的神经元参与训练,则所有的参数乘以0.7,依次类推得到最后的参数。
为什么可以防止过拟合
首先,运用了Dropout的训练过程,相当于训练了很多个只有半数隐层单元的神经网络(后面简称为“半数网络”),每一个这样的半数网络,都可以给出一个分类结果,这些结果有的是正确的,有的是错误的。随着训练的进行,大部分半数网络都可以给出正确的分类结果,那么少数的错误分类结果就不会对最终结果造成大的影响。
其次,减少神经元之间复杂的共适应关系: 因为Dropout程序导致两个神经元不一定每次都在一个Dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用,阻止了某些特征仅仅在其它特定特征下才有效果的情况。迫使网络去学习更加鲁棒的特征。
Pytorch实现
此前数据预处理和绝大多数神经网络设置的部分都和上一关卡中所提到的方法完全相同,在此不再赘述。
我们需要在网络的构造函数中添加nn.Dropout()定义,并在最后两层全连接层中添加Dropout,添加代码如下:
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(784, 1000)
self.fc2 = nn.Linear(1000, 1000)
self.fc3 = nn.Linear(1000, 1000)
self.fc4 = nn.Linear(1000, 1000)
self.fc5 = nn.Linear(1000, 1000)
self.fc6 = nn.Linear(1000, 1000)
self.fc7 = nn.Linear(1000, 10)
self.dropout = nn.Dropout(p=0.1)
def forward(self, x):
x = x.view(-1, 784)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.relu(self.fc4(x))
x = F.relu(self.dropout(self.fc5(x)))
x = F.relu(self.dropout(self.fc6(x)))
x = self.fc7(x)
return F.log_softmax(x)
其中nn.Dropout(p=0.1)中的p=0.1表示神经元有百分之10的概率被屏蔽,p的值可以根据过拟合情况自己设定。
使用Dropout的迭代后的测试结果如下:
Test set: Avg. loss: 0.3748, Accuracy: 9123/10000 (91%)
可以看到相比于直接搭建神经网络,在验证集上的精度从86%提高到了91%,说明该方法是可以解决过拟合的问题,从而得到更好的泛化能力。
数据增强
什么是数据增强
数据增强是通过一定的规则扩充数据集,得到更多的数据。
以图片数据集举例,可以做各种变换,如:
将原始图片旋转一个小角度;
添加随机噪声;
一些有弹性的畸变;
截取原始图片的一部分。
为什么可以防止过拟合
由于浅层的神经网络有的时候很难拟合出数据的分布,在实际中,我们通常会增加神经网络的深度和广度,从而让神经网络的学习能力增强,便于拟合训练数据的分布情况。
然而随着神经网络的加深,需要学习的参数也会随之增加,这样就会更容易导致过拟合,当数据集较小的时候,过多的参数会拟合数据集的所有特点,而非数据之间的共性。而数据增强的合理运用,可以帮助我们增加数据集的大小,从而在神经网络加深的时候,依然拟合出较为合理的数据分布。
Pytorch实现该技术
此前数据预处理和绝大多数神经网络设置的部分都和上一关卡中所提到的方法完全相同,在此不再赘述,但是为了使用数据增强,我们需要在训练数据集的加载中添加torchvision库中的数据增强操作torchvision.transforms.RandomRotation(20)为我们的训练图片随机旋转-20°到20°。
代码如下:
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('./data/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.RandomRotation(20),
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True)
而测试数据集加载我们不需要做任何更改。
同样的训练最终得到的结果如下:
Test set: Avg. loss: 0.5018, Accuracy: 8906/10000 (89%)
可以看到在验证集上的精度从原来的88%提高到了89%,说明该方法可以解决过拟合的问题,提高模型的泛化能力。
提前终止
什么是提前终止
提前停止就是在验证误差开始上升之前,就把网络的训练停止了,具体做法是每次在给定的迭代次数K内,把出现比之前验证误差更小的参数(模型)记录下来。如果从上次记录最小值开始,迭代了K次仍然没有发现新的更小的验证误差,那就认为已经过拟合,把当前验证误差最小的模型当做最优模型。
为什么可以防止过拟合
神经网络的优化算法可以使模型对训练集的拟合效果不断优化,但是到了一定的程度以后,我们所拟合的是训练数据中所含有的噪音,从而导致随着训练次数的增多,在验证集上的效果反而变差的情况,如下图所示:
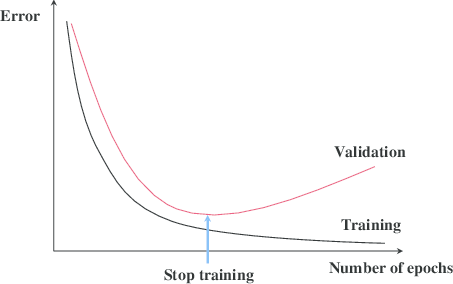
所以我们使用提前终止技术,在多轮验证集效果都没有提升的情况下停止训练,避免将训练集中的噪声数据误认为是数据的真实分布而拟合到模型中,从而可以避免过拟合的出现,提升模型的泛化能力。
Pytorch实现
此前数据预处理和绝大多数神经网络设置的部分都和上一关卡中所提到的方法完全相同,在此不再赘述,这里在训练过程中,我们首先训练30个epoch不提前终止,让其达到一个过拟合的状态:
acc = 0
for epoch in range(1, 30):
train(epoch)
acc = test()
acc用来记录测试集的精度。
训练30个epoch以后得到结果如下:
Test set: Avg. loss: 0.5489, Accuracy: 8270/10000 (82%)
可以看到测试集精度只有82%,出现了明显的过拟合现象。
接下来我们定义提前终止的判断类:
class EarlyStopping(object):
def __init__(self, monitor: str = 'val_loss', mode: str = 'min', patience: int = 1):
"""
:param monitor: 要监测的指标,只有传入指标字典才会生效
:param mode: 监测指标的模式,min 或 max
:param patience: 最大容忍次数
"""
self.monitor = monitor
self.mode = mode
self.patience = patience
self.__value = -math.inf if mode == 'max' else math.inf
self.__times = 0
def state_dict(self) -> dict:
""":保存状态,以便下次加载恢复
torch.save(state_dict, path)
"""
return {
'monitor': self.monitor,
'mode': self.mode,
'patience': self.patience,
'value': self.__value,
'times': self.__times
}
def load_state_dict(self, state_dict: dict):
""":加载状态
:param state_dict: 保存的状态
"""
self.monitor = state_dict['monitor']
self.mode = state_dict['mode']
self.patience = state_dict['patience']
self.__value = state_dict['value']
self.__times = state_dict['times']
def reset(self):
""":重置次数
"""
self.__times = 0
def __call__(self, metrics) -> bool:
"""
:param metrics: 指标字典或数值标量
:return: 返回bool标量,True表示触发终止条件
"""
if isinstance(metrics, dict):
metrics = metrics[self.monitor]
if (self.mode == 'min' and metrics <= self.__value) or (
self.mode == 'max' and metrics >= self.__value):
self.__value = metrics
self.__times = 0
else:
self.__times += 1
if self.__times >= self.patience:
return True
return False
重新添加提前终止训练网络:
# 初始化,监测模式为最大,最多容忍3次
early_stop = EarlyStopping(mode='max', patience=3)
acc = 0
for epoch in range(1, 30):
train(epoch)
acc = test()
if early_stop(acc):
break
训练以后得到结果如下:
Test set: Avg. loss: 0.3297, Accuracy: 9216/10000 (92%)
可以看到相比于直接搭建神经网络,在验证集上的精度从82%提高到了92%,说明该方法是可以解决过拟合的问题,从而得到更好的泛化能力。
我的垃圾代码
import warnings
warnings.filterwarnings("ignore")
import torch
import torchvision
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.utils.data import DataLoader
import math
batch_size_train = 64
batch_size_test = 1000
learning_rate = 0.01
log_interval = 10
random_seed = 1
torch.manual_seed(random_seed)
# 导入数据
# 数据路径:/data/workspace/myshixun/data/
train_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/data/workspace/myshixun/data/', train=True, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_train, shuffle=True)
test_loader = torch.utils.data.DataLoader(
torchvision.datasets.MNIST('/data/workspace/myshixun/data/', train=False, download=True,
transform=torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize(
(0.1307,), (0.3081,))
])),
batch_size=batch_size_test, shuffle=True)
# 搭建神经网络
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.fc1 = nn.Linear(784, 700)
self.fc2 = nn.Linear(700, 700)
self.fc3 = nn.Linear(700, 700)
self.fc4 = nn.Linear(700, 700)
self.fc5 = nn.Linear(700, 700)
self.fc6 = nn.Linear(700, 700)
self.fc7 = nn.Linear(700, 10)
def forward(self, x):
x = x.view(-1, 784)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.relu(self.fc4(x))
x = F.relu(self.fc5(x))
x = F.relu(self.fc6(x))
x = self.fc7(x)
return F.log_softmax(x)
# 创建网络与优化器设置
network = Net()
optimizer = optim.Adam(network.parameters(), lr=learning_rate)
# 训练函数
def train(epoch):
network.train()
for batch_idx, (data, target) in enumerate(train_loader):
data = data
target = target
optimizer.zero_grad()
output = network(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
# if batch_idx % log_interval == 0:
# print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
# epoch, batch_idx * len(data), len(train_loader.dataset),
# 100. * batch_idx / len(train_loader), loss.item()))
# 测试函数
def test():
network.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data = data
target = target
output = network(data)
test_loss += F.nll_loss(output, target, size_average=False).item()
pred = output.data.max(1, keepdim=True)[1]
correct += pred.eq(target.data.view_as(pred)).sum()
test_loss /= len(test_loader.dataset)
print('\nTest set: Avg. loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
return 100 * float(correct) / float(len(test_loader.dataset))
#**********begin**********#
# 提前终止类
class EarlyStopping(object):
def __init__(self, monitor: str = 'val_loss', mode: str = 'min', patience: int = 1):
"""
:param monitor: 要监测的指标,只有传入指标字典才会生效
:param mode: 监测指标的模式,min 或 max
:param patience: 最大容忍次数
"""
self.monitor = monitor
self.mode = mode
self.patience = patience
self.__value = -math.inf if mode == 'max' else math.inf
self.__times = 0
def state_dict(self) -> dict:
""":保存状态,以便下次加载恢复
torch.save(state_dict, path)
"""
return {
'monitor': self.monitor,
'mode': self.mode,
'patience': self.patience,
'value': self.__value,
'times': self.__times
}
def load_state_dict(self, state_dict: dict):
""":加载状态
:param state_dict: 保存的状态
"""
self.monitor = state_dict['monitor']
self.mode = state_dict['mode']
self.patience = state_dict['patience']
self.__value = state_dict['value']
self.__times = state_dict['times']
def reset(self):
""":重置次数
"""
self.__times = 1
def __call__(self, metrics) -> bool:
"""
:param metrics: 指标字典或数值标量
:return: 返回bool标量,True表示触发终止条件
"""
if isinstance(metrics, dict):
metrics = metrics[self.monitor]
if (self.mode == 'min' and metrics <= self.__value) or (
self.mode == 'max' and metrics >= self.__value):
self.__value = metrics
self.__times = 0
else:
self.__times += 1
if self.__times >= self.patience:
return True
return False
#**********end**********#
#**********begin**********#
# 初始化提前终止对象,监测模式为最大,最多容忍3次
# 初始化,监测模式为最大,最多容忍3次
early_stop = EarlyStopping(mode='max', patience=3)
#**********end**********#