图

大部分定义都在离散数学II中学过了，所以对于已知或常见的我不多赘述

• 弧或边带权的图分别称作有向网或无向网。
• 若边或弧的个数 e<nlogn，则称作稀疏图，否则称作稠密图。
• 对有向图，若任意两个顶点之间都存在一条有向路径，则称此有向图为强连通图。

基本操作

• CreatGraph(&G, V, VR):
  // 按定义(V, VR) 构造图
• DestroyGraph(&G):
  // 销毁图
• LocateVex(G, u);
  // 若G中存在顶点u，则返回该顶点在图中“位置” ；否则返回其它信息。
• GetVex(G, v); // 返回 v 的值。
• PutVex(&G, v, value);
  // 对 v 赋值value。
• FirstAdjVex(G, v);
  // 返回 v 的“第一个邻接点” 。若该顶点在 G 中没有邻接点，则返回“空”。
• NextAdjVex(G, v, w);
  // 返回 v 的（相对于 w 的） “下一个邻接点”。若 w 是 v 的最后一个邻接点，则返回“空”。
• InsertVex(&G, v);
  //在图G中增添新顶点v。
• DeleteVex(&G, v);
  // 删除G中顶点v及其相关的弧。
• InsertArc(&G, v, w);
  // 在G中增添弧<v,w>，若G是无向的，则还增添对称弧<w,v>。
• DeleteArc(&G, v, w);
  //在G中删除弧<v,w>，若G是无向的，则还删除对称弧<w,v>。
• DFSTraverse(G, v, Visit());
  //从顶点v起深度优先遍历图G，并对每个顶点调用函数Visit一次且仅一次。
• BFSTraverse(G, v, Visit());
  //从顶点v起广度优先遍历图G，并对每个顶点调用函数Visit一次且仅一次。

存储结构

邻接矩阵：

typedef struct {
    char* vexs[MAX_VERTEX_NUM]; // 顶点列表，每个元素为一个字符串，代表一个顶点
    ArcCell arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵，二维数组表示从一个顶点到另一个顶点的弧，每个弧存储了该弧的相关信息
    int vexnum; // 顶点个数
    int arcnum; // 弧个数
    GraphKind kind; // 图的类型
} MGraph;

邻接表：

typedef struct ArcNode {
    int adjvex; // 该弧所指向的顶点的位置
    struct ArcNode* nextarc; // 指向下一条弧的指针
    char* info; // 该弧相关信息的指针
} ArcNode;

typedef struct VNode {
    char* data; // 顶点信息
    ArcNode* firstarc; // 指向第一条依附该顶点的弧
} VNode, AdjList[MAX_VERTEX_NUM];

十字链表

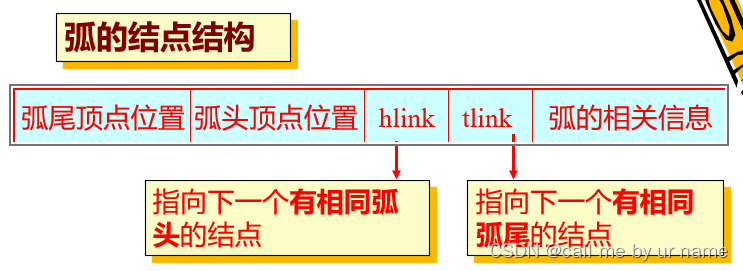
<v,w>表示从 v 到 w 的一条弧，并称 v 为弧尾，w 为弧头。

typedef struct ArcBox { // 弧的结构表示
    int tailvex, headvex; // 该弧尾和头顶点的位置
    struct ArcBox* hlink, *tlink; // 分别指向同一头结点和同一尾结点的下一条弧
    char* info; //该弧相关信息的指针
} ArcBox;
typedef struct VexNode { // 邻接多重表的结构表示
    char data; // 存储顶点信息
    ArcBox* firstin, *firstout; // 分别指向以该顶点为终点和起点的第一条弧
} VexNode;

这个应该不是很重要，主要都是邻接矩阵

遍历

深度优先搜索dfs（这个比较熟了，不过多赘述）
一种非递归写法：

void DFS(Graph G, int v) {
    int w;
    InitStack(&S); // 初始化栈S
    Push(&S, v);
    visited[v] = TRUE; // 标记起点v已访问
    while (!StackEmpty(S)) {
        Pop(&S, &v); // 取出栈顶元素v
        Visit(v); // 访问v
        w = FirstAdjVex(G, v); // 求v的第一个邻接点w
        while (w >= 0) {
            if (!visited[w]) { // w为v的尚未访问的邻接顶点
                Push(&S, w); // 将w入栈
                visited[w] = TRUE; // 标记w为已访问
            }
            w = NextAdjVex(G, v, w); // 求v相对于w的下一个邻接点
        } // end while
    } // end while
}

广度优先搜索bfs（类似 ‘树’ 那章的层次遍历）

void BFSTraverse(Graph G, Status(*Visit)(int)) {
    int v, w;
    Status status; // 初始化一个状态变量
    Queue Q; // 定义辅助队列Q
    for (v = 0; v < G.vexnum; ++v)
        visited[v] = FALSE; // 初始化访问标志
    InitQueue(&Q); // 置空的辅助队列Q
    for (v = 0; v < G.vexnum; ++v) {
        if (!visited[v]) { // v尚未访问
            visited[v] = TRUE; // 标记v为已访问
            status = Visit(v); // 访问v
            if (status == ERROR) return; // 如果访问失败，则返回错误
            EnQueue(&Q, v); // 将v入队列
            while (!QueueEmpty(Q)) { // 队列不为空时执行循环
                DeQueue(&Q, &u); // 队头元素出队并置为u
                for (w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)) {
                    if (!visited[w]) { // w为u的尚未访问的邻接顶点
                        visited[w] = TRUE; // 标记w为已访问
                        status = Visit(w); // 访问w
                        if (status == ERROR) return; // 如果访问失败，则返回错误
                        EnQueue(&Q, w); // 将w入队列
                    } // if
                } // for
            } // while
        }
    }
}

for (w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w)) 这一条代码仔细看看

最小生成树

1. 生成树：
   是一个极小连通子图，它含有图中全部顶点，但只有 n-1 条边。

2. 最小生成树：
   如果无向连通图是一个带权图，那么它的所有生成树中必有一棵边的权值总和为最小的生成树，称这棵生成树为最小代价生成树，简称最小生成树。

Kruskal算法特点：将边归并，适于求稀疏网的最小生成树。

Prime算法特点：将顶点归并，与边数无关，适于稠密网。

普里姆算法

在生成树的构造过程中，图中 n 个顶点分属两个集合：已落在生成树上的顶点集 U 和尚未落在生成树上的顶点集 V-U ，则应在所有连通 U 中顶点和 V-U 中顶点的边中选取权值最小的边。

设置一个辅助数组 closedge，对当前 V-U 集中的每个顶点，在辅助数组中存在一个相应分量 closedge[i-1]，它包括两个域，其中 lowcost 存储该边上的权。对每个顶点 vi ∈ V-U，有如下公式成立：

closedge[i-1].lowcost = Min { cost(u, v) | u ∈ U }

其中 cost(u, v) 表示边 (u, v) 的权值。显然，lowcost 记录的是当前该节点与已选择的节点中权值最小的边的权值。

struct {
    VertexType adjvex;  // U集中的顶点序号
    VRType lowcost;     // 边的权值
} closedge[MAX_VERTEX_NUM];

算法

void MiniSpanTree_P(MGraph G, VertexType u) {
    int i, j, k;
    k = LocateVex(G, u);
    for (j = 0; j < G.vexnum; ++j) {
        if (j != k) {
            closedge[j].adjvex = u;
            closedge[j].lowcost = G.arcs[k][j].adj;
        }
    }
    closedge[k].lowcost = 0;
    for (i = 1; i < G.vexnum; ++i) {
        k = minimum(closedge);  // 求出加入生成树的下一个顶点(k)
        printf("(%d, %d) ", closedge[k].adjvex, G.vexs[k]);  // 输出生成树上一条边
        closedge[k].lowcost = 0;  // 第k顶点并入U集
        for (j = 0; j < G.vexnum; ++j) { // 修改其它顶点的最小边
            if (G.arcs[k][j].adj < closedge[j].lowcost) {
                closedge[j].adjvex = G.vexs[k];
                closedge[j].lowcost = G.arcs[k][j].adj;
            }
        }
    }
}

k = minimum(closedge);
if (G.arcs[k][j].adj < closedge[j].lowcost) { closedge[j].adjvex = G.vexs[k]; closedge[j].lowcost = G.arcs[k][j].adj; }
这2条代码值得看看
时间复杂度是$O(n^2)$

克鲁斯卡尔算法

1. 构造只含 n 个顶点的子图 SG。

2. 从权值最小的边开始，如果添加这条边不会在 SG 中产生回路，则在 SG 上加上这条边。

3. 重复以上步骤，直至 SG 上加上 n-1 条边为止。

4. 再次重复以上步骤，构造另一个最小生成树。

具体参考
时间复杂度$O(eloge)$

拓扑排序、关键路径

拓扑排序

适用于有向无环图

拓扑排序是一种特殊的排序方式，它基于有向图中各个节点之间的依赖关系，通过一系列的操作得到拓扑有序序列。具体实现方式是：按照有向图给出的次序关系，将图中顶点排成一个线性序列，对于有向图中没有限定次序关系的顶点，则可以人为加上任意的次序关系。由此所得顶点的线性序列称之为拓扑有序序列。

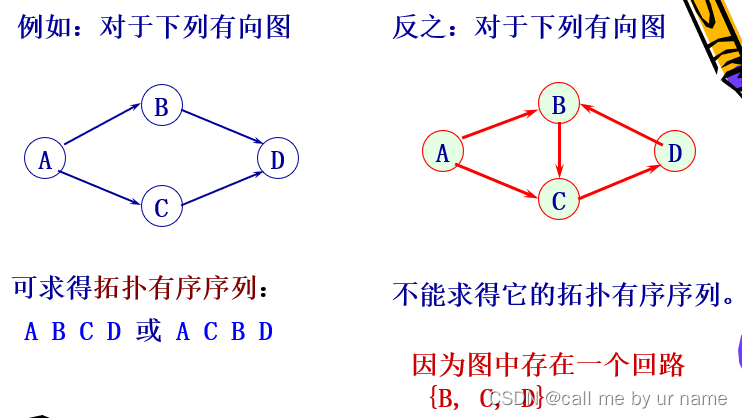
拓扑排序的实现步骤如下：

1. 从有向图中选取一个没有前驱的顶点，并输出之；
2. 从有向图中删除此顶点以及所有以它为尾的弧；
3. 重复步骤 1 和 2，直至图为空，或者图不空但找不到无前驱的顶点为止。后一种情况说明有向图中存在环。

关键路径

在关键路径的分析中，我们需要计算每个事件（顶点）的最早发生时间和最迟发生时间：

1. 事件（顶点）的最早发生时间 ve(j) 等于从源点到顶点 Vj 的最长路径长度；
   这个时间决定了所有以 Vj 为尾的弧所表示的活动的最早开始时间。

2. 事件（顶点）的最迟发生时间 vl(k) 表示在不推迟整个工程完成的前提下，事件最迟发生的时间；
   vl(k) 等于工程完成时间减去从顶点 Vk 到汇点的最长路径长度。

在关键路径分析中，计算事件发生时间的公式如下：

事件发生时间的计算公式：

- ve(源点) = 0；
- ve(k) = Max {ve(j) + dut(<j, k>)}

   其中，dut(<j,k>) 表示从顶点 j 到顶点 k 的活动所需的时间或耗费。

- vl(汇点) = ve(汇点)；
- vl(j) = Min {vl(k) - dut(<j, k>)}

   其中，vl(j) 表示从顶点 j 开始到工程结束所能容忍的最大延迟时间。

在关键路径分析中，求解最早发生时间 ve 和最迟发生时间 vl 的顺序如下：

1. 求 ve 顺序：按拓扑有序的次序，从源点开始，依次计算每个顶点的最早发生时间。

2. 求 vl 顺序：按拓扑逆序的次序，从汇点开始，依次计算每个顶点的最迟发生时间。

最短路径

1. 单源最短路径算法 - Dijkstra（迪杰斯特拉）算法：
   该算法可以求解从源点到其它所有顶点的最短路径，但要求图中不存在负权边。

2. 所有顶点间的最短路径算法 - Floyd（弗洛伊德）算法：
   该算法可以求解图中任意两个顶点之间的最短路径，可以处理带有负权边的图。

在图论中，最短路径和最短路径长度的概念如下：

1. 对于一个无权图，从一个结点到另一个结点可能存在多条路径，路径长度最短的那条路径称为最短路径。其长度称为最短路径长度。

2. 对于一个带权图，从一个结点到另一个结点可能存在多条路径，带权路径长度最短的那条路径称为最短路径。其带权路径长度称为最短路径长度。

具体参考

习题

深度优先搜索、邻接表是否存在路径

试基于图的深度优先搜索策略写一算法，判别以邻接表方式存储的有向图中是否存在由顶点$vi$到顶点$vj$的路径（$i\ne j$）注意：算法中涉及的图的基本操作必须在此存储结构上实现。

#define MAX 100
typedef struct Arc {
    int vex;
    struct Arc *next;
    int info;
} Arc;
typedef struct Vertex {
    int info;
    Arc *first;
} Vertex;
Vertex vertex[MAX]; // 图的顶点集合，最多储存 MAX 个顶点
int visited[MAX]; // 记录每个顶点是否被访问过
int DFS(int i, int j) { // 从第 i 个顶点开始，寻找是否有一条路径连接到第 j 个顶点
    Arc* p; 
    if(i == j) return 1; // 如果 i 和 j 相同，返回 1 表示有路径连接
    else {
        visited[i] = 1; // 标记 i 为已访问
        for(p = vertex[i].first; p != NULL; p = p->next) { // 遍历顶点 i 的所有邻居
            int k = p->vex; // 取出邻居的编号
            if(!visited[k] && DFS(k, j)) return 1; // 如果邻居没有被访问过且与 j 有路径连接，返回 1
        }
        return 0; // 没有找到从 i 到 j 的路径，返回 0
    }
}

仍然上一题的要求、但是广搜

#define MAX 100
typedef struct Arc {
    int vex;
    struct Arc *next;
    int info;
} Arc;
typedef struct Vertex {
    int info;
    Arc *first;
} Vertex;
Vertex vertex[MAX]; // 图的顶点集合，最多储存 MAX 个顶点
bool visited[MAX]; // 记录每个顶点是否被访问过
int BFS(int i, int j) {
    Arc* p; 
    Queue Q;
    initQueue(&Q);
    visited[i] = 1; 
    enQueue(&Q, i); 
    
    while(!isEmpty(Q)) {
        int cur = deQueue(&Q); 
        if(cur == j)  return 1;
        for(p = vertex[cur].first; p != NULL; p = p->next) {
            int k = p->vex; 
            if(!visited[k]) { 
                visited[k] = 1; 
                enQueue(&Q, k); 
            }
        }
    }
    return 0;
}

基于邻接表存储结构的Dijkstra算法

#define MAXN 100010
#define INF 0x3f3f3f3f
typedef struct Edge {
    int v; // 边的终点
    int w; // 边的权值
    int next; // 指向下一条边的指针
} Edge;
Edge edge[MAXN]; // 存储所有边的数组
int head[MAXN]; // 邻接表头指针
int dist[MAXN]; // 存储源点到各个顶点的最短距离
bool vis[MAXN]; // 标记顶点是否被访问过
// Dijkstra算法求解最短路径
void dijkstra(int s) {
    memset(vis, false, sizeof(vis));
    memset(dist, INF, sizeof(dist));
    dist[s] = 0;
    for (int k = 1; k < n; k++) { // 重复n-1次
        int u = -1;
        for (int i = 1; i <= n; i++) { // 找到一个未被访问过的距离最小的顶点u
            if (!vis[i] && (u == -1 || dist[i] < dist[u])) u = i;
        }
        vis[u] = true; // 标记u已经被访问过
        // 遍历与u相邻的所有顶点v，更新源点到v之间的最短距离
        for (int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i].v;
            int w = edge[i].w;
            if (!vis[v] && dist[u] + w < dist[v]) dist[v] = dist[u] + w;
        }
    }
}