接上一篇博客
来自ABAQUS DOCUMENT/GETTING STARTED WITH ABAQUS/CAE /USING CONTINUUM ELEMENTS
整理了典型实体单元类型的优缺点,和问题
1. 单元公式和积分
1.1 full integration —— shear lock
“完全积分”是指当单元具有规则形状时,对单元刚度矩阵中的多项式项进行精确积分所需的高斯点数。对于六面体和四边形元素,“规则形状”意味着边缘是直的,并以直角相交,任何边缘节点都位于边缘的中点。
完全积分的线性元素在每个方向上使用两个积分点。因此,三维单元C3D8在单元中使用一个2 × 2 × 2的积分点数组。完全积分的二阶单元每个方向上有3个积分点。
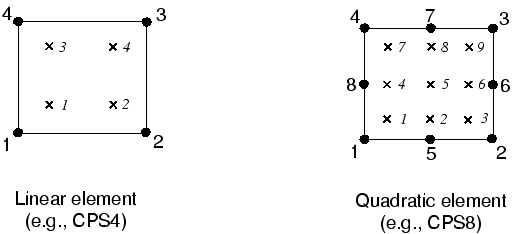
探究元素的阶数(线性与二阶)和网格密度对结果精度的影响
采用了几种不同单元和网格密度,在Abaqus/Standard模拟悬臂梁问题:
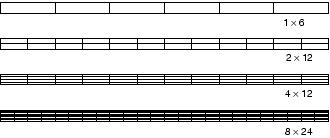
各个模拟的挠度位移与理论值3.09 mm的比值:
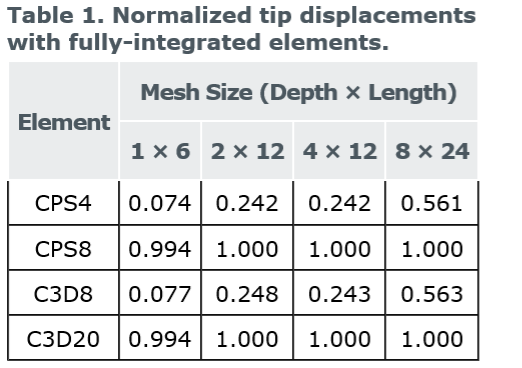
对于线性的,完全集成的单元,单元再密都不准。以上挠度模拟不准是由==剪切锁紧引起的,这是所有完全集成的一阶实体单元都存在的问题==
什么是剪切闭锁?(shear lock)
剪切锁紧会导致单元在弯曲时过于僵硬。
材料微元承受弯矩M时的变形:
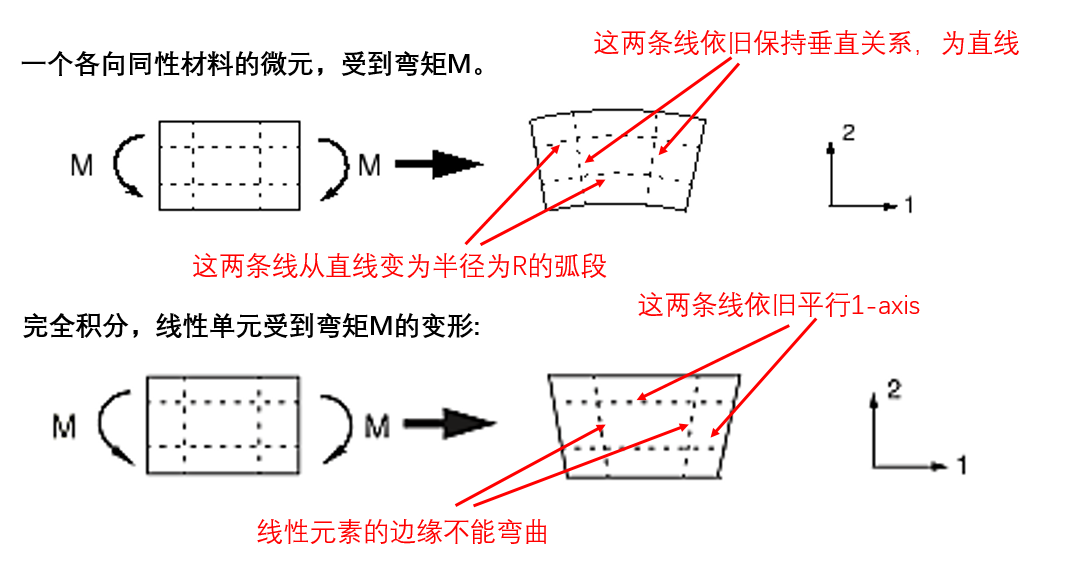
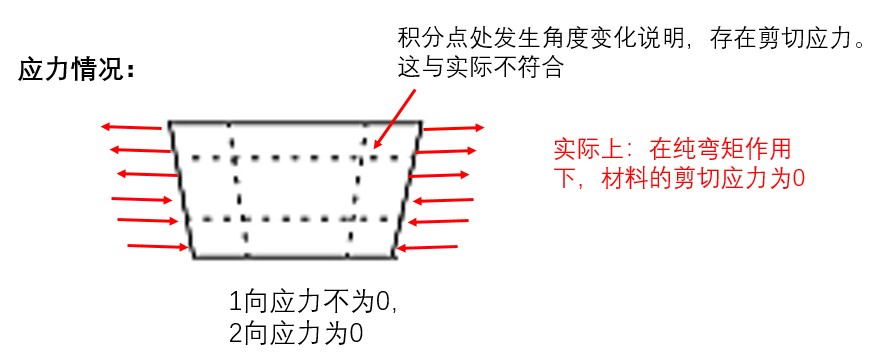
这种虚假的剪切应力产生是因为线性单元的边无法弯曲。剪切应力的存在意味着应变能产生剪切变形,而不是预期的弯曲变形,因此整体挠度较小:单元刚度太大。
剪切锁定只影响完全集成的线性元件在弯曲载荷下的性能。
对于二阶单元,剪切闭锁不是问题,因为二阶单元的边可以弯曲,但依旧有细微的剪切闭锁效应。

只有当你相当确定载荷会在模型中产生很小的弯曲时,才应该使用完全集成的线性元件。完全集成,二次元也可以锁定在复杂的应力状态。
1.2 reduced integration —— hourglassing problem
只有四边形和六面体单元可以使用缩减积分格式,其他的单元都只有full integration 格式。不过缩减积分和完全积分的单元可同时包含在一个网格
相比于完全积分,缩减积分在每个方向少一个积分点。一阶缩减积分单元只有一个积分点在质心。

同样的,采用了几种不同缩减积分单元和网格密度,在Abaqus/Standard模拟悬臂梁问题:
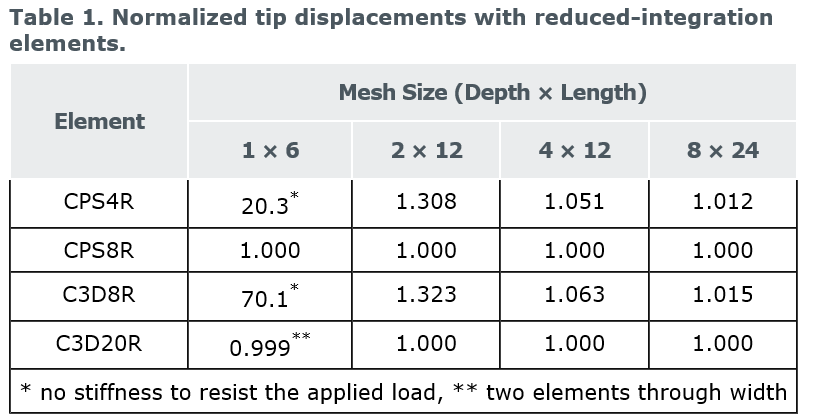
一阶缩减积分单元往往太flexible(正好和剪切闭锁的“硬”相反,这个太“软”),这个问题来自于自身的数值问题(沙漏问题/hourglassing problem)。同样地,当一个材料微元承受纯弯曲载荷时,一阶缩减积分单元变形如下:
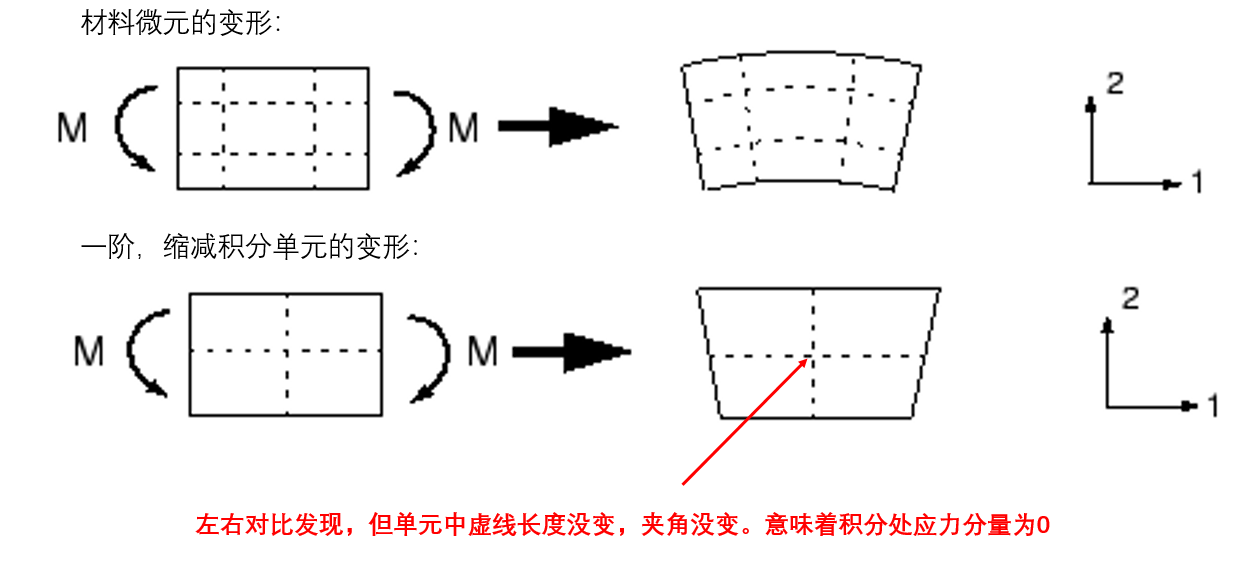
以上的单元变形是零能量模式,因为这种单元变形的应变能为0。单元无法抵抗这种变形,这意味纯弯曲刚度为0。在粗网格中,这种零能量模式通过网格传播,产生无意义的模拟结果。
针对这种情况,ABAQUS会引入少量的**沙漏刚度(hourglass stiffness)**到一阶缩减积分单元来限制沙漏模式的传播。在合理的网格密度下,沙漏刚度的引入可以有效限制沙漏问题。所以==在abaqus中只要网格足够密,一阶缩减积分单元也可以得到可接受的结果。==
正如table 2 中,厚度方向只有一个C3D8R单元时,所有积分点都在中性轴的位置上,不能抵抗弯曲载荷。对于承受弯曲载荷比较多的结构,厚度方向最好有四个以上的一阶缩减积分单元或者用二阶缩减积分单元。
ABAQUS的二阶缩减积分单元也有沙漏模式的问题。但是沙漏模式基本不可能在正常的网格里传播,而且网格足够密,沙漏模式几乎不存在。二阶单元能够应对复杂应力状态下而不存在沙漏模式。因此,二阶单元通常是大多数一般应力/位移模拟的最佳选择,除了涉及大应变的大位移模拟和某些类型的接触分析(这个是另外的原因造成的)。
1.3 Incompatible mode elements/非协调模式单元
这是一个用来解决一阶完全积分单元剪切闭锁的单元,剪切闭锁是由于单元位移场无法建模弯曲运动学而产生的。在这个单元类型中,为一阶单元引入了额外的自由度,用于加强单元变形梯度。
下图是两种单元的位移梯度变化对比(非协调单元和标准一阶单元):
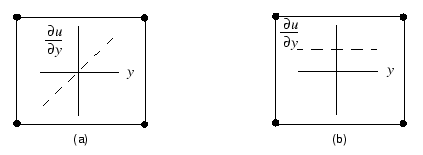
单元对变形梯度的增强完全在单元内部,而不包括节点。
abaqus 使用的公式是对于变形梯度的加强,不会导致单元间变形不协调,不会有材料干涉和空洞。
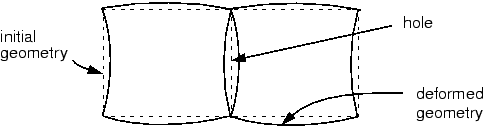
abaqus使用的formulation 更容易扩展到非线性,有限应变模拟。==对于弯曲问题,abaqus的非协调单元可得到和二阶单元相同的结果而计算成本下降。==不过,前者对单元扭曲更敏感。
下图是两种单元扭曲的模式,计算悬臂梁问题。
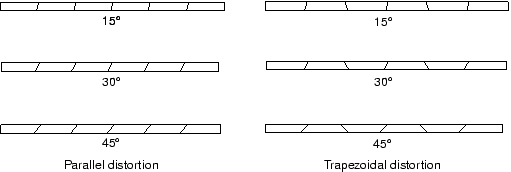
得到下图的结果,可以看到单元扭曲角度一旦大于10度,非协调单元的结果精度就比较差了
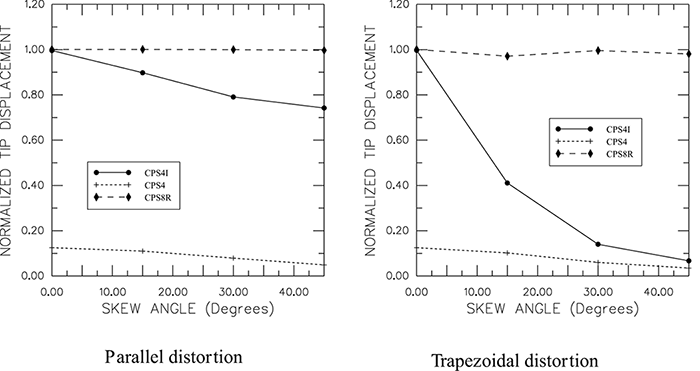
一阶完全积分单元在所有情况下都会产生糟糕结果。二阶缩减积分单元结果非常好,直到单元严重变形才恶化。
当非协调单元为矩形时,即使悬臂梁的厚度上只有1个单元,也可以得到非常好的结果。然而,对单元变形扭曲态敏感。在严重扭曲的网格中,只改变单元类型通常不会产生准确结果。网格变形也要尽量减少。
总结就是,非协调单元可以解决一阶完全积分单元的剪切闭锁问题,且计算成本比二阶缩减积分单元、二阶完全积分单元的成本更低,但缺点在于对网格单元变形十分敏感,要求具有很好的单元质量。
Hybrid elements
混杂单元在几乎所有实例连续单元类型中都是可选的。**混杂单元用于材料不可压缩(泊松比= 0.5)或非常接近不可压缩(泊松比>0.475)的情况。**橡胶是典型的不可压缩材料(出了平面盈应力状态下)
考虑受均匀静水压力作用下的单元:
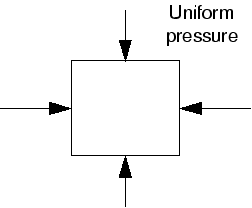
在这样的载荷下,橡胶不会发生体积变化,因此,压力应力( pressure stress)无法根据节点位移得到;基于位移的formulation不适用于任何具有不可压缩材料特性的单元。
混杂单元有一个额外自由度,决定了单元的压力应力。节点位移仅用于计算偏应变(剪切)和应力。
总结就是,混杂单元用于不可压缩材料
个额外自由度,决定了单元的压力应力。节点位移仅用于计算偏应变(剪切)和应力。
总结就是,混杂单元用于不可压缩材料