123.买卖股票的最佳时机III

确定递归函数，当前的每一个状态都由前一天决定。

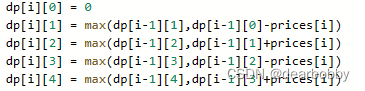
以dp[i][1]和dp[i][2]为例讲解递归函数的含义：

• dp[i][1]=max(dp[i-1][1],dp[i-1][0]-prices[i])
  含义： 第i天的股票第一天持有状态有两种，一种是前一天就持有该股票，另一种是前一天不持有今天购入该股票达到当天持有股票的状态，两者取最大值得到第i天第一次持有股票的最大收益。

• dp[i][2]=max(dp[i-1][2],dp[i-1][1]+prices[i])
  含义： 第i天的股票第一次不持有状态有两种，一种是前一天就不持有该股票，另一种是前一天第一次持有该股票今天将该股票卖出后，获取收益。

在计算的过程中已经自动限制好了两次交易，因而不再需要其他的交易情况。

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        # 最多有两次卖出的机会
        N = len(prices)
        dp = [[0]*5 for i in range(N)]
        dp[0][0] = 0
        dp[0][1] = -prices[0]
        dp[0][2] = 0
        dp[0][3] = -prices[0]
        dp[0][4] = 0
        for i in range(1,N):
            # 因为每一个后续的状态均会保留前面第一天和第二天的状态
            dp[i][0] = 0
            dp[i][1] = max(dp[i-1][1],dp[i-1][0]-prices[i])
            dp[i][2] = max(dp[i-1][2],dp[i-1][1]+prices[i])
            dp[i][3] = max(dp[i-1][3],dp[i-1][2]-prices[i])
            dp[i][4] = max(dp[i-1][4],dp[i-1][3]+prices[i])
        return max(dp[N-1][2],dp[N-1][4])

188.买卖股票的最佳时机IV

区别根据k每次均新建dp矩阵

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        # 最多有两次卖出的机会
        N = len(prices)
        dp = [[0]*(2*k+1) for i in range(N)]
        dp[0][0] = 0
        for i in range(1,2*k+1):
            if i % 2 == 1:
                dp[0][i] = -prices[0]
            else :
                dp[0][i] = 0
        for i in range(1,N):
            # 因为每一个后续的状态均会保留前面第一天和第二天的状态
            for j in range(1,2*k+1):
                if j % 2 == 1:
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-1]-prices[i])
                else:
                    dp[i][j] = max(dp[i-1][j],dp[i-1][j-1]+prices[i])
        return max(dp[N-1])