基于黄金莱维引导机制的阿基米德优化算法(MSAOA)

摘要：针对标准阿基米德优化算法（AOA）在求解优化问题时存在全局探索能力弱、收敛速度慢和求解精度低等问题，提出一种多策略阿基米德优化算法（MSAOA）。首先，利用变区间初始化策略，使得初始种群尽可能地靠近全局最优解，从而提高初始解的质量；其次，提出黄金莱维引导机制，以提高算法在迭代后期的种群多样性；最后，在维持种群多样性的前提下，引入自适应波长算子，以达到提高算法搜索效率的目的。

1.阿基米德优化算法

基础阿基米德优化算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/119999874

2. 改进阿基米德优化算法

2.1 变区间初始化策略

初始化种群的好坏一定程度上决定了算法的性能, 初始 种群在解空间中的细微不同,都可能影响算法进化方向。 $\mathrm{AOA}$ 的初始种群在搜索空间中随机产生, 导致初始种群分 布不均匀, 搜索范围有限。为了解决以上问题, 获得好的初 始种群, 本文利用变区间初始化策略来提取搜索空间中有用 信息以保证种群向全局最优解靠近。
对于优化问题:
$$\min f(t),t_i\in \left[L{B}_i,U{B}_i\right];i\in 1,2,\cdots ,n\text{\hspace{1em}(13)}$$
式中: $LB$ (Lower Bound) 表示搜索空间中的搜索下限; $UB$ (Upper Bound) 表示搜索空间中的搜索上限。变区间初始化策略对就是通过不断缩短 $[\mathbf{LB},U\mathbf{UB}]$, 将初始种群逼近到式 (13) 中近似最优解的附近。
首先在中间取一个中点 $\mathbf{l}$ 。
$$\mathbf{l}=\mathbf{LB}+0.5(\mathbf{UB}-\mathbf{L}B)\text{\hspace{1em}(14)}$$
生成两个个体:
$$\{\begin{array}{l}{x}_1=(a)\\ x_2=(b)\end{array}\text{\hspace{1em}(15)}$$
式中 $\mathbf{a}$ 和 $\mathbf{b}$ 分别为:
$$\{\begin{array}{l}\mathbf{a}=\mathbf{L}\mathbf{B}+\mathrm{rand}(\mathbf{l}-\mathbf{L}\mathbf{B})\\ \mathbf{b}=\mathbf{l}+\mathrm{rand}(\mathbf{U}\mathbf{B}-\mathbf{l})\end{array}\text{\hspace{1em}(16)}$$
计算 $f\left({\mathbf{x}}_1\right)$ 和 $f\left({\mathbf{x}}_2\right)$ 并比较它们大小, 若 $f\left(x_1\right)>f\left({\mathbf{x}}_2\right)$, 则有 ${\mathbf{x}}^{\ast }\in [\mathbf{l},\mathbf{UB}]$, 从而将潜在的最优解位置收缩到 $[\mathbf{l},U\mathbf{B}]$ 内 ; 然 后依次迭代,不断缩短搜索区间, 并将搜索空间 $[\mathbf{LB},U\mathbf{B}]$ 分 割成 $n-1$ 个子区间, 把初始种群聚集到问题(13)的最优解 附近。

2.2 黄金莱维引导机制

其次, 本文引人正弦函数与单位圆之间的关系 ${}^{[19]}$, 使得 种群能遍历正弦函数上的所有点, 即单位圆上的所有点。个 体位置更新公式为:
$$\begin{array}{rl}& \\ & {\mathbf{X}}_{\text{new }}^{t+1}=X^t\times \left|\sin \left(R_1\right)\right|+R_2\times \sin \left(R_1\right)\times s\oplus \text{ dis }\end{array}\text{\hspace{1em}(19)}$$

$$\begin{array}{rl}& \text{ dis }=\left|{\theta }_1\times X_{\text{best }}^t-{\theta }_2\times X_i^t\right|\end{array}\text{\hspace{1em}(20)}$$

式中: $R_1\in [0,2\pi ]$ 的随机数, $R_1$ 和莱维步长 $s$ 共同决定搜索半 径; $R_2\in [0,\pi ]$ 的随机数,决定个体的位置更新方向; ${\theta }_1$ 和 ${\theta }_2$ 是 引人的黄金分割系数 $\tau$, 其目的是缩小搜索空间, 使得算法 在每次迭代都会对能产生优秀解的区域进行充分搜索,从而 加快了算法收敛速度。公式中具体参数表达式如下所示:
$$\{\begin{array}{l}{\theta }_1=-\pi +2\pi \times (1-\tau )\\ {\theta }_2=-\pi +2\pi \times \tau \\ \tau =(\sqrt{5}-2)/2\end{array}\text{\hspace{1em}(21)}$$
最后, 虽然对目标个体使用黄金莱维引导机制, 能让算 法跳出局部最优,但并不能保证新的个体位置优于原目标个 体位置, 因此在引导机制后加人贪婪机制, 通过比较个体位 置更新前后个体适应度后再决定是否更新目标位置, 以保留 适应度较好的个体。贪婪机制具体操作表达式如下：
$$X_i^{t+1}=\{\begin{array}{ll}{X}_i^{t+1},& \text{ fit }\left(X_i^{t+1}\right)>fit\left(X_{\text{new }}^{t+1}\right)\\ X_{\text{new }}^{t+1},& \text{ fit }\left(X_i^{t+1}\right)⩽\text{ fit }\left(X_{\text{new }}^{t+1}\right)\end{array}\text{\hspace{1em}(22)}$$

2.3 自适应波长算子

受到浸泡在液体中运动物体会导致水平面发生波动现 象启发, 本文提出了自适应波长算子: 达到自身平衡(适应度 较好) 的个体, 引起波动较小, 从而具有较长的波长; 还远末 达到自身平衡(适应度较差) 的个体运动会引起的较大波动, 从而具有较短的波长。
在 $\mathrm{AOA}$ 中, 由于缺乏多样性的操作, 当 $\mathrm{AOA}$ 进化到一定 的程度时, 导致 AOA 很难从自身适应度获取收益。因此结 合浸泡在液体中运动物体的物理现象, 本文提出自适应波长 算子增强个体学习效率, 提高算法寻优精度。
$${\lambda }_i={\alpha }^{-\left(f\left(X_i\right)-f_{\min }+\epsilon \right)/\left(f_{\max }-f_{\min }+\epsilon \right)}\text{\hspace{1em}(23)}$$
式中: ${\lambda }_i$ 表示第 $i$ 个体运动引起的波长系数; $f\left(X_i\right)$ 表示当前 迭代中第 $i$ 个个体的适应度值; $f_{\min }$ 和 $f_{\text{max }}$ 分别表示当前迭代 中最优适应度值和最差适应度值; $\alpha$ 为衰减因子, $\epsilon$ 为一个非 常小的有理数, 以防止分母为 0 的情况。最后将自适应波长 系数融合到密度因子, 得到新密度因子更新公式为:
$$d_i^{l+1}=1.5\times \exp \left(\left(t_{\text{max }}-t\right)/t_{\text{max }}\right)-{\lambda }_i\left(t/t_{\max }\right)\text{\hspace{1em}(24)}$$
式中 $d_i^{t+1}$ 表示在 $t+1$ 代中第 $i$ 个个体的密度因子。新的密度 因子的大小会根据个体自身适应度动态变化: 适应度接近最 优适应度的个体, $\mathrm{AOA}$ 保持原来的密度因子的性质; 而适应 度较差的个体, 密度因子接近最大值, 使当前个体拥有较长 的步长, 快速向最优解靠近。

3.实验结果

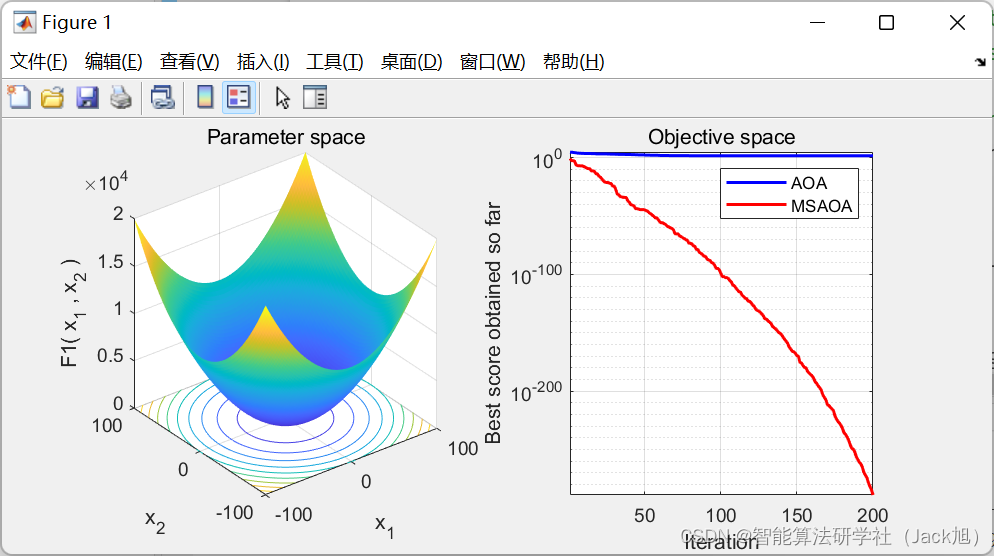
4.参考文献

[1]陈俊,何庆,李守玉.基于黄金莱维引导机制的阿基米德优化算法[J].计算机应用,2022,42(09):2807-2815.

5.Matlab代码

6.Python代码