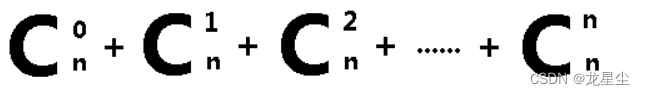CSP-S 第一轮笔试重点题

news2024/11/7 13:47:30

CSP-S提高组笔试题重点题汇总：

今天我给大家分享一些 CSP-S 第一轮笔试中的一些重点题，包含讲解。

第一题：

1.十进制小数13.375对应的二进制数是（）。

A.1101.011

B.1011.011

C.1101.101

D.1010.01

解析：

  大家肯定都对一个十进制整数转为二进制有些了解（假设这个十进制整数为x，先求出x除以2的余数，为几久代表这个二进制为上的数是几，然后不断的除以二向下取整，知道x为0为止。十进制整数转k进制道理也是一样，就是变成不断求出x除以k的余数了）。



但是对于小数的二进制，我们可以进一步深究，首先求出整数的二进制，13转为二进制就是1101，接下来剩下0.375，现在我们要先算出2的负n次方，这个就相当于是2求的n次方的倒数（如2^-1=1/2 2^-2=1/4 2^3=1/8）。



接下来就来看小数怎么转成2的负数进制了，不同于整数，它是不断的乘以2，如果乘了2之后整数部分还是为0，那么当前2的负数进制就为0，如果整数部分为1那么当前2的负数进制就为1，然后去掉整数部分，留下小数部分继续算，知道去掉整数部分后值为0为止。



我们先来举一个例子，比如说0.75，它的二进制应该为0.11（因为0.75=2^-1+2^-2），按照上述方法进行推导：

1.0.75*2=1.5 -------------------- 当前位为1

2.1.5-1=0.5 -------------------- 去掉整数部分

3.0.5*2=1 -------------------- 当前位为1

4.1-1=0 -------------------- 结束

这样就可以得到二进制序列0.11。



然后我们来求题目要求的0.375的二进制序列:

0.375*2=0.75 ------- 当前位为0
0.75*2=1.5   ------- 当前位为1
1.5-1=0.5 ------- 去掉整数部分
0.5*2=1 ------- 当前位为1
1-1=0   ------- 结束

这样就得到了0.011这个二进制序列，算上之前整数部分的二进制序列，那么答案就是1101.011.所以我们选择A。

答案：

第二题：

2.为解决web应用中的不兼容问题,保障信息的顺利流通,( )制定了一系列标准,涉及HTML、XML、CSS等,并建议开发者遵循。

A. 微软

B. 美国计算机协会(ACM)

C. 联合国教科文组织

D. 万维网联盟(W3C)

解析：

万维网联盟（外语缩写：W3C）标准不是某一个标准，而是一系列标准的集合。网页主要由三部分组成：结构（Structure）、表现（Presentation）和行为（Behavior）。

万维网联盟创建于1994年，是Web技术领域最具权威和影响力的国际中立性技术标准机构。到目前为止，W3C已发布了200多项影响深远的Web技术标准及实施指南，如广为业界采用的超文本标记语言（标准通用标记语言下的一个应用）、可扩展标记语言（标准通用标记语言下的一个子集）以及帮助残障人士有效获得Web内容的信息无障碍指南（WCAG）等，有效促进了Web技术的互相兼容，对互联网技术的发展和应用起到了基础性和根本性的支撑作用。

对应的标准也分三方面：结构化标准语言主要包括XHTML和XML，表现标准语言主要包括CSS，行为标准主要包括对象模型（如W3C DOM）、ECMAScript等。这些标准大部分由W3C起草和发布，也有一些是其他标准组织制订的标准，比如ECMA（European Computer Manufacturers Association）的ECMAScript标准。

通过以上的资料查找，我们选择D。（这种是最难的，和历史差不多，全靠记）

答案：

第三题：

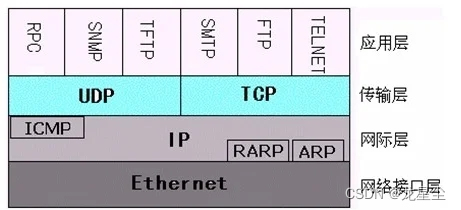
3.在TCP/IP协议簇中,最核心的网络协议是（）

A.UDP

B.HTTP

C.TCP

D.IP

解析：

TCP/IP是有共网络接口层，网络层，运输层和应用层共四层协议系统。

第一层是应用层，功能是服务于应用进程的，就是向用户提供数据加上编码和对话对的控制。

第二层是运输层，功能是能够解决诸如端到端可靠性和保证数据按照正确的顺序到达。包括所给数据应该送给哪个应用程序。

第三层是网络层，功能是进行网络连接的建立，和终止及IP地址的寻找最佳途径等功能。

第四层是网络接口层，功能是传输数据的物理媒介，是数据包从一个设备的网络层传输到另外一个设备的网络层的方法。还有控制组成网络的硬件设备。

通过查找资料，可以看到在协议系统中IP所占区域最大，所以我们选择D。

答案：

第四题：

4.定义L数:素数或者是回文数满足两者中任意一个条件的数。大于等于10并且小于等于120的“L数”共有多少个? (注:回文数指从左到右读与从右到左读是相同的，如“121”、“1331”;两个条件都成立也是L数，如“131”) （）

A.34

B.35

C.36

D.37

解析：

我们可以先找到所有的素数和所有的回文数，然后减去重复的部分。



  10~120以内的质数：

  11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113

总共有着26个.



10~120以内的回文数：

  11,22,33,44,55,66,77,88,99,101,111.

  总共有着11个.



两者之间重复的数字有11和101，那么求出答案26+11-2=35，所以我们选择B。

答案：

B

第五题：

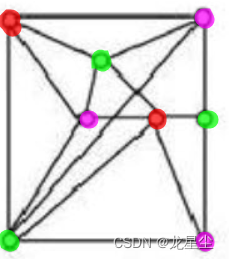
5.对图G中各个结点分别指定一种颜色，使相邻结点颜色不同，则称为图G的一个正常着色。正常着色图G所必需的最少颜色数，称为G的色数。那么下图的色数是（）

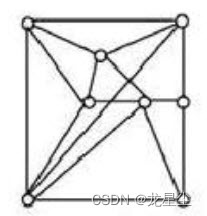
A. 3

B. 4

C. 5

D. 6

解析：

大家应该都听说过四色原理吧，这里简要说明一下：“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”用数学语言表示，即“将平面任意地细分为不相重叠的区域，每一个区域总可以用1，2，3，4这四个数字之一来标记，而不会使相邻的两个区域得到相同的数字。”

但是大家不要看到这种类型题都选择4，因为有些图我们只用三种颜色也可以进行表示，将上图进行涂色之后为：

可以用三种颜色进行涂色，所以我们选择A。

答案：

A

第六题：

6.设含有10个元素的集合的全部子集数为S，其中由7个元素组成的子集数为T，则T/S的值为（B）。

A.5/32

B.15/128

C.1/8

D.21/128

解析：

首先给大家讲一下子集是什么：

子集是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。

符号语言：若∀a∈A，均有a∈B，则A⊆B。

  我们该如何求子集的个数呢？

假设一个集合包含n个元素，要求计算该集合的子集个数。

该集合的所有子集，也叫该集合的幂集，比如集合{1,2,3}的所有子集为空集，{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}数一数，一共8个，由此推测为2的三次方，即2的三次幂。那么这个结论是否正确呢？



我们知道具有n个元素的集合的子集其实就是空集，含有一个元素的集合，含有两个元素的集合...含有n个元素集合，这集合的和就是：

根据多项式的公式和定理知道，上面式子之和为2的n次方。



然后我们回来看题目，一个集合有10个元素，那么这个集合的子集就是2^10=1024，然后再这10个数字中选7个出来，就是 $_{C_{10}^{7}\textrm{}}^{}\textrm{}$ ，C(n,m) 表示在n个数中选m个数的组合个数，相当于 $\frac{n!}{(n-m)!m!}$ ，那么 $_{}^{}\textrm{C}_{10}^{7}\textrm{}\doteq \frac{10!}{(10-7)!7!}=\frac{10!}{3!7!}=\frac{10*9*8}{2*3}=5*3*8=120$ ，然后我们可以将 $\frac{120}{1024}$ 进行约分，就等于 $\frac{15}{128}$ 。



所以我们选择B。