基于BP神经网络对MNIST数据集检测识别
- 1.作者介绍
- 2.基于BP神经网络对MNIST数据集检测识别
- 2.1 BP神经网络介绍
- 2.2 神经元模型
- 2.3 激活函数
- 2.4 BP神经网络基础架构
- 2.5 BP神经网络正向传播反向传播
- 3.基于BP神经网络对MNIST数据集检测识别实验
- 3.1 MNIST数据集介绍
- 3.2代码实现(Pytorch版本)
- 3.3代码实现(TensorFlow版本)
- 4. BP神经网络注意问题
- 4.1 代码相关问题
1.作者介绍
任陇刚,男,西安工程大学电子信息学院,2022级研究生
研究方向:机器视觉与人工智能
电子邮件:1756769702@qq.com
张思怡,女,西安工程大学电子信息学院,2022级研究生,张宏伟人工智能课题组
研究方向:机器视觉与人工智能
电子邮件:981664791@qq.com
2.基于BP神经网络对MNIST数据集检测识别
2.1 BP神经网络介绍
首先从名称中可以看出,Bp神经网络可以分为两个部分,bp和神经网络。bp是 Back Propagation 的简写 ,意思是反向传播。BP网络能学习和存贮大量的输入-输出模式映射关系,而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的误差平方和最小。其主要的特点是:信号是正向传播的,而误差是反向传播的。算法流程图如下:
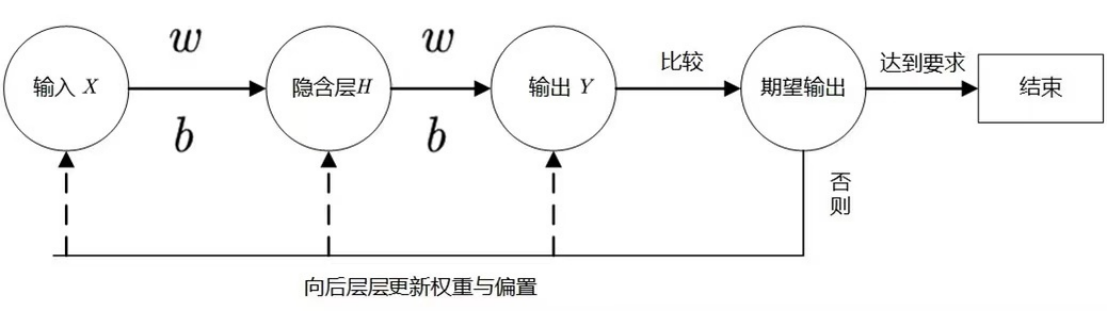
2.2 神经元模型
每个神经元都接受来自其它神经元的输入信号,每个信号都通过一个带有权重的连接传递,神经元把这些信号加起来得到一个总输入值,然后将总输入值与神经元的阈值进行对比(模拟阈值电位),然后通过一个“激活函数”处理得到最终的输出(模拟细胞的激活),这个输出又会作为之后神经元的输入一层一层传递下去。神经元模型如下:
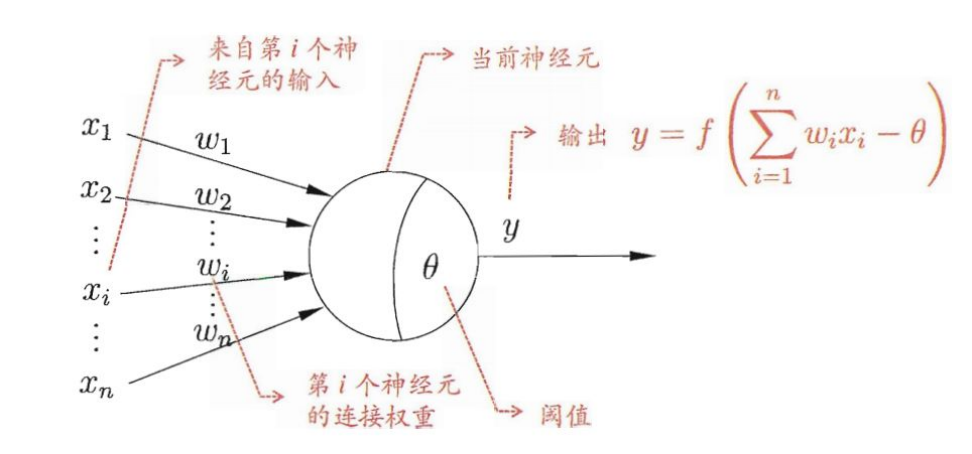
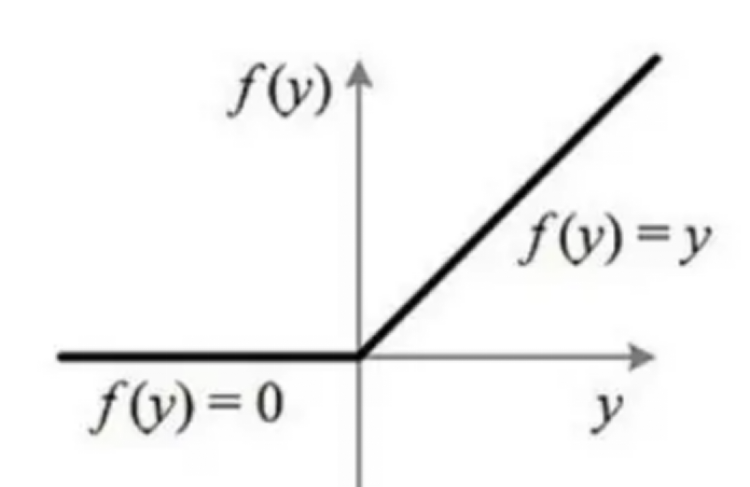
2.3 激活函数
引入激活函数的目的是在模型中引入非线性。如果没有激活函数(其实相当于激励函数是f(x) = x),那么无论你的神经网络有多少层,最终都是一个线性映射,那么网络的逼近能力就相当有限,单纯的线性映射无法解决线性不可分问题。正因为上面的原因,我们决定引入非线性函数作为激励函数,这样深层神经网络表达能力就更加强大
BP神经网络算法常用的激活函数:
1)Sigmoid(logistic),也称为S型生长曲线,函数在用于分类器时,效果更好。
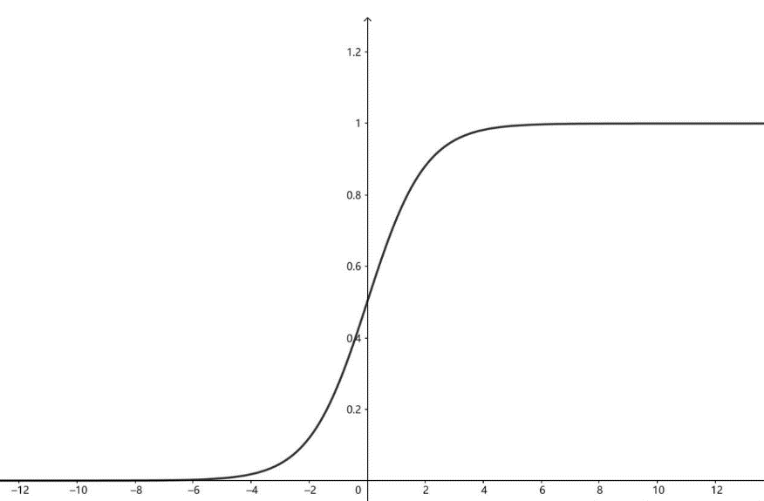
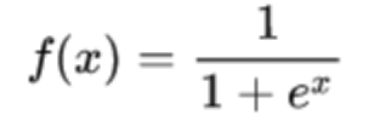
2)Tanh函数(双曲正切函数),解决了logistic中心不为0的缺点,但依旧有梯度易消失的缺点。
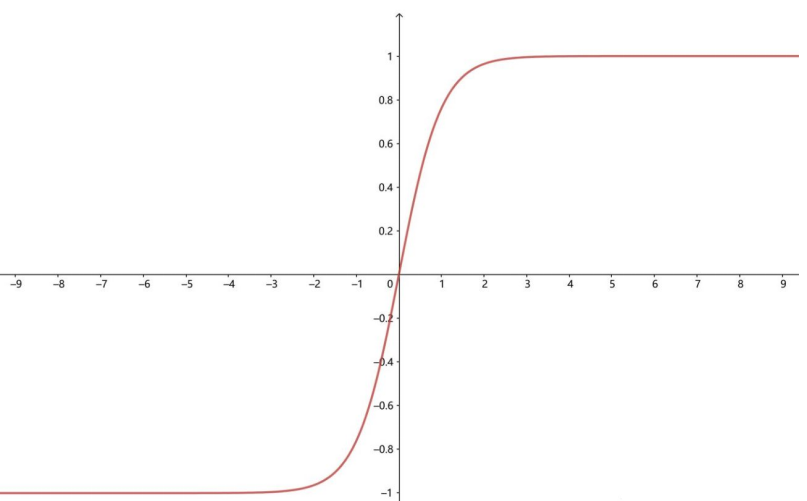
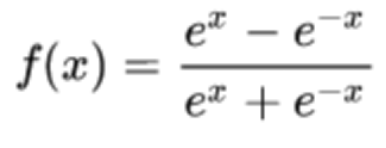
3)relu函数是一个通用的激活函数,针对Sigmoid函数和tanh的缺点进行改进的,目前在大多数情况下使用
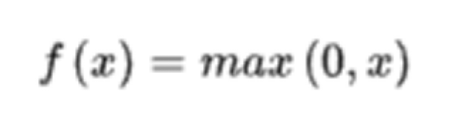
2.4 BP神经网络基础架构
BP网络由输入层、隐藏层、输出层组成
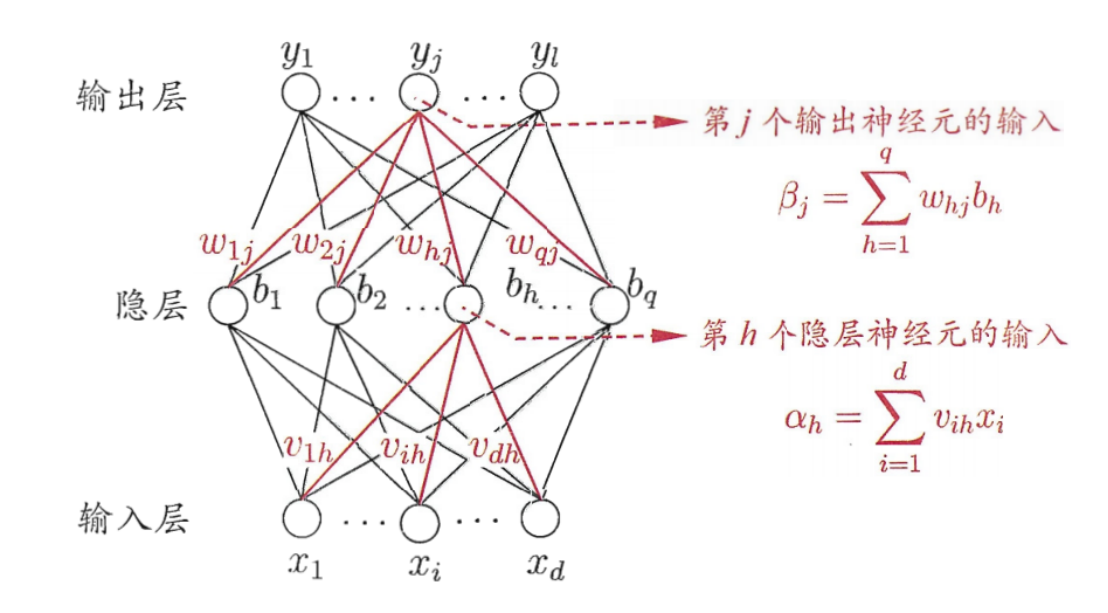
输入层:信息的输入端,是读入你输入的数据的
隐藏层:信息的处理端,可以设置这个隐藏层的层数(在这里一层隐藏层,q个神经元)
输出层:信息的输出端,也就是我们要的结果
对于上图的只含一个隐藏层的神经网络模型:BP神经网络的过程主要分为两个阶段,
第一阶段是信号的正向传播,从输入层经过隐含层,最后到达输出层;
第二阶段是误差的反向传播,从输出层到隐含层,最后到输入层,依次调节隐含层到输出层的权重和偏置,输入层到隐含层的权重和偏置
2.5 BP神经网络正向传播反向传播
正向传播过程
正向传播就是让信息从输入层进入网络,依次经过每一层的计算,得到最终输出层结果的过程
从输入层到隐藏层:
从隐藏层到输出层:
以y1举例。y1里的输出自然有来自b1,b2,…bq的。那么分别按照权重去乘。
类似的我们可以求解出y2……yn
反向传播过程
基本思想就是通过计算输出层与期望值之间的误差来调整网络参数,从而使得误差变小。
计算误差公式如下:(差值的平方)
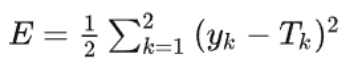
如何调整权重的大小,才能使损失函数不断地变小呢?
1.梯度下降法
2.(随机梯度下降)SGD
3.(自适应优化)Adam
3.基于BP神经网络对MNIST数据集检测识别实验
3.1 MNIST数据集介绍
MNIST 数据集可在 http://yann.lecun.com/exdb/mnist/ 获取,它包含了四个部分:
•Training set images: train-images-idx3-ubyte.gz (9.9 MB, 解压后 47 MB, 包含 60,000 个样本)
•Training set labels: train-labels-idx1-ubyte.gz (29 KB, 解压后 60 KB, 包含 60,000 个标签)
•Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 解压后 7.8 MB, 包含 10,000 个样本)
•Test set labels: t10k-labels-idx1-ubyte.gz (5KB, 解压后 10 KB, 包含 10,000 个标签)
Mnist数据集中的标签是介于0~9的数字,Mnist中的标签是用独热编码(one-hot-vectors)表示的,一个one-hot向量除了某一位数字是1以外,其余维度的数组都是0,比如标签0用独热编码表示为([1, 0, 0, 0, 0, 0, 0, 0, 0, 0]),标签3用独热编码表示为([0, 0, 0, 1, 0, 0, 0, 0, 0, 0])。所以,Mnist数据集中所有的标签mnist.train.labels是一个[60000, 10]的数字矩阵。
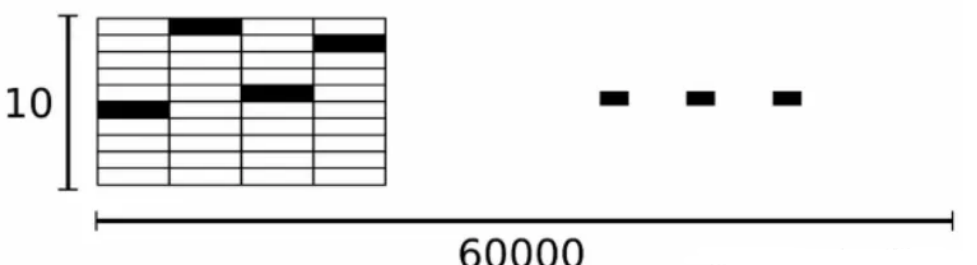
训练图片和测试图片:
每一张图片包含2828个像素。Mnist数据集把代表一张图片的二维数据转开成一个向量,长度为2828=784。因此在Mnist的训练数据集中mnist.train.images是一个形状为[60000, 784]的张量,第一个维度数字用来索引图片,第二个维度数字用来索引每张图片中的像素点,图片里的某个像素的强度值介于0-1之间。(图8部分数据可视化)


3.2代码实现(Pytorch版本)
定义transform对象,其定义了数据集中的图片应该做怎样的处理:
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)), ])
加载和下载训练测试数据集,这里使用pytorch提供的API进行下载:
train_set = datasets.MNIST('data', # 下载到该文件夹下
download=not os.path.exists('train_set'), # 是否下载,如果下载过,则不重复下载
train=True, # 是否为训练集
transform=transform # 要对图片做的transform
)
print(train_set)
test_set = datasets.MNIST('data',
download=not os.path.exists('test_set'),
train=False,
transform=transform
)
print(test_set)
构建训练数据集和测试数据集的DataLoader对象:
train_loader = torch.utils.data.DataLoader(train_set, batch_size=128, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=128, shuffle=True)
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
在上面,batch_size=64,每个batch送进64张图片每个图片只有一个通道(灰度图),大小为28x28。抽一张绘制一下:
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r');
定义神经网络:
class NerualNetwork(nn.Module):
def __init__(self):
super().__init__()
"""
定义第一个线性层,
输入为图片(28x28),
输出为第一个隐层的输入,大小为128。
"""
self.linear1 = nn.Linear(28 * 28, 128)
# 在第一个隐层使用ReLU激活函数
self.relu1 = nn.ReLU()
"""
定义第二个线性层,
输入是第一个隐层的输出,
输出为第二个隐层的输入,大小为64。
"""
self.linear2 = nn.Linear(128, 64)
# 在第二个隐层使用ReLU激活函数
self.relu2 = nn.ReLU()
"""
定义第三个线性层,
输入是第二个隐层的输出,
输出为输出层,大小为10
"""
self.linear3 = nn.Linear(64, 10)
# 最终的输出经过softmax进行归一化
self.softmax = nn.LogSoftmax(dim=1)
# 上述操作可以直接使用nn.Sequential写成如下形式:
self.model = nn.Sequential(nn.Linear(28 * 28, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1)
)
网络前向传播
def forward(self, x):
"""
定义神经网络的前向传播
x: 图片数据, shape为(64, 1, 28, 28)
"""
# 首先将x的shape转为(64, 784)
x = x.view(x.shape[0], -1)
# 接下来进行前向传播
x = self.linear1(x)
x = self.relu1(x)
x = self.linear2(x)
x = self.relu2(x)
x = self.linear3(x)
x = self.softmax(x)
# 上述一串,可以直接使用 x = self.model(x) 代替。
return x
模型实例化:
定义损失函数,这里选用负对数似然损失函数(NLLLoss, negative log likelihood loss),其常用于分类任务
定义优化器,这里使用随机梯度下降法,学习率设置为0.003,momentum取默认的0.9(用于防止过拟合)
model = NerualNetwork()
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003, momentum=0.9)
模型训练过程:
time0 = time() # 记录下当前时间
epochs = 15 # 一共训练15轮
for e in range(epochs):
running_loss = 0 # 本轮的损失值
for images, labels in train_loader:
# 前向传播获取预测值
output = model(images)
# 计算损失
loss = criterion(output, labels)
# 进行反向传播
loss.backward()
# 更新权重
optimizer.step()
# 清空梯度
optimizer.zero_grad()
# 累加损失
running_loss += loss.item()
else:
# 一轮循环结束后打印本轮的损失函数
print("Epoch {} - Training loss: {}".format(e+1, running_loss / len(train_loader)))
# 打印总的训练时间
print("\nTraining Time (in minutes) =", (time() - time0) / 60)
correct_count, all_count = 0, 0
model.eval() # 将模型设置为评估模式
# 从test_loader中一批一批加载图片
for images, labels in test_loader:
# 循环检测这一批图片
for i in range(len(labels)):
logps = model(images[i]) # 进行前向传播,获取预测值
probab = list(logps.detach().numpy()[0]) # 将预测结果转为概率列表。[0]是取第一张照片的10个数字的概率列表(因为一次只预测一张照片)
pred_label = probab.index(max(probab)) # 取最大的index作为预测结果
true_label = labels.numpy()[i]
if (true_label == pred_label): # 判断是否预测正确
correct_count += 1
all_count += 1
print("Number Of Images Tested =", all_count)
print("\nModel Accuracy ={}%".format((correct_count / all_count)*100))
完整代码:
import os
import numpy as np
import torch
import torchvision
import matplotlib.pyplot as plt
from time import time
from torchvision import datasets, transforms
from torch import nn, optim
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,)), ])
train_set = datasets.MNIST('data', # 下载到该文件夹下
download=not os.path.exists('train_set'), # 是否下载,如果下载过,则不重复下载
train=True, # 是否为训练集
transform=transform # 要对图片做的transform
)
print(train_set)
test_set = datasets.MNIST('data',
download=not os.path.exists('test_set'),
train=False,
transform=transform
)
print(test_set)
train_loader = torch.utils.data.DataLoader(train_set, batch_size=128, shuffle=True)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=128, shuffle=True)
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r');
class NerualNetwork(nn.Module):
def __init__(self):
super().__init__()
"""
定义第一个线性层,
输入为图片(28x28),
输出为第一个隐层的输入,大小为128。
"""
self.linear1 = nn.Linear(28 * 28, 128)
# 在第一个隐层使用ReLU激活函数
self.relu1 = nn.ReLU()
"""
定义第二个线性层,
输入是第一个隐层的输出,
输出为第二个隐层的输入,大小为64。
"""
self.linear2 = nn.Linear(128, 64)
# 在第二个隐层使用ReLU激活函数
self.relu2 = nn.ReLU()
"""
定义第三个线性层,
输入是第二个隐层的输出,
输出为输出层,大小为10
"""
self.linear3 = nn.Linear(64, 10)
# 最终的输出经过softmax进行归一化
self.softmax = nn.LogSoftmax(dim=1)
# 上述操作可以直接使用nn.Sequential写成如下形式:
self.model = nn.Sequential(nn.Linear(28 * 28, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.LogSoftmax(dim=1)
)
def forward(self, x):
"""
定义神经网络的前向传播
x: 图片数据, shape为(64, 1, 28, 28)
"""
# 首先将x的shape转为(64, 784)
x = x.view(x.shape[0], -1)
# 接下来进行前向传播
x = self.linear1(x)
x = self.relu1(x)
x = self.linear2(x)
x = self.relu2(x)
x = self.linear3(x)
x = self.softmax(x)
# 上述一串,可以直接使用 x = self.model(x) 代替。
return x
model = NerualNetwork()
criterion = nn.NLLLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003, momentum=0.9)
time0 = time() # 记录下当前时间
epochs = 15 # 一共训练15轮
for e in range(epochs):
running_loss = 0 # 本轮的损失值
for images, labels in train_loader:
# 前向传播获取预测值
output = model(images)
# 计算损失
loss = criterion(output, labels)
# 进行反向传播
loss.backward()
# 更新权重
optimizer.step()
# 清空梯度
optimizer.zero_grad()
# 累加损失
running_loss += loss.item()
else:
# 一轮循环结束后打印本轮的损失函数
print("Epoch {} - Training loss: {}".format(e+1, running_loss / len(train_loader)))
# 打印总的训练时间
print("\nTraining Time (in minutes) =", (time() - time0) / 60)
correct_count, all_count = 0, 0
model.eval() # 将模型设置为评估模式
# 从test_loader中一批一批加载图片
for images, labels in test_loader:
# 循环检测这一批图片
for i in range(len(labels)):
logps = model(images[i]) # 进行前向传播,获取预测值
probab = list(logps.detach().numpy()[0]) # 将预测结果转为概率列表。[0]是取第一张照片的10个数字的概率列表(因为一次只预测一张照片)
pred_label = probab.index(max(probab)) # 取最大的index作为预测结果
true_label = labels.numpy()[i]
if (true_label == pred_label): # 判断是否预测正确
correct_count += 1
all_count += 1
print("Number Of Images Tested =", all_count)
print("\nModel Accuracy ={}%".format((correct_count / all_count)*100))
3.3代码实现(TensorFlow版本)
加载数据
#加载数据
mnist = tf.keras.datasets.mnist
(train_x,train_y),(test_x,test_y) = mnist.load_data()
print('\n train_x:%s, train_y:%s, test_x:%s, test_y:%s'%(train_x.shape,train_y.shape,test_x.shape,test_y.shape))
数据预处理
#归一化、并转换为tensor张量,数据类型为float32.
X_train,X_test = tf.cast(train_x/255.0,tf.float32),tf.cast(test_x/255.0,tf.float32)
y_train,y_test = tf.cast(train_y,tf.int16),tf.cast(test_y,tf.int16)
建立模型(单层隐含层的神经网络)
#建立模型
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=(28,28))) #添加Flatten层说明输入数据的形状
model.add(tf.keras.layers.Dense(128,activation='relu')) #添加隐含层,为全连接层,128个节点,relu激活函数
model.add(tf.keras.layers.Dense(10,activation='softmax')) #添加输出层,为全连接层,10个节点,softmax激活函数
print('\n',model.summary()) #查看网络结构和参数信息
配置模型训练方法
#配置模型训练方法
#adam算法参数采用keras默认的公开参数,损失函数采用稀疏交叉熵损失函数,准确率采用稀疏分类准确率函数
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',metrics=['sparse_categorical_accuracy'])
评估模型
#评估模型
model.evaluate(X_test,y_test,verbose=2) #每次迭代输出一条记录,来评价该模型是否有比较好的泛化能力
保存模型
#保存整个模型
model.save('mnist_weights.h5')
结果可视化
#结果可视化
print(history.history)
loss = history.history['loss'] #训练集损失
val_loss = history.history['val_loss'] #测试集损失
acc = history.history['sparse_categorical_accuracy'] #训练集准确率
val_acc = history.history['val_sparse_categorical_accuracy'] #测试集准确率
运行结果
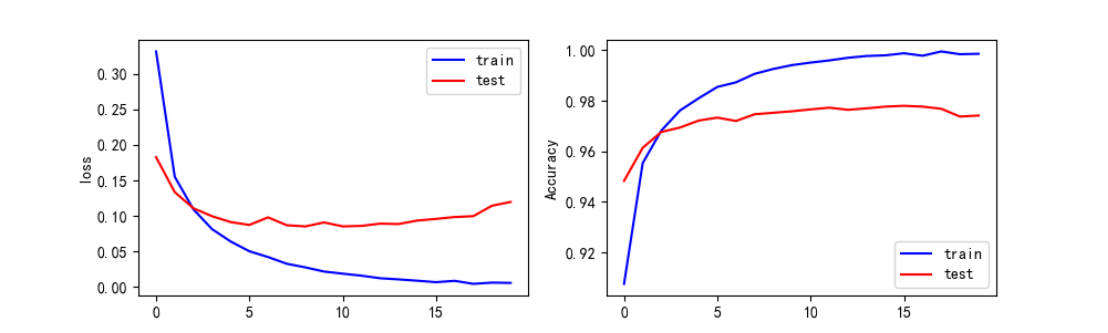
测试结果


完整代码:
########手写数字数据集##########
###########保存模型############
########1层隐含层(全连接层)##########
#60000条训练数据和10000条测试数据,28x28像素的灰度图像
#隐含层激活函数:ReLU函数
#输出层激活函数:softmax函数(实现多分类)
#损失函数:稀疏交叉熵损失函数
#输入层有784个节点,隐含层有128个神经元,输出层有10个节点
import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np
import time
print('--------------')
nowtime = time.strftime('%Y-%m-%d %H:%M:%S')
print(nowtime)
#指定GPU
import os
os.environ["CUDA_VISIBLE_DEVICES"] = "0"
# gpus = tf.config.experimental.list_physical_devices('GPU')
# tf.config.experimental.set_memory_growth(gpus[0],True)
#初始化
plt.rcParams['font.sans-serif'] = ['SimHei']
#加载数据
mnist = tf.keras.datasets.mnist
(train_x,train_y),(test_x,test_y) = mnist.load_data()
print('\n train_x:%s, train_y:%s, test_x:%s, test_y:%s'%(train_x.shape,train_y.shape,test_x.shape,test_y.shape))
#数据预处理
#X_train = train_x.reshape((60000,28*28))
#Y_train = train_y.reshape((60000,28*28)) #后面采用tf.keras.layers.Flatten()改变数组形状
#归一化、并转换为tensor张量,数据类型为float32.
X_train,X_test = tf.cast(train_x/255.0,tf.float32),tf.cast(test_x/255.0,tf.float32)
y_train,y_test = tf.cast(train_y,tf.int16),tf.cast(test_y,tf.int16)
#建立模型
model = tf.keras.Sequential()
model.add(tf.keras.layers.Flatten(input_shape=(28,28))) #添加Flatten层说明输入数据的形状
model.add(tf.keras.layers.Dense(128,activation='relu')) #添加隐含层,为全连接层,128个节点,relu激活函数
model.add(tf.keras.layers.Dense(10,activation='softmax')) #添加输出层,为全连接层,10个节点,softmax激活函数
print('\n',model.summary()) #查看网络结构和参数信息
#配置模型训练方法
#adam算法参数采用keras默认的公开参数,损失函数采用稀疏交叉熵损失函数,准确率采用稀疏分类准确率函数
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',metrics=['sparse_categorical_accuracy'])
#训练模型
#批量训练大小为64,迭代5次,测试集比例0.2(48000条训练集数据,12000条测试集数据)
print('--------------')
nowtime = time.strftime('%Y-%m-%d %H:%M:%S')
print('训练前时刻:'+str(nowtime))
history = model.fit(X_train,y_train,batch_size=64,epochs=30,validation_split=0.2)
print('--------------')
nowtime = time.strftime('%Y-%m-%d %H:%M:%S')
print('训练后时刻:'+str(nowtime))
#评估模型
model.evaluate(X_test,y_test,verbose=2) #每次迭代输出一条记录,来评价该模型是否有比较好的泛化能力
#保存模型参数
#model.save_weights('C:\\Users\\xuyansong\\Desktop\\深度学习\\python\\MNIST\\模型参数\\mnist_weights.h5')
#保存整个模型
model.save('mnist_weights.h5')
#结果可视化
print(history.history)
loss = history.history['loss'] #训练集损失
val_loss = history.history['val_loss'] #测试集损失
acc = history.history['sparse_categorical_accuracy'] #训练集准确率
val_acc = history.history['val_sparse_categorical_accuracy'] #测试集准确率
plt.figure(figsize=(10,3))
plt.subplot(121)
plt.plot(loss,color='b',label='train')
plt.plot(val_loss,color='r',label='test')
plt.ylabel('loss')
plt.legend()
plt.subplot(122)
plt.plot(acc,color='b',label='train')
plt.plot(val_acc,color='r',label='test')
plt.ylabel('Accuracy')
plt.legend()
#暂停5秒关闭画布,否则画布一直打开的同时,会持续占用GPU内存
#根据需要自行选择
#plt.ion() #打开交互式操作模式
#plt.show()
#plt.pause(5)
#plt.close()
#使用模型
plt.figure()
for i in range(10):
num = np.random.randint(1,10000)
plt.subplot(2,5,i+1)
plt.axis('off')
plt.imshow(test_x[num],cmap='gray')
demo = tf.reshape(X_test[num],(1,28,28))
y_pred = np.argmax(model.predict(demo))
plt.title('标签值:'+str(test_y[num])+'\n预测值:'+str(y_pred))
y_pred = np.argmax(model.predict(X_test[0:5]),axis=1)
print('X_test[0:5]: %s'%(X_test[0:5].shape))
print('y_pred: %s'%(y_pred))
plt.ion() #打开交互式操作模式
plt.show()
plt.pause(5)
plt.close()
4. BP神经网络注意问题
a)参数选取很重要。 用最基本的BP 算法来训练BP 神经网络时,学习率、均方误差、权值、阈值的设置都对网络的训练均有影响。综合选取合理的值,将有利于网络的训练。在最基本的BP 算法中,学习率在整个训练过程是保持不变的,学习率过大,算法可能振荡而不稳定;学习率过小,则收敛速度慢,训练时间长。
b)存在麻痹现象。由于优化的目标函数很复杂,它必然会在神经元输出接近0或1的情况下,出现一些平坦区,在这些区域内,权值误差改变很小,使训练过程几乎停顿;
c) 搜索步长提前确定。 为了使网络执行BP算法,不能用传统的一维搜索法求每次迭代的步长,而必须把步长的更新规则预先赋予网络,这种方法将引起算法低效。
不同epoch下的Accurary可视化结果:
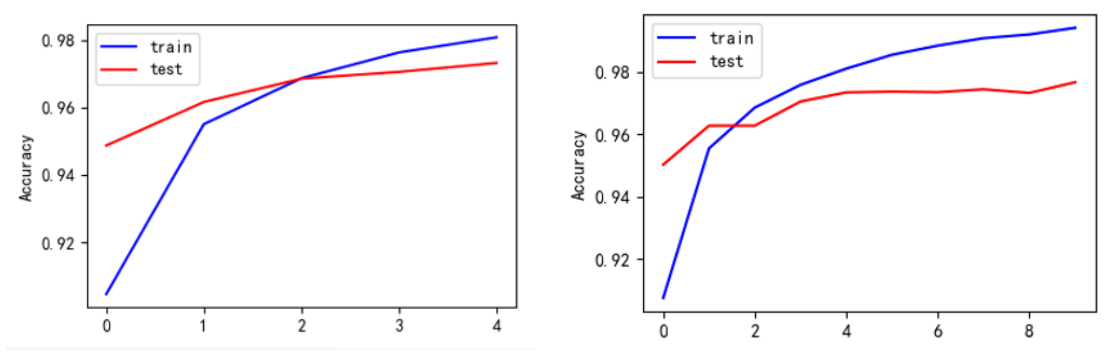
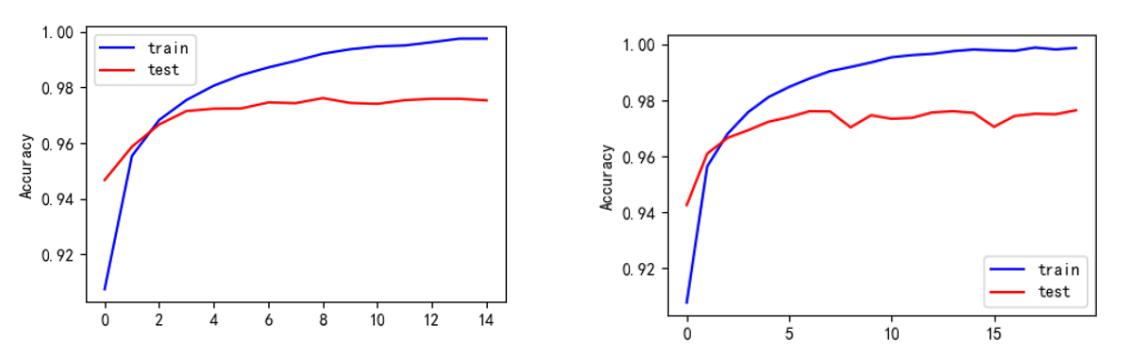
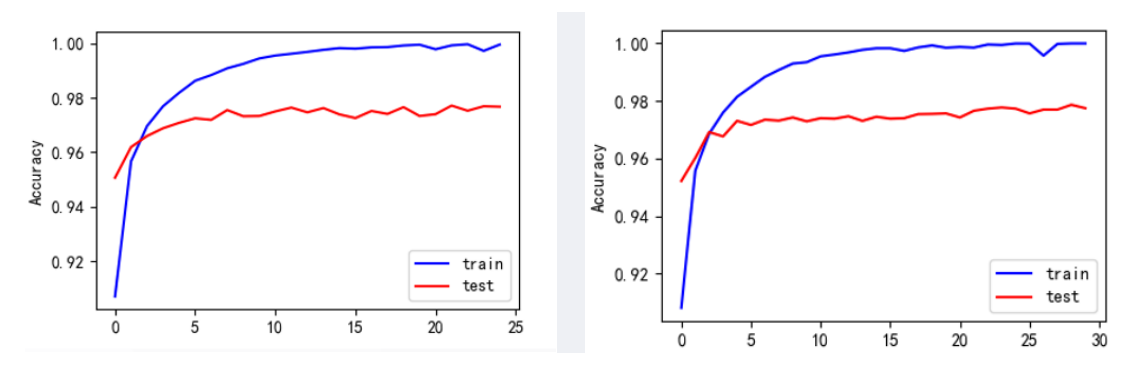
4.1 代码相关问题
Dataloader中num_worker设置


•num_workers=0表示只有主进程去加载batch数据,这个可能会是一个瓶颈。
•num_workers = 1表示只有一个worker进程用来加载batch数据,而主进程是不参与数据加载的。这样速度也会很慢。
•num_workers>0 表示只有指定数量的worker进程去加载数据,主进程不参与。增加num_works也同时会增加cpu内存的消耗。所以num_workers的值依赖于 batch size和机器性能。
•一般开始是将num_workers设置为等于计算机上的CPU数量
•最好的办法是缓慢增加num_workers,直到训练速度不再提高,就停止增加num_workers的值。