数据结构 -- 跳跃链表

news2024/11/28 14:17:08

跳跃链表的概念

跳跃链表是有序链表的一个变种，在一个有序链表中，查找一个链表中的元素需要进行一次遍历，时间复杂度为O(n)，为了加快查找的过程，能够跳过某些元素呢？一个思路就是牺牲一定的空间换时间，对有序链表建立类似索引的结构加快查找过程，跳跃链表基本上就是通过维护一个多层次的链表，每一层链表中的元素是前一层链表元素的子集，搜索时，最开始在最稀疏的层次进行搜索，直至需要查找的元素在该层两个相邻元素中间，这时，将跳转到下一个层次，重复刚才的搜索，直到找到需要查找的元素为止。

跳跃链表的创建

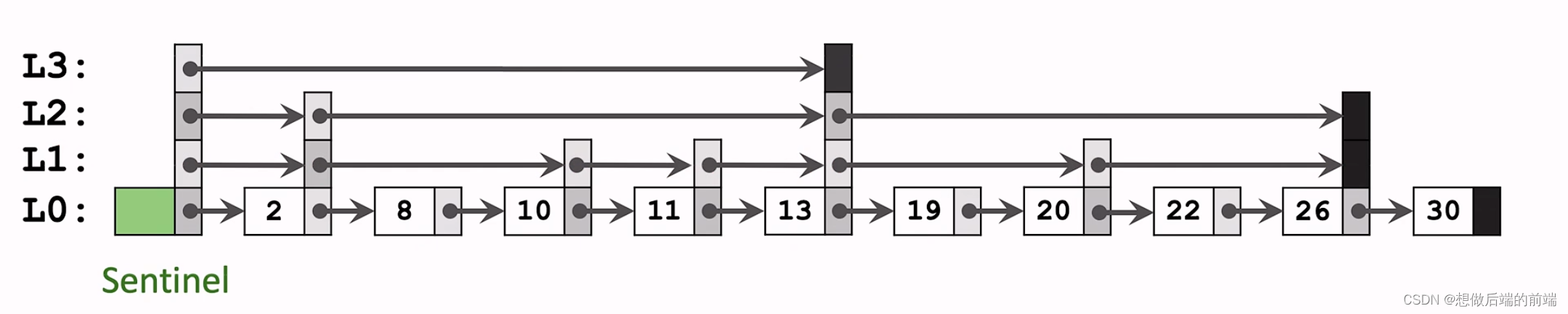
在这里插入图片描述
如果给定一个固定的有序链表，构造跳跃链表的话，思路非常简单，就是每一层都取上一层的1/2个元素就可以了（例如，按奇偶，每次都取第偶数个元素作为下一层元素…），这样查找就相当于二分查找的过程，查找一个元素的时间复杂度变为了log(n)。但是实际应用中，有序链表往往不是固定元素个数的，会动态的增删，这种静态的构建过程就不合适了，那该怎么办呢？

可以看到，跳跃链表构建索引的关键是每一层都取上一层的部分元素作为该层的元素，即第i层的元素按某个固定的概率p（例如1/2或1/4）出现在第i+1层中。可通过这个概率p值对空间和时间进行平衡，p越大，占用空间越多。所以，构建的思路就是在插入一个新的元素时，随机的生成该元素的层数，算法描述如下：

randomLevel()
    lvl := 1
    // random() return a random value in [0..1) 
    while random() < p && lvl < MaxLevel do
        lvl := lvl + 1
    return lvl

即，层次越高，概率越低，但层数也不能太高，太高了无意义，一般根据元素的个数n计算MaxLevel = log(n)作为最高层数。这样，跳跃链表就适应动态变化的情况了。

跳跃链表的插入、查找、删除

查找

查找的思路就是先在最上层查找，找到不到再转向下一层继续查找，这样就可以跳过很多元素，缩小查找范围。
比如寻找key =20:
第一步：从L3出发，找到第一个节点13，因为13是L3的最后一个节点了，所以向下寻找；
在这里插入图片描述
第二步：因为20>13，所以到L2后往右出发，找到L2的第二个节点26，并且26为L2的最后一个节点，所以继续向下寻找；
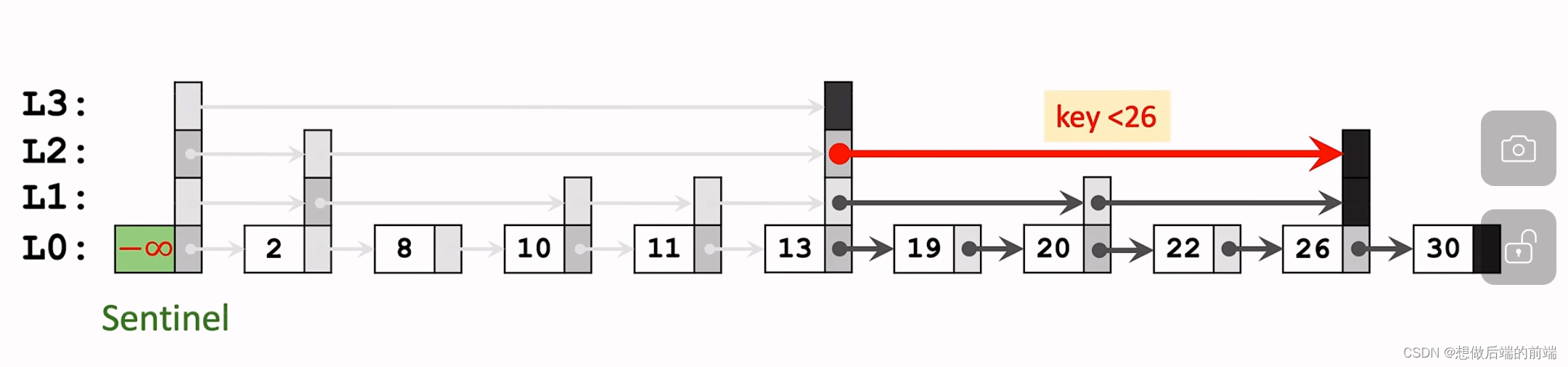
在这里插入图片描述
第三步：因为26>20所以在L1中我们继续从节点13开始向右寻找，找到下一个节点即为20
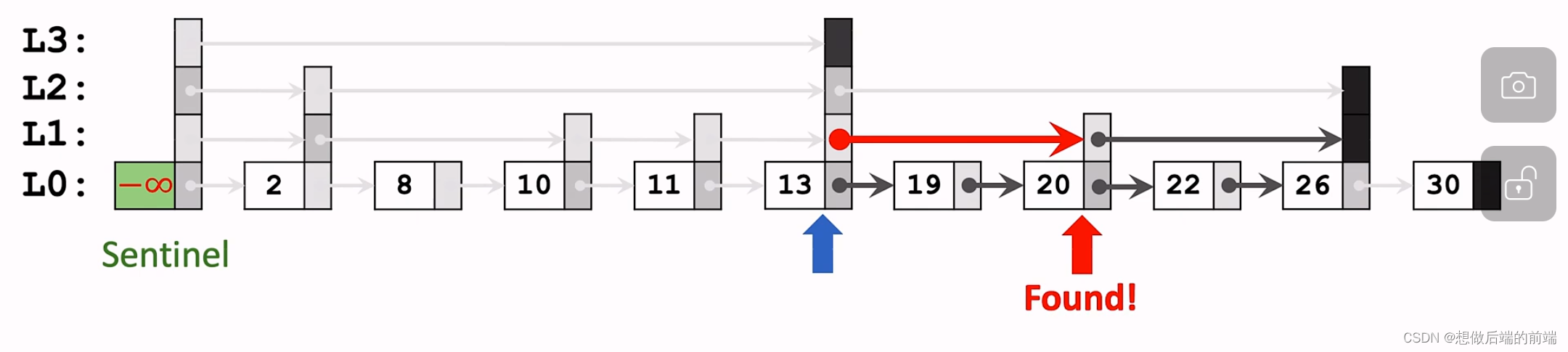
在这里插入图片描述
算法描述如下：

Search(list, searchKey)
    x := list->header  // loop invariant: x->key < searchKey
    for i := list->level downto 1 do    // downto的意思是从最高层，每次下降一层
        while x->forward[i]->key < searchKey do
            x := x->forward[i]  // x->key < searchKey <= x->forward[1]->key
    x := x->forward[1]
    if x->key = searchKey then return x->value
        else return failure

插入

插入的关键步骤是随机决定节点层数，算法前面已经描述过，与普通链表不同的是跳跃链表是多层的，所以确定层数后每一层都需要插入该元素。
比如插入key =9:
第一步：查找key=9的位置，并且记录下位置
在这里插入图片描述
第二步：创建一个新的节点，它的高度是随机算法生成的的，然后把节点插入到跳跃链表中
在这里插入图片描述
第三步：将新的节点与跳跃链表连接起来
在这里插入图片描述

算法描述如下：

Insert(list, searchKey, newValue)
    local update[1.. MaxLevel]
    x := list->leader
    for i:= list->level downto 1 do
        while x->forward[i]->key < searchKey do
            x := x->forward[i]  // x->key < searchKey <= x->forward[1]->key
        update[i] := x  //这里是找出这个元素在每一层的前驱节点
    x := x->forward[1]
    if x->key = searchKey then x->value := newValue
    else
        lvl := randomLevel()
        if lvl > list->level then
            for i := list->level + 1 to lvl do
                update[i] := list->header
            list->level := lvl
        x := makeNode(lvl, searchKey, value)
        for i := 1 to level do  // 这里与普通链表插入节点操作类似，只不过是每层都要插入
            x->forward[i] := update[i]->forward[i]
            update[i]->forward[i] := x

删除

删除操作与普通链表删除操作类似，不同的地方在于找到该元素后要每一层都做删除操作，算法描述如下：

Delete(list, searchKey)
    local update[1..MaxLevel]
    x := list->header
    for i := list->level downto 1 do
        while x->forward[i]->key < searchKey do
            x := x->forward[i]
        update[i] := x
    x := x->forward[1]
    if x->key = searchKey then
        for i := 1 to list->level do
            if update[i]->forward[i] neq x then break
            update[i]->forward[i] := x->foreard[i]
        free(x)
        while list->level > 1 and list->header->forward[list->level] =NIL do 
            list->level := list->level -1

完整算法

#include<iostream>
#include<cstdlib>
#include<ctime>
#include<random>
#include<cmath>
#include<climits>
#include<vector>
#include<cassert>
#include<algorithm>

using namespace std;

const int MAX_LEVEL = 8;   // 用户定义的最大层数
const float P = 0.5;        // 用户设置的概率P

//跳跃列表节点类
template<class K, class V>
class SkipListNode {
public:
    SkipListNode() {}
    SkipListNode(K key, V value, int level);
    K key;
    V value;
    typedef SkipListNode<K, V>* NodePtr;
    NodePtr forward[MAX_LEVEL];
};

template<class K, class V>
SkipListNode<K, V>::SkipListNode(K key, V value, int level):key(key),value(value) {
    for (int i = 0; i < level; ++i) {
        this->forward[i] = nullptr;
    }
}

// 跳跃列表类
template<class K, class V>
class SkipList {
public:
typedef SkipListNode<K, V>* NodePtr;

    SkipList();
    SkipList(NodePtr header, NodePtr tail);
    ~SkipList();
    V* search(const K& key);
    void insert(const K& key,const V& value);
    void remove(const K& key);
    void print();
private:
    int randomLevel() const;
    NodePtr header;           // header节点
    NodePtr tail;             // tail节点
    int level;                // 当前层数
    int n;                    // 节点数量
};

template<class K, class V>
void SkipList<K, V>::print() {
    assert(this->header != nullptr);
    std::cout << "level=" << this->level << " count=" << this->n << endl;
    for (int i = this->level - 1; i >= 0 ; --i) {
        cout << "level" << i + 1 << ":";
        NodePtr pNode = this->header->forward[i];
        while (pNode != this->tail) {
            cout << "<" << pNode->key << ", " << pNode->value << ">  ";
            pNode = pNode->forward[i]; 
        }
        cout << endl;
    }
}

template<class K, class V>
SkipList<K, V>::SkipList() {
    this->header = nullptr;
    this->tail = nullptr;
    this->level = 0;
    this->n = 0;
}

template<class K, class V>
SkipList<K, V>::SkipList(NodePtr header, NodePtr tail) {
    this->header = header;
    this->tail = tail;
    this->level = 1;
    this->n = 0;
    for (int i = 0; i < MAX_LEVEL; ++i) {
        this->header->forward[i] = tail;
    }
}

template<class K, class V>
SkipList<K, V>::~SkipList() {
    NodePtr p = this->header;
    while (p->forward[0] != nullptr) {
        NodePtr tmp = p;
        p = p->forward[0];
        delete tmp;
    }
}

template<class K, class V>
int SkipList<K, V>::randomLevel() const {
    int lvl = 1;
    int maxLevel = (int)log(this->n) + 1;
    while (rand() % 100 < P * 100 && lvl < min(maxLevel, MAX_LEVEL)) {
        ++lvl;
    }

    return lvl;
}

template<class K, class V>
V* SkipList<K, V>::search(const K& key) {
    NodePtr x = this->header;
    for (int i = 0; i < this->level; ++i) {
        while (x->forward[i]->key < key) {
            x = x->forward[i];
        }
    }

    x = x->forward[0];      
    if (x->key == key) {
        return &x->value;
    } else {
        return nullptr;
    }
}

template<class K, class V>
void SkipList<K, V>::insert(const K& key,const V& value) {
    // 找到待调整的项
    NodePtr update[MAX_LEVEL];
    NodePtr ptr = this->header;
    for (int i = this->level - 1; i >= 0; --i) {
        while (ptr->forward[i]->key < key) {
            ptr = ptr->forward[i];
        }
        update[i] = ptr;
    }

    if (update[0]->forward[0]->key == key) {
        update[0]->forward[0]->value = value;
        return;
    }
    // 进行节点加入操作（与链表插入类似）
    const int lvl = this->randomLevel();        // 随机生成该节点层数
    if (lvl > this->level) {
        for (int i = this->level; i< lvl; ++i) {
            update[i] = this->header;
        }
        this->level = lvl;
    }

    NodePtr x = new SkipListNode<K, V>(key, value, lvl);
    for (int i = 0; i < this->level; ++i) {
        x->forward[i] = update[i]->forward[i];
        update[i]->forward[i] = x;
    }

    this->n++;
}

template<class K, class V>
void SkipList<K, V>::remove(const K& key) {
    NodePtr update[MAX_LEVEL];
    NodePtr x = this->header;
    for (int i = this->level -1; i >= 0; --i) {
        while (x->forward[i]->key < key) {
            x = x->forward[i];
        }
        update[i] = x;
    }

    x = x->forward[0];
    if (x->key == key) {
        for (int i = 0; i < this->level; ++i) {
            if (update[i]->forward[i] != x) 
                break;
            update[i]->forward[i] = x->forward[i];
        }
        delete x;
        this->n--;
        while (this->level > 1 && this->header->forward[this->level - 1] == this->tail) {
            this->level--;
        }
    }
} 

int main() {
    srand(time(nullptr));
    SkipListNode<int, int> *header = new SkipListNode<int, int>(INT_MIN, 0, 1);
    SkipListNode<int, int> *tail = new SkipListNode<int, int>(INT_MAX, 0, 1);
    SkipList<int, int>* pSkiplist = new SkipList<int, int>(header, tail);
    pSkiplist->insert(10, 10);
    pSkiplist->insert(15, 15);
    pSkiplist->insert(12, 12);
    pSkiplist->insert(18, 18);
    pSkiplist->insert(1, 1);
    pSkiplist->insert(121, 121);
    pSkiplist->insert(118, 118);
    pSkiplist->insert(10, 100);
    pSkiplist->print();
    int* v = pSkiplist->search(121);
    cout << "value is :" << *v << endl;
    pSkiplist->remove(118);
    pSkiplist->print();
    pSkiplist->insert(11860, 1180);
    pSkiplist->insert(11850, 1180);
    pSkiplist->insert(11840, 1180);
    pSkiplist->insert(11830, 1180);
    pSkiplist->insert(11820, 1180);

    pSkiplist->print();

    delete pSkiplist;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/620349.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

入职外包一个月，我离职了

入职外包一个月，我离职了

有一种打工人的羡慕&#xff0c;叫做“大厂”。 真是年少不知大厂香&#xff0c;错把青春插稻秧。 但是&#xff0c;在深圳有一群比大厂员工更庞大的群体&#xff0c;他们顶着大厂的“名”&#xff0c;做着大厂的工作&#xff0c;还可以享受大厂的伙食&#xff0c;却没有大厂…
阅读更多...
Redis系列第一篇：ubuntu18.04下源码编译安装Redis 6.2.12

Redis系列第一篇：ubuntu18.04下源码编译安装Redis 6.2.12

Redis&#xff08;Remote Dictionary Server )&#xff0c;即远程字典服务&#xff0c;是一个开源的使用ANSI C语言编写、支持网络、可基于内存亦可持久化的日志型、Key-Value数据库&#xff0c;并提供多种语言的API。 Redis是一个key-value存储系统。和Memcached类似&#xff…
阅读更多...
EasyExcel设置动态head数据(不是格式)及postman自测的坑

EasyExcel设置动态head数据(不是格式)及postman自测的坑

需求背景&#xff1a; 导出某某业务模块的数据&#xff0c;但是&#xff0c;数据列的标题内容是根据当前日期计算出来的。 比如今天是5月20&#xff0c;那么列就是 5/21 、 5/22…以此类推 问题&#xff1a; EasyExcel 通过Bean的注解实现匹配的&#xff0c;这是最便捷的方式&…
阅读更多...
这5款小众又好用的软件，你都知道吗？

这5款小众又好用的软件，你都知道吗？

1.文件比较——WinMerge WinMerge是一款用于比较和合并文件和文件夹的工具。它可以让你对不同的文件和文件夹进行可视化的对比,并显示出差异和相似之处。WinMerge支持多种功能,如合并,同步,过滤,插件等。这款工具非常实用,但是可以提供强大的文件比较功能,是管理文件和解决冲突…
阅读更多...
123 2021年国赛 二分搜索+前缀和

123 2021年国赛 二分搜索+前缀和

题目描述 小蓝发现了一个有趣的数列&#xff0c;这个数列的前几项如下&#xff1a; 1, 1, 2, 1, 2, 3, 1, 2, 3, 4, 小蓝发现&#xff0c;这个数列前 1 项是整数 1&#xff0c;接下来 2 项是整数 1 至 2&#xff0c;接下来 3 项是整数 1 至 3&#xff0c;接下来 4 项是整数…
阅读更多...
day2 ARM处理器概论

day2 ARM处理器概论

目录 RISC处理器和CISC处理器 SOC(System on Chip) ARM指令集概述 指令集 ARM指令集 编译原理 ARM存储模型 ARM指令存储 ARM工作模式 工作模式的理解 ARM工作模式分类 RISC处理器和CISC处理器 RISC处理器 只保留常用的的简单指令&#xff0c;硬件结构简单&#xff0c;复…
阅读更多...
你觉得你很优秀，为什么连一个软件测试面试都过不了？

你觉得你很优秀，为什么连一个软件测试面试都过不了？

目录 前言 简历请用数字化结果不要只是堆研工作经历 简历一:我的工作内容有 简历二:我的工作内容有: 当你和HR面对面坐下来时&#xff0c;迎接我们的第一个问题往往是:“来&#xff0c;请简单介绍下你自己吧。 了解你的过去是判断你未来的最好方式 增加好印象&#xff0c…
阅读更多...
基于SVM的鸢尾花数据集回归分析

基于SVM的鸢尾花数据集回归分析

目录 1. 作者介绍2. SVM支持向量机算法2.1 鸢尾花数据集2.2 鸢尾花数据集可视化2.2.1 散点图2.2.2 箱型图2.2.3 三维散点图&#xff08;3D&#xff09; 3. SVM算法实现3.1 完整代码3.2 运行结果3.3 问题与分析 1. 作者介绍 张佳伦&#xff0c;男&#xff0c;西安工程大学电子信…
阅读更多...
androidstudio ffmpeg 音频转换

androidstudio ffmpeg 音频转换

java-ffmpeg-音频转换 需求描述功能流程所需条件步骤步骤1步骤2步骤3一些我使用中遇到的异常 需求描述 项目中的语音唤醒后的语音识别人声检测一直是一个很令我头痛的问题,之前因为对各种类型的工具包使用不熟练,以及时间问题,一直没有根治这个人声检测体验不好的问题,之前的解…
阅读更多...
不同品牌或型号的单片机

不同品牌或型号的单片机

以下是一些常见的单片机品牌和型号&#xff1a; 微控制器&#xff08;Microchip&#xff09;&#xff1a;PIC系列&#xff08;如PIC16F877A、PIC18F4550&#xff09; 瑞萨电子&#xff08;Renesas&#xff09;&#xff1a;RX系列&#xff08;如RX231、RX65N&#xff09;需要资…
阅读更多...
Termius 最好用的SSH 连接工具

Termius 最好用的SSH 连接工具

Termius 最好用的SSH 连接工具 一、环境准备二、配置2.1 terminus 安装2.2 删除自动更新2.3 修改用户信息 三、使用四、页面展示 该工具 mac os 可直接使用 本文只展示 windows 使用步骤&#xff0c;本教程使用的 termius 版本为 7.59.6 一、环境准备 termius 下载 官网下载地址…
阅读更多...
ubuntu上安装docker报错

ubuntu上安装docker报错

执行docker命令的时候报错如下&#xff1a; Cannot connect to the Docker daemon at unix:///var/run/docker.sock. Is the docker daemon running? 为了解决这个问题&#xff0c;看了一些帖子有的说重启docker.service服务或者看该服务是否已经正常启动&#xff0c;结果网上…
阅读更多...
超实用！新手项目经理掏心窝总结的经验

超实用！新手项目经理掏心窝总结的经验

像项目这样复杂的环境中&#xff0c;往往会出现错误判断、沟通不畅、管理不善以及最常见的错误。因此&#xff0c;项目管理需要项目经理有广泛的经验、洞察力和技能&#xff0c;无论是规划、组织还是有效领导团队&#xff0c;以在规定的时间和预算内实现项目目标。在这种情况下…
阅读更多...
基于BAT指令定时备份Oracle并发送邮件

基于BAT指令定时备份Oracle并发送邮件

前言 在企业级应用程序中&#xff0c;数据是非常重要的资源。因此&#xff0c;我们需要定期备份数据以确保其安全性和完整性。在Oracle数据库中&#xff0c;我们可以使用多种方法来备份数据&#xff0c;其中一种方法是使用BAT脚本来进行自动化备份。 在本文中&#xff0c;我们…
阅读更多...
【AI实时变声器，声音甜甜的小姐姐背后竟是抠脚大汉】

【AI实时变声器，声音甜甜的小姐姐背后竟是抠脚大汉】

前言 这是一款基于AI算法的实时变声器&#xff0c;如果你不懂AI也没事&#xff0c;直接使用我提供的一键安装包 链接&#xff1a;https://pan.baidu.com/s/1f3X6JdBVOgeTNPf0B3CRKg 提取码&#xff1a;k5v2 变声器安装使用 有两款变声器&#xff0c;都是基于RVC做的&#xf…
阅读更多...
ctfshow——web入门 SSRF

ctfshow——web入门 SSRF

web351web352web353web354web355web356web357web358web359web360 web351 通过hackbar post提交 urlhttp://127.0.0.1/flag.php 获得flag web352 将127.0.0.1和localhost给过滤了&#xff0c;但并不影响post提交 post urlhttp://127.0.0.1/flag.php web353 过滤了localhost和1…
阅读更多...
python基础学习1

python基础学习1

pyhton数据分析的优势&#xff1a; ①语法简单精炼 ②有很强大的库 ③功能强大 ④适用于构建生产系统 ⑤胶水语言 python数据分析常用的类库&#xff1a; ①IPython------科学计算标准工具集的组成部分 ②NumPy------python科学计算的基础包 ③SciPy--------解…
阅读更多...
【手撕Spring源码】深度理解SpringBoot

【手撕Spring源码】深度理解SpringBoot

文章目录 Tomcat内嵌容器Tomcat 基本结构创建Tomcat内嵌容器内嵌Tomcat集成Spring 容器 Boot 自动配置什么是自动配置类自动配置类原理Aop自动配置DataSource自动配置MyBatis自动配置事务自动配置MVC自动配置条件装配 附&#xff1a;注解小总EnableConfigurationPropertiesCond…
阅读更多...
RWKV配上ChatGPTBox让我们在浏览器中感受AI带来的魅力

RWKV配上ChatGPTBox让我们在浏览器中感受AI带来的魅力

这次我们来讲讲RWKV搭配ChatGPTBox结合使用带来的功能体验&#xff0c;这两个项目都是同一个大神创建的&#xff0c;完全可以无缝搭配进行使用。 以下是我之前在本地部署了AI模型RWKV的教程&#xff0c;如果还没有本地部署过AI的童鞋可以查看我之前发布的教程&#xff0c;在自…
阅读更多...
在线聊天项目

在线聊天项目

人事管理项目-在线聊天 后端接口实现前端实现 在线聊天是一个为了方便HR进行快速沟通提高工作效率而开发的功能&#xff0c;考虑到一个公司中的HR并不多&#xff0c;并发量不大&#xff0c;因此这里直接使用最基本的WebSocket来完成该功能。 后端接口实现 要使用WebSocket&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023