前面已经给出了线性调频信号的时域表达形式，并介绍了信号的实部、虚部、相位、频率等，本文介绍线性调频信号的频谱，以及推导线性调频信号时常用的驻定相位原理。计算信号的频谱，实际上就是对信号做傅里叶变换。即 

 

         驻定相位原理认为，对于一个时域快速变化的信号，除了导数为零的位置（驻留点）外，其余区域的正负面积几乎为0，可以相互抵消，最终函数的积分结果主要受驻留点区域的影响。

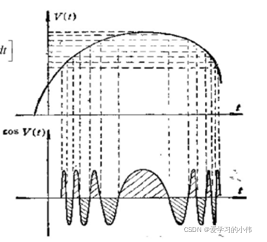
        以下图所示的信号为例，假设慢时间信号U(t) 如上图所示，快时间信号cosVt 如下图所示，计算积分 时，由于 的正部分与负部分相互抵消，积分结果接近0，只有在驻留点处，由于相位变换率很小，相位值有很长时间的滞留，才使得积分结果不为0。

仍然以chirp信号为例，前面已经得到了驻留点为

 

clear;clc;close all;

Tr = 10e-6;          
Br = 60e6;            
Kr = Br/Tr;                   
Fs = 66.666667e6;
Ts = 1/Fs;             
N = 2048;
N = floor(Fs*Tr/2)*2;
tr = [-N/2:N/2-1]/Fs;
fr = [-N/2:N/2-1]/N*Fs;

%%
st = (abs(tr)<Tr/2).*exp(j*pi*Kr*tr.^2);
Sf = fft(st);

figure, 
subplot(221), plot(fr*1e-6, real(Sf)), grid on, 
xlabel('time (us)'); 
title('频谱实部')
subplot(222), plot(fr*1e-6, imag(Sf)), grid on, 
xlabel('time (us)'); 
title('频谱虚部')
subplot(223), plot(fr*1e-6, abs(fftshift(Sf))), grid on, 
xlabel('frequency (MHz)'); 
title('信号频谱');
subplot(224), plot(fr*1e-6, unwrap((angle((Sf))))), grid on, 
xlabel('frequency (MHz)');  ylabel('phase (rad)') 
title('频谱相位');

程序运行的结果如下图所示。

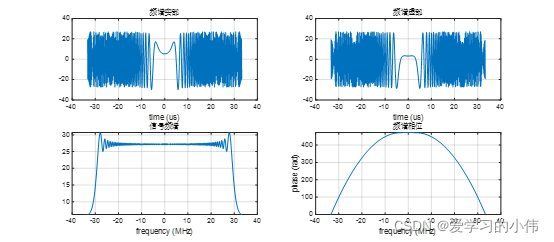
 可以看出：

• 频谱的实部和虚部具有与LFM信号相似的线性调频结构，与LFM不同的是，频谱存在π/4 的相位，且调频率符号发生了变化。
• 频谱的幅度也可以近似为一个rect函数，由于Fs>Br，所以幅度谱存在一个跳变。
• 频谱的相位与LFM信号的相位基本一致，也可以近似为一个关于频域的二次函数，说明LFM信号的频率与时间之间存在意义对应的线性关系。

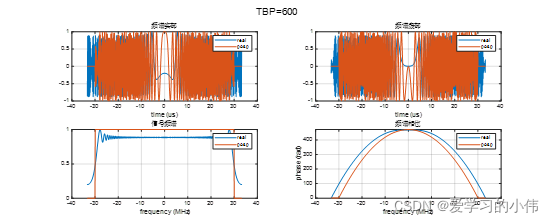
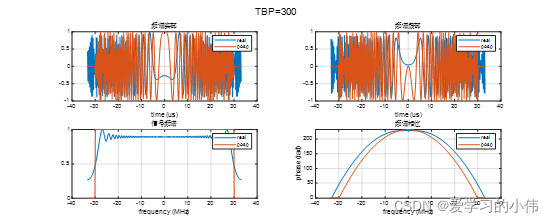
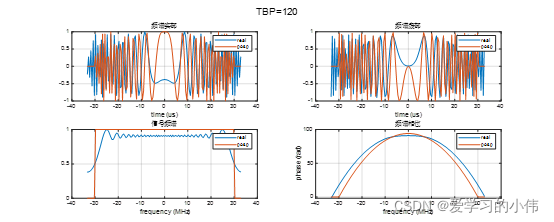
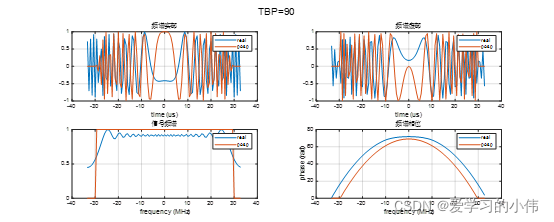
        在计算LFM信号的频谱时，驻定相位原理得到的结果只是一种近似，但是这种近似在TBP>100时精度非常高，可以满足SAR成像处理的要求。下图给出了不同TBP下，LFM信号的频谱，其中蓝线是频谱的真实值，橙线为使用驻定相位原理计算的理论值。