在了解 Tarjan 算法之前，我们先来了解 dfs 搜索树。

1 dfs 生成树

定义： dfs 遍历整张图，按照 dfs 序构成一棵树。

1.1 有向图的 dfs 生成树

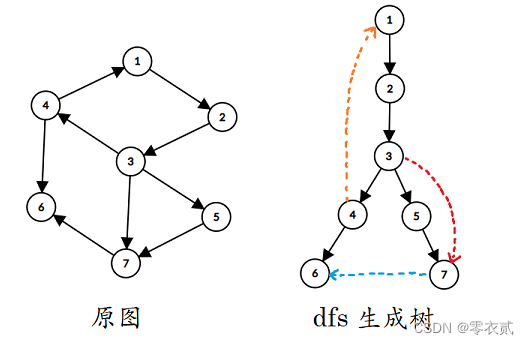
有向图的 dfs 生成树包括四种边：

• 树边（tree edge）：图中黑色边表示。表示搜索访问到未访问过的结点。
• 回边（back edge）：图中橙色边表示。表示该边指向先前访问过的祖先。
• 叉边（cross edge）：图中蓝色边表示。表示该边指向先前访问过的非祖先结点。
• 前向边（forward edge）：图中红色边表示。表示该边指向先前访问过的孩子结点。

1.2 无向图的 dfs 生成树

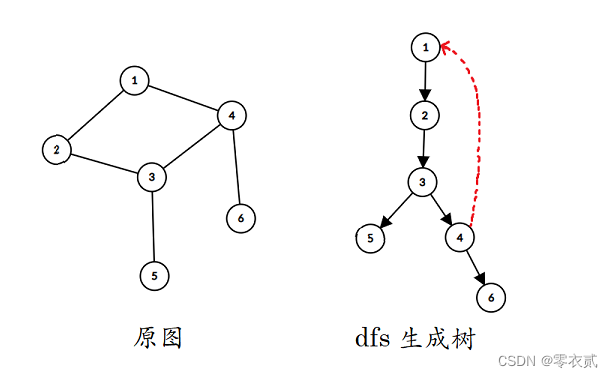
无向图的 dfs 生成树仅包含两种边：树边和回边。

证明没有叉边和前向边：

• 如果存在叉边 $u\to v$，其中 $u$ 为当前搜索访问到的结点， $v$ 为之前访问过的非祖先结点，那么在访问 $v$ 时，就应该访问了 $u$，与 $u$ 为当前搜索访问到的结点矛盾。

• 如果存在前向边 $u\to v$ ，那么在首次访问 $v$ 时，该边就会作为一条回边指向 $u$ ，不会作为 $u\to v$ 一条前向边。

---

2 Tarjan 算法

2.1 桥

题目

2.1.1 桥的定义

无向图中，若删去一条边会使得这个图的极大连通分量数增加，则该边被称为桥。

也可以理解为无向图的一个连通块中，若删除一条边会使得至少两点之间无法相互到达，该边被称为桥。

2.1.2 实现

样例：

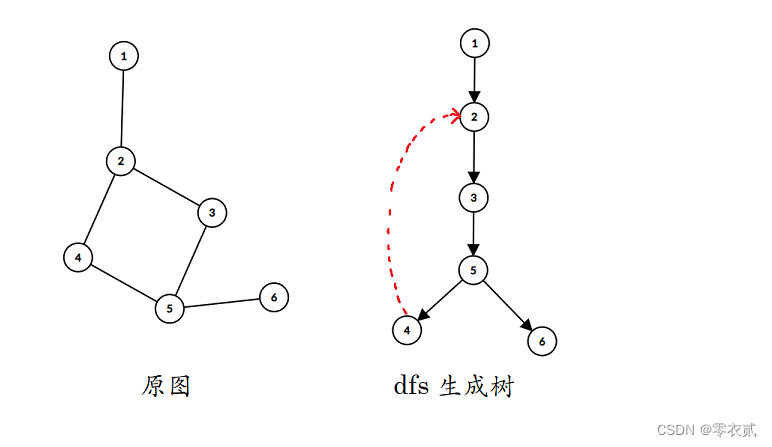
样例中，$1\to 2$ 和 $5\to 6$ 就是该图的桥。

• 容易发现，只有 树边 才可能作为桥，而 dfs 生成树中红色的回边 $4\to 2$ 标记了 $2\to 3\to 5\to 4$ 沿途上的树边都不可能作为桥。因此我们得出结论：一条边是桥，当且仅当它是 不被回边标记的树边。

在 Tarjan 算法中，我们对每个点 $u$ 按 dfs 序打上时间戳 $df{n}_u$，同时记录 $lo{w}_u$ 表示 $u$ 不经过其父亲能到达的最小时间戳，即按照 dfs 生成树中有向边能到达的最小时间戳。

那么一条树边 $u\to v$ 不被回边标记的充要条件即为：$lo{w}_v>df{n}_u$。如例中，$1\to 2$，low[2]=2,dfn[1]=1，可以得到 $1\to 2$ 就是一座桥。

void Tarjan(int u, int fa)
{
	dfn[u] = low[u] = ++ idx;
	for(auto v : G[u])
	{
		if(v == fa) continue;
		
		if(!dfn[v]) // tree edge 
		{
			Tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(low[v] > dfn[u]) // is bridge
				bridge[u][v] = 1;
		}
		
		else // back edge 
			low[u] = min(low[u], dfn[v]);
	}
}

2.2 割点

题目

2.2.1 割点的定义

无向图中，若删去一个点会使得这个图的极大连通分量数增加，这个点被称为割点。

也可以理解为无向图的一个连通块中，若删除一个点会使得至少两点之间无法相互到达，该点被称为割点。

2.2.2 实现

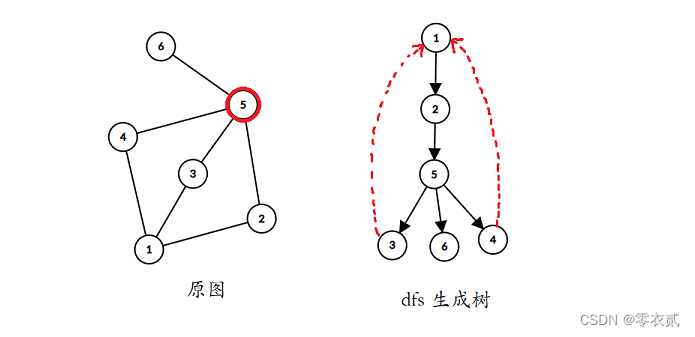
首先，由于图不连通，我们大体的决策是将图分成若干连通块，在每个连通块对应的 dfs 生成树上进行搜索。

• 对于结点 $5$，删去 $5$ 显然不会对儿子结点 $3,4$ 造成影响，因为它们有回边可以连到结点 $5$ 的祖先，而对于儿子结点 $6$ 会有影响，其没有回边可以连到可以连到结点 $5$ 的祖先。

  我们推广到一般情况：对于结点 $u$ ，若存在儿子结点的 $lo{w}_v\ge df{n}_u$ ，即 $v$ 没有回边可以连到结点 $u$ 的祖先，那么 $u$ 一定是个割点。

• 然而 $1$ 号虽然满足上述条件，然而 $1$ 并不是割点。

  因此我们还需判断一种情况，即 $u$ 作为了 dfs 搜索树的根节点，不论如何其任何儿子 $v$ 的 $lo{w}_v$ 都不可能小于 $df{n}_u$ ，因此需要分开讨论：当 $u$ 作为根节点时，若 $u$ 有两个及以上的儿子时，$u$ 为割点。

int dfn[N], low[N], idx, cnt;
bool cut[N];
void Tarjan(int u, int fa)
{
	dfn[u] = low[u] = ++ idx;
	
	int son = 0;
	
	for(auto v : G[u])
	{	
		if(v == fa) continue;
		
		if(!dfn[v])
		{	
			Tarjan(v, u);
			low[u] = min(low[u], low[v]);
			
			son ++ ;
			if(fa != 0 and low[v] >= dfn[u] and !cut[u]) cnt ++ , cut[u] = 1;
		}
		
		else low[u] = min(low[u], dfn[v]);
	}
	
	if(fa == 0 and son >= 2 and !cut[u]) cnt ++ , cut[u] = 1;
	
}

代码

2.3 强连通分量

题目

2.3.1 强连通分量的定义

注意，强连通分量（SCC，Strongly Connected Components）是在单向图中的。

强联通子图，定义为：在 单向图 中，该子图上的任意两点之间能互相到达。

强联通分量，定义为： 极大连通子图。

2.3.2 实现

以下图为例：

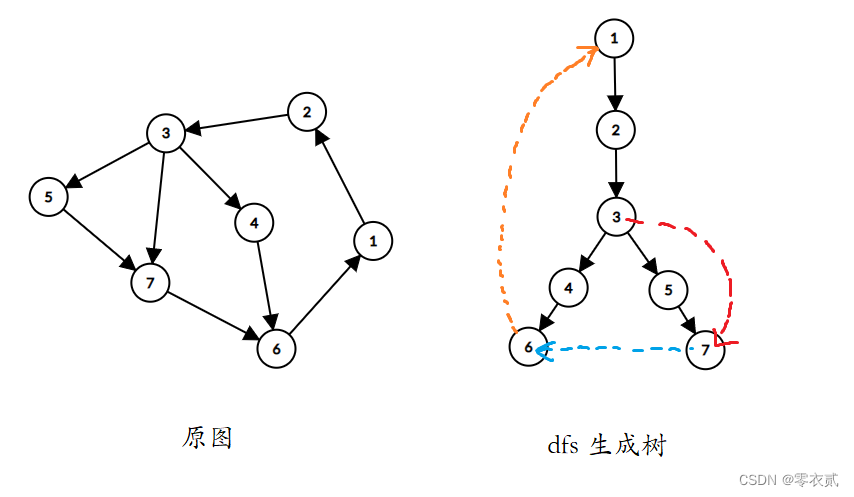
该例中强连通分量为 $1,2,3,4,5,6,7$ 。

• 若 $u$ 是当前 scc 第一个被访问的结点，那么该 scc 的结点一定在 dfs 生成树中以 $u$ 为根的子树内。

  若存在该 scc 中的 $v$ 不在子树内，则 $u$ 到 $v$ 的路径中一定存在叉边或回边，根据叉边、回边的定义，则 $v$ 在 $u$ 之前已经被访问过，与 $u$ 是当前 scc 第一个被访问的结点矛盾。

• 如果我们把单个节点也算作是强连通分量，那么所有 scc 的根应 $u$ 当都满足 $lo{w}_u=df{n}_u$ 。

具体实现

考虑使用一个栈 $s$ 存储遍历到的结点，每当访问到一个 $lo{w}_u=df{n}_u$ 的结点，就将栈内元素从栈顶 弹出直至 $u$ ，这些结点即为以 $u$ 为根的强连通分量。

在遍历 $u$ 的子树过程中，确实有可能会遍历到其他强连通分量的点，根据树的结构，一定会先遍历到其他 scc 的根 $v$，而在遍历 $v$ 的过程中，发现了 $lo{w}_v=df{n}_v$ ，便会将栈内的元素弹出直到 $v$，因此在遍历完 $u$ 的子树后仍然留在栈中的元素一定是以 $u$ 为根的 scc 中的元素。

而在搜索过程中，我们会遍历到以下三种结点：

• 未访问的结点：该边为树边，将 $v$ 入栈，对 $v$ 进行 dfs，更新 $low$ 。

• 访问过并且不在栈中：该边为叉边或前向边，说明已经是其他 scc 中的结点，对当前 scc 不会产生任何影响，忽略。

• 访问过并且在栈中：该边为叉边、前向边或回边，更新 $low$ 值。

int low[N], dfn[N], idx;
bool ins[N];
int tot, belong[N];

stack <int> s;

void Tarjan(int u)
{
	low[u] = dfn[u] = ++ idx;
	
	s.push(u); ins[u] = 1;
	
	for(auto v : G[u])
	{
		if(!dfn[v])
		{
			Tarjan(v);
			low[u] = min(low[u], low[v]);
		}
		if(dfn[v] and ins[v]) 
			low[u] = min(low[u], dfn[v]);
	}
	
	if(low[u] == dfn[u]) // 当前 scc 的根
	{
		++ tot;
		while(s.top() != u) // 出栈，标记结点所属 scc
		{
			int x = s.top(); s.pop();
			belong[x] = tot, ins[x] = 0;
		}
		s.pop(); belong[u] = tot, ins[u] = 0;
	}
	
}

代码

2.3.3 强连通分量缩点

在无向图的一些问题中，若将所有 scc 合并为一个点，那么这张无向图就会变成一张有向无环图（DAG，Directed Acyclic Graph）。

因此我们只需保留连接两个不同 scc 的边来构成缩点后的新图。

	for(int i=1; i<=n; i++)
	{
		if(!dfn[i])
			idx = 0, Tarjan(i);
	}
	
	for(int u=1; u<=n; u++) // 缩点后的图 e
	{
		for(auto v : G[u])
		{
			int x = belong[u], y = belong[v];
			if(x != y)
				e[x].push_back(y);
		}
	}

[模板] 缩点

题目

由于题目存在环且能多次经过同一点，直接在图上进行搜索显然不可行。

由于点权均为非负数，在经过一个环时，显然应当经过还上的所有点，此时我们考虑缩点，将图变成一张 DAG ，然后用记忆化搜索或者拓扑排序求解最长路径即可。

2.4 双联通分量

无向图中，双联通分量包含点 点双联通分量、边双联通分量。

2.4.1 双联通分量的定义

• 点双联通：对于点 $u$ 和 $v$ ，删去图上任意一个点，$u$ 和 $v$ 始终连通，则称 $u$ 和 $v$ 点双联通。

  容易发现，若一个子图点双连通，那么这个子图上一定不存在割点。

• 边双连通：对于点 $u$ 和 $v$ ，删去图上任意一条边，$u$ 和 $v$ 始终连通，则称 $u$ 和 $v$ 双联通。

  容易发现，若一个子图边双连通，那么这个子图上一定不存在桥。

• 点双连通分量：极大点双连通子图。

• 边双连通分量：极大边双连通子图。

2.4.2 边双的实现

题目

在找出原图上的桥后，将其在原图中去掉，剩下的连通块即为边双连通分量。

int cnt; 
bool vis[N];
vector <int> dcc[N];
void dfs(int u)
{
	vis[u] = 1;
	dcc[cnt].push_back(u);
	for(int i=head[u]; i; i=e[i].nxt)
	{
		if(vis[e[i].v] or bridge[i]) continue;
		dfs(e[i].v);
	}
}

代码

2.4.3 边双缩点

我们将每个边双看作一个新节点，原图上的桥看作连接边双之间的边，这样新图会构成一棵树。

for(int i=2; i<=tot1; i++)
	{
		int u = e1[i].v, v = e1[i ^ 1].v;
		int x = belong[u], y = belong[v];
		if(x != y) add_edge2(x, y);
	}

[NOIP2022] 建造军营

题目

在边双中的任意两点之间都不需要保护道路，考虑边双缩点。由于原图为连通图，边双缩点后变为一棵树，进行树 dp 统计答案。

2.4.4 点双的实现

详见圆方树章节。