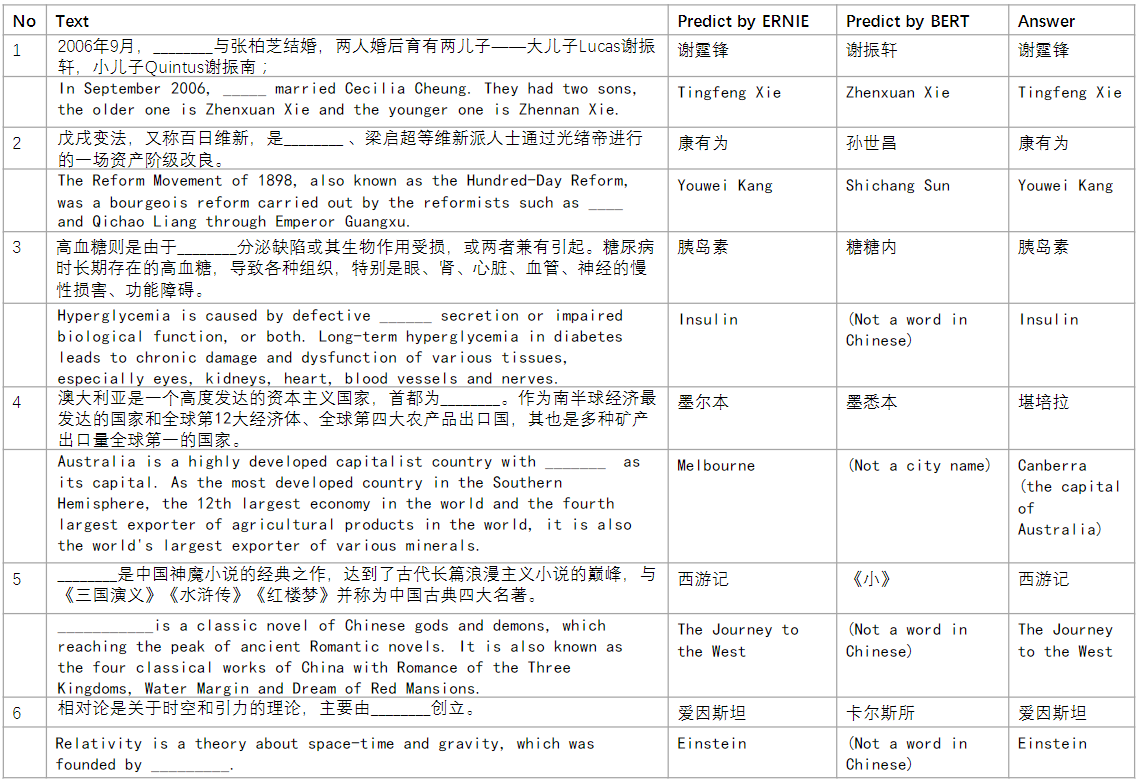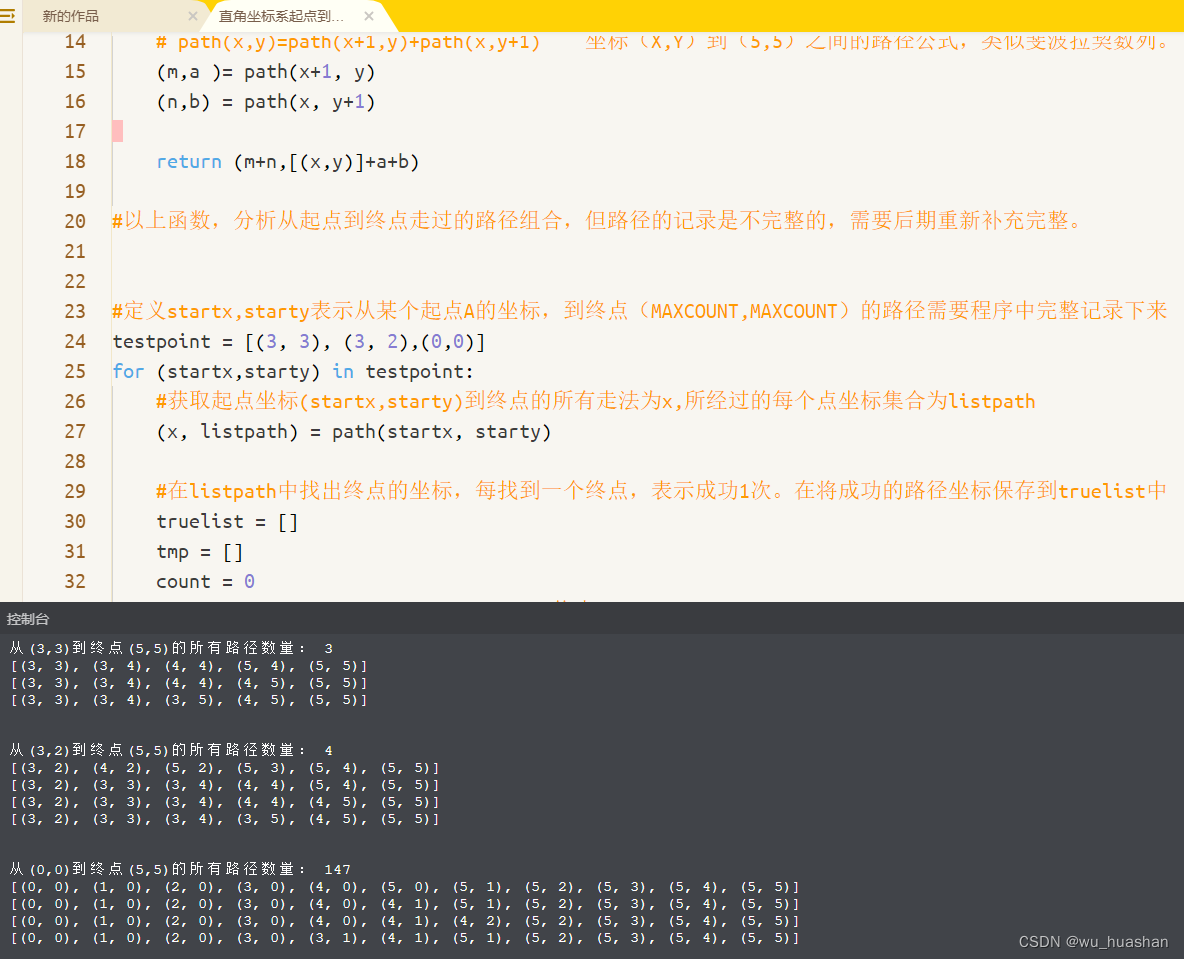
问题：在坐标系中第一象限内的点P（x,y）     x<6，y<6.  到终点（5,5）有多少种走法？并显示出现所经过的点坐标

限制条件：从起点坐标只能向上或者向右走。其中（4,3）是被断开的点。

MAXCOUNT =5 # 设置坐标系中出口的坐标位置M(5,5),计算A(x,y)到M点有多少种走法，要求只能向上或者向右走。

#path函数计算每个坐标点到终点的走法数量,并保存每个坐标到终点的所有经过点的坐标。
def path(x, y):
   
    # 初始化断点，如第四行第三列被阻断 path(4,3)=0，如阻断多个点，则增加若干if语句并返回(0,[])
    if x == 4 and y == 3:
        return (0,[])
    if x == MAXCOUNT and y == MAXCOUNT:  # 默认第5行第5列为出口，通，标记为1,path(5,5)=1
        return (1,[(x,y)])
    if x > MAXCOUNT or y > MAXCOUNT:  # 坐标(x,y)超过了5，则表示不通，标记为0,path(x,y)=0
        return (0,[])
  
    # path(x,y)=path(x+1,y)+path(x,y+1)    坐标（X,Y）到（5,5）之间的路径公式，类似斐波拉契数列。
    (m,a )= path(x+1, y)
    (n,b) = path(x, y+1)
 
    return (m+n,[(x,y)]+a+b)

#以上函数，分析从起点到终点走过的路径组合，但路径的记录是不完整的，需要后期重新补充完整。

#定义startx,starty表示从某个起点A的坐标，到终点（MAXCOUNT,MAXCOUNT）的路径需要程序中完整记录下来
testpoint = [(3, 3), (3, 2),(0,0)]
for (startx,starty) in testpoint:
    #获取起点坐标(startx,starty)到终点的所有走法为x,所经过的每个点坐标集合为listpath
    (x, listpath) = path(startx, starty)

    #在listpath中找出终点的坐标，每找到一个终点，表示成功1次。在将成功的路径坐标保存到truelist中
    truelist = []
    tmp = []
    count = 0
    OVERPOINT = (MAXCOUNT, MAXCOUNT)  # 终点
    #将listpath ----->truelist(以终点为目标得到truelist)
    for m in listpath:
        tmp.append(m)
        if m == OVERPOINT:
            truelist.append(tmp)
            count = count+1
            tmp = []
    print('从(%d,%d)到终点(%d,%d)的所有路径数量：' %
          (startx, starty, MAXCOUNT, MAXCOUNT), x)
   
    #print('-----路径列表------------------')
    if (len(truelist)>0):
        pre=len(truelist[0])
        print(truelist[0])
        for m in range(1,len(truelist)):
            current=len(truelist[m])
            addtemp=[]
            for n in range(0,pre-current):
                addtemp.append(truelist[m-1][n])
            truelist[m]=addtemp+truelist[m]
            pre=len(truelist[m])
            print(truelist[m])
    print('\n')