1、作者介绍

任正福，男，西安工程大学电子信息学院，2022级研究生
研究方向：混响背景下目标回波检测
电子邮件：1214061716@qq.com

陈梦丹，女，西安工程大学电子信息学院，2022级硕士研究生，张宏伟人工智能课题组
研究方向：机器视觉与人工智能
电子邮件：1169738496@qq.com

2、决策树算法

2.1 决策树原理

2.1.1 基本原理

决策树（Decision Tree）是一种非参数的有监督学习方法，它能够从一系列有特征和标签的数据中总结出决策规则，并用树状图的结构来呈现这些规则，以解决分类和回归问题。决策树算法容易理解，适用各种数据，在解决各种问题时都有良好表现，尤其是以树模型为核心的各种集成算法，在各个行业和领域都有广泛的应用。

比如说，来看看下面这组数据集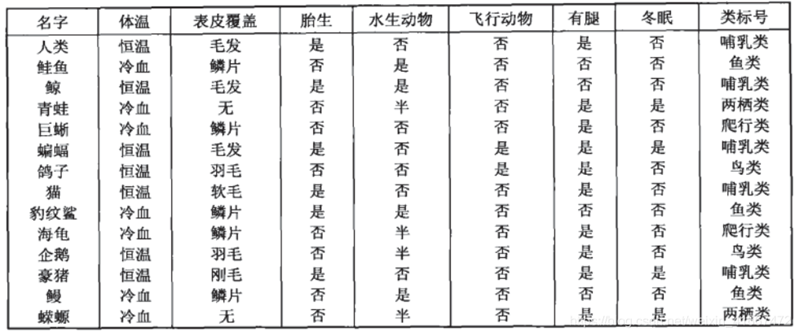：在这里插入图片描述
我们要做的是根据这些数据，来将动物分类，那么决策树是如何来完成这项工作的呢，它会给我们画一张图：

2.1.2 节点的概念

根节点：没有进边，有出边。包含最初的，针对特征的提问。
中间节点：既有进边也有出边，进边只有一条，出边可以有很多条。都是针对特征的提问。
叶子节点：有进边，没有出边，每个叶子节点都是一个类别标签。
子节点和父节点在两个相连的节点中，更接近根节点的是父节点，另一个是子节点。

决策树就是要在众多的属性中选取较重要的前几个属性来建立树。上图中的最初的问题所在的地方叫做根节点，在得到结论前的每一个问题都是中间节点，而得到的每一个结论（动物的类别）都叫做叶子节点。

那么决策树要解决的核心问题是什么呢？
（1）如何从数据表中找出最佳节点和最佳分枝？
（2）如何让决策树停止生长，防止过拟合？
几乎所有决策树有关的模型调整方法，都围绕这两个问题展开。

2.2 构建决策树

显然，任意一个数据集上的所有特征都可以被拿来分枝，特征上的任意节点又可以自由组合所以一个数据集上可以发展出非常非常多棵决策树，其数量可达指数级。在这些树中，肯定有一颗最好的，这个最好的树叫做"全局最优树"。

决策树构建的基本步骤如下：

开始，所有记录看作一个节点；
遍历每个变量的每一种分割方式，找到最好的分割点；
分割成两个节点N1和N2；
对N1和N2分别继续执行2-3步，直到每个节点足够“纯”为止。

如何评估分割点的好坏？如果一个分割点可以将当前的所有节点分为两类，使得每一类都很“纯”，也就是同一类的记录较多，那么就是一个好分割点。

2.3 决策树优缺点

决策树的优点：

易于理解和解释，因为树木可以画出来被看见。
需要很少的数据准备。其他很多算法通常都需要数据规范化，需要创建虚拟变量并删除空值等。但请注意， sklearn中的决策树模块不支持对缺失值的处理。
使用树的成本（比如说，在预测数据的时候）是用于训练树的数据点的数量的对数，相比于其他算法，这是一个很低的成本。
能够同时处理数字和分类数据，既可以做回归又可以做分类。其他技术通常专门用于分析仅具有一种变量类型的数据集。
能够处理多输出问题，即含有多个标签的问题，注意与一个标签中含有多种标签分类的问题区别开。

决策树的缺点：

决策树学习者可能创建过于复杂的树，这些树不能很好地推广数据。这称为过度拟合。修剪，设置叶节点所需的最小样本数或设置树的最大深度等机制是避免此问题所必需的，而这些参数的整合和调整对初学者来说会比较晦涩。
决策树可能不稳定，数据中微小的变化可能导致生成完全不同的树，这个问题需要通过集成算法来解决。
决策树的学习是基于贪婪算法，它靠优化局部最优（每个节点的最优）来试图达到整体的最优，但这种做法不能保证返回全局最优决策树。这个问题也可以由集成算法来解决，在随机森林中，特征和样本会在分枝过程中被随机采样。

3、实验设计

3.1 数据集简介

数据集下载：

泰坦尼克号数据集来源于kaggle官网，如果你已经注册过账号，可以直接在官网下载。

如果你没有注册或者注册失败（常见问题是没有验证码），你可以在国内的天池网站上下载。

数据集包含三个csv格式文件，train.csv为我们要使用的数据（既有特征又有标签，可以来训练和测试），test.csv为kaggle提供的测试集（无标签）
在这里插入图片描述
该数据集包含的变量：

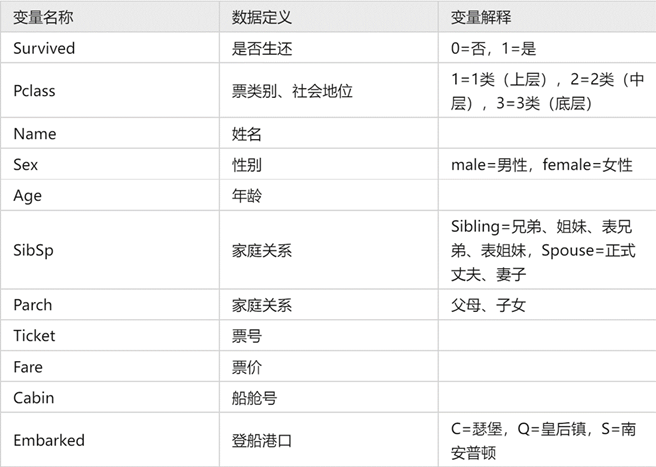
train.csv包含的具体信息：

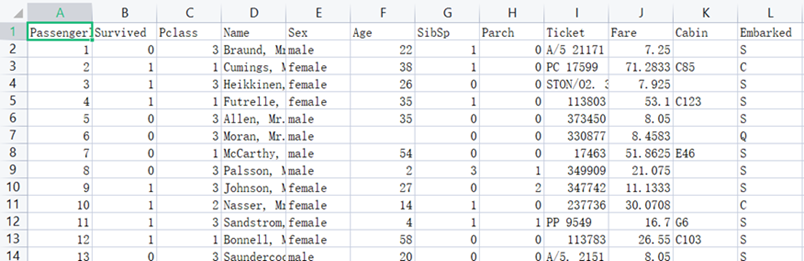
test.csv包含的具体信息：

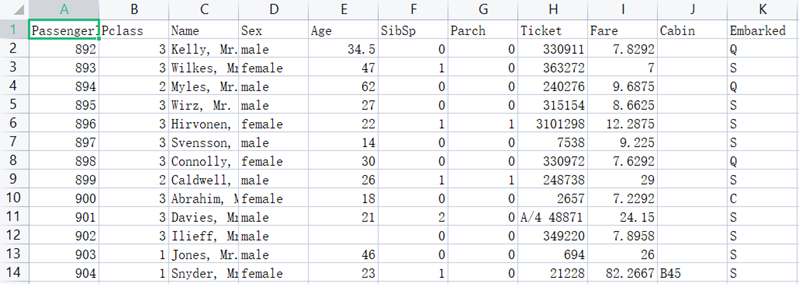
3.2 代码实现

完整代码：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import cross_val_score
from sklearn import tree
from sklearn.feature_extraction import DictVectorizer
from sklearn.tree import export_graphviz

data = pd.read_csv(r"train.csv")
data.info()

#删除冗余字段
data_new = data.drop(["Name","Ticket","Cabin"],axis=1)

#axis=1,轴向=1即对列进行操作
#使用年龄字段的均值填补缺失值
data_new["Age"] = data_new["Age"].fillna(data_new["Age"].mean())

#将embarked字段中含有缺失值的行删除
data_new.dropna(axis=0)
data_new.info()

#将sex、embarked字段转换为字段属性，可有两种不同的方法
labels = data_new["Embarked"].unique().tolist()
data_new["Embarked"] = data_new["Embarked"].apply(lambda x:labels.index(x))
data_new["Sex"] = (data_new["Sex"]=="male").astype("int")
#至此数据的基本处理已经结束
x = data_new.iloc[:,data_new.columns!="Survived"]
y = data_new.iloc[:,data_new.columns=="Survived"]
xtrain,xtest,ytrain,ytest = train_test_split(x,y,test_size=0.3)
for i in [xtrain,xtest,ytrain,ytest]:
    i.index = range(i.shape[0])

clf = DecisionTreeClassifier(random_state=25)
clf = clf.fit(xtrain,ytrain)
score = clf.score(xtest,ytest)
print('score：',score)

clf = DecisionTreeClassifier(random_state=25)
clf = clf.fit(xtrain,ytrain)
score_mean = cross_val_score(clf,x,y,cv=10).mean()
print('score_mean：',score)

#交叉验证的结果比单个的结果更低，因此要来调整参数，首先想到的是max_depth,因此绘制超参数曲线
score_test=[]
score_train=[]
for i in range(10):
    clf = DecisionTreeClassifier(random_state=25
                                ,max_depth=i+1)
    clf = clf.fit(xtrain,ytrain)
    score_tr = clf.score(xtrain,ytrain)
    score_te = cross_val_score(clf,x,y,cv=10).mean()
    score_train.append(score_tr)
    score_test.append(score_te)
print("\nbefore:",max(score_test))
#绘制超参数图像
plt.plot(range(1,11),score_train,color="red",label="train")
plt.plot(range(1,11),score_test,color="blue",label="test")
plt.legend()
plt.xticks(range(1,11))
plt.show()

#调整参数criterion，观察图像变化
score_test =[]
score_train = []
for i in range(10):
    clf = DecisionTreeClassifier(random_state=25
                                ,max_depth=i+1
                                ,criterion="entropy")
    clf = clf.fit(xtrain,ytrain)
    score_tr = clf.score(xtrain,ytrain)
    score_te = cross_val_score(clf,x,y,cv=10).mean()
    score_train.append(score_tr)
    score_test.append(score_te)
print("after:",max(score_test))
 #绘制图像
plt.plot(range(1,11),score_train,color="red",label="train")
plt.plot(range(1,11),score_test,color="blue",label="test")
plt.xticks(range(1,11))
plt.legend()
plt.show()

#parameters:本质是一串参数和这串参数对应的，我们希望网格搜索来搜索的参数的取值范围
parameters = {
    "splitter":("best","random")
    ,"min_samples_leaf":[*range(1,20,5)]
    ,"min_impurity_decrease":[*np.linspace(0,0.5,20)]
}
clf = DecisionTreeClassifier(random_state=25
                            ,max_depth=3
                            ,criterion="entropy")
clf.fit(xtrain,ytrain)
GS = GridSearchCV(clf,parameters,cv=10)
GS = GS.fit(xtrain,ytrain)
print('准确率：',GS.best_score_)
print(GS.best_params_)

3.3 运行结果

绘制超参数曲线，根据函数图像可以看到，当max_depth>3之后，训练集上的得分远远高于测试集上的得分，存在过拟合的现象，因此max_depth=3为较为合适的取值。
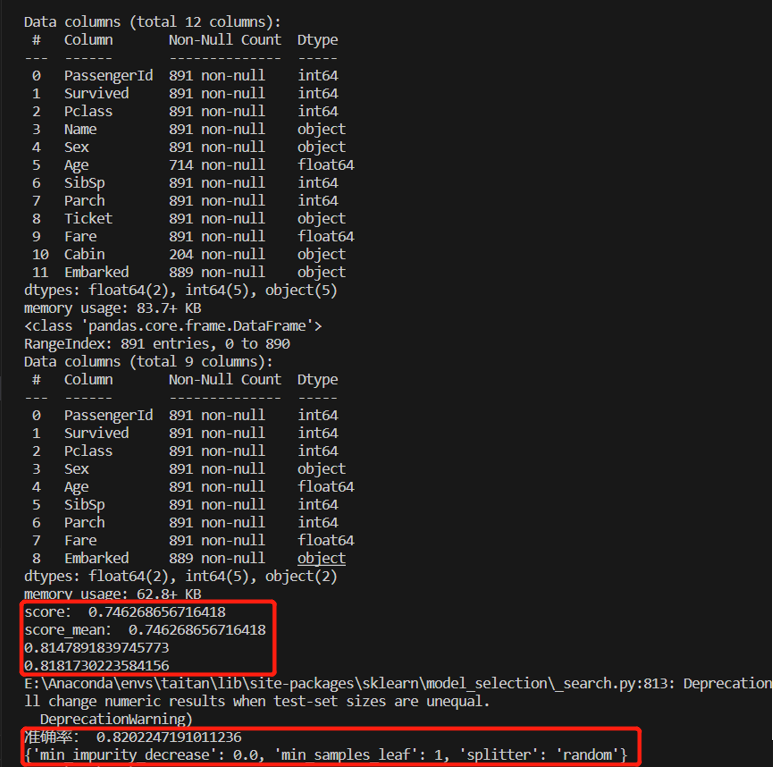
在这里插入图片描述调节参数之后，由图像观察可知，criterion="entropy"使得max_depth=3时两点更加接近，并且得分有所提高，如下图的0.8181730