Tag：贪心；动态规划

题目

1. N块石头排成一行，每块石头有各自固定的位置。两个玩家依次取石头，每个玩家每次可以取其中任意一块石头，或者相邻的两块石头，石头在游戏过程中不能移位（即编号不会改变），最后能将剩下的石头一次取光的玩家获胜。这个游戏有必胜策略嘛？
2. 有N块石头和两个玩家A和B，玩家A先将石头分成若干堆，然后按照BABA的顺序不断轮流取石头，能将剩下的石头一次取光的玩家获胜。每次取石头时，每个玩家只能从若干堆石头中任选一堆，取这一堆石头中任意数目（大于0）个石头。玩家A怎么分配和取石头才能保证自己获胜？
3. 假设有两堆石头，有两个玩家会根据如下的规则轮流取石头：
   1. 每人每次可以从两堆石头中各取出数量相等的石头，或者仅从一堆石头中取出任意数量的石头；
   2. 最后把剩下的石头一次拿光的人获胜。

思路与算法

问题一

假设编号为1,2,3,4,5.取相邻的两块石头是指可以取12，但是如果先把2号石头拿走了，是不可以取13的，认定此时两块石头是不相邻的。
我们可以先用列举的方式来找规律，假设A先取：
N = 1，A必赢；
N = 2，A必赢；
N = 3，A取中间的必赢；
N = 4，A取中间的两个必赢；
N = 5，A取中间的一个必赢；
N = 6，A先取中间的两个必赢；
…
A取中间的石头使得左右两边留下相同的数目就必赢（如果N为偶数，取中间的两个；如果N为奇数，取中间的一个）。

思考：如果最后能将剩下的石头一次取光的玩家判定为输，那是否有必胜策略呢？

同样先来列举思路，假设A先取：
N = 1，<1>，A必输；
N = 2，<1,1>，A只拿一个必赢；
N = 3，<1,1,1>，A只拿相邻两个,剩下<1>,必赢；
N = 4，<1,1,1,1>，A拿走最边上的一块变成<1,1,1>;拿走最边上的两块变成<1,1>;拿走中间的一块变成<1,1,0,1>;拿走中间的两块变成<1,0,0,1>；都必输；
N = 5，<1,1,1,1,1>，A拿走最边上的一块变成<1,1,1,1>必赢；
…

对于N块石头,N足够大.便有以下结论:
如果N块石头你必输的话,那么N+1,N+2你必赢.因为你可以取走边角的1块或2块,然后就剩下了N块石头,并且是对手取,对手必然会输.
所以推出（k为任意整数）：
N = 3K + 1.B赢
N = 3K + 2,A赢
N = 3K + 3,A赢

问题二

同样用列举的方式，用N表示石头的堆数，M表示总的石头数目。
当N = 1 时，A必输；
N = 2，如果（1,1）A必赢；如果（1，X），B可以拿走小于X - 1 的石头，A必输；如果（2,2）（3,3）…都是A必赢；
…
当摆放方法为（1,1，…，1）的时候，如果1的个数是奇数个，则先拿者赢；如果1的个数是偶数个，则先拿者必输；
当摆放方法为（1,1，…,1,X)，先拿者必赢；
此外还有其他的摆放方法，比如N = 9，（2,3,4）
可以考虑异或原理：
XOR（0,0） = 0
XOR（1,0） = 1
XOR（1,1） = 1
推理整个游戏过程，从N堆石头（M1，M2，M3）开始，石头一直递减到全部为（0,0，…,0）
当M为奇数时，无论怎么分堆，都是B赢；其他的我们只要保证每次将XOR（M1，M2，…,M3) = 0,就能保证赢的局面。

问题三

可以利用质数筛子的方法来列举，用数对(m,n)表示一堆石头有m块，另一堆有n块。删除所有A必赢的局面：

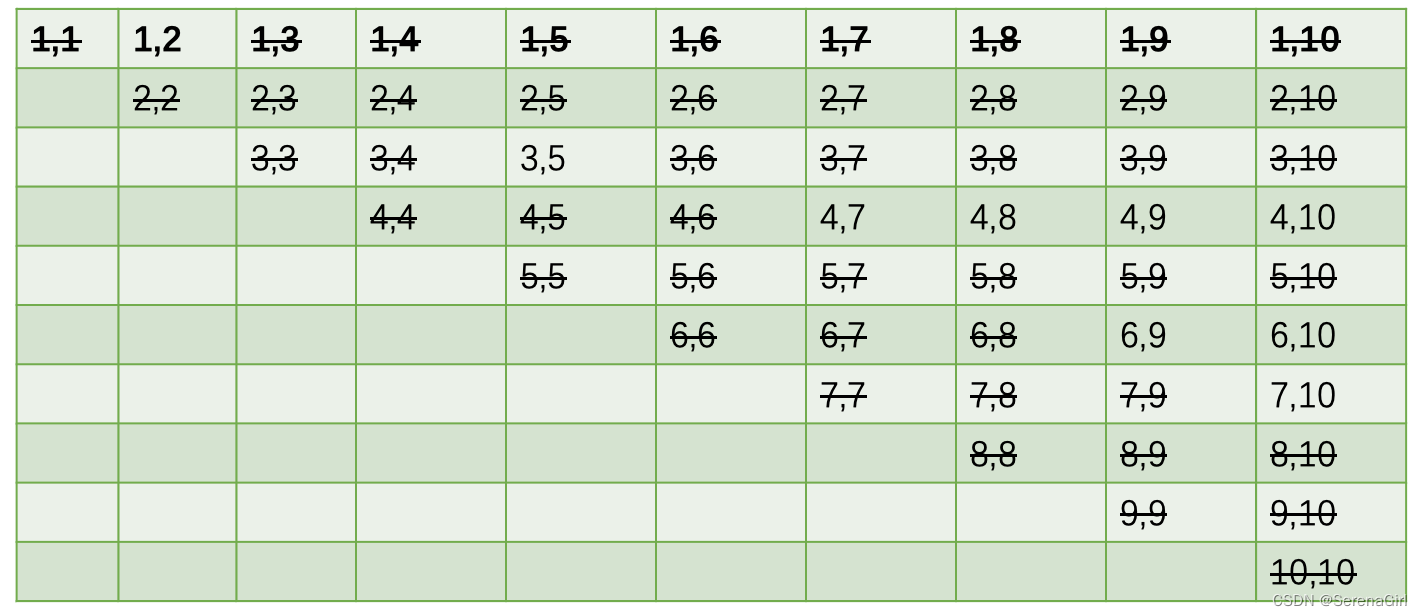
剩下的如下图：

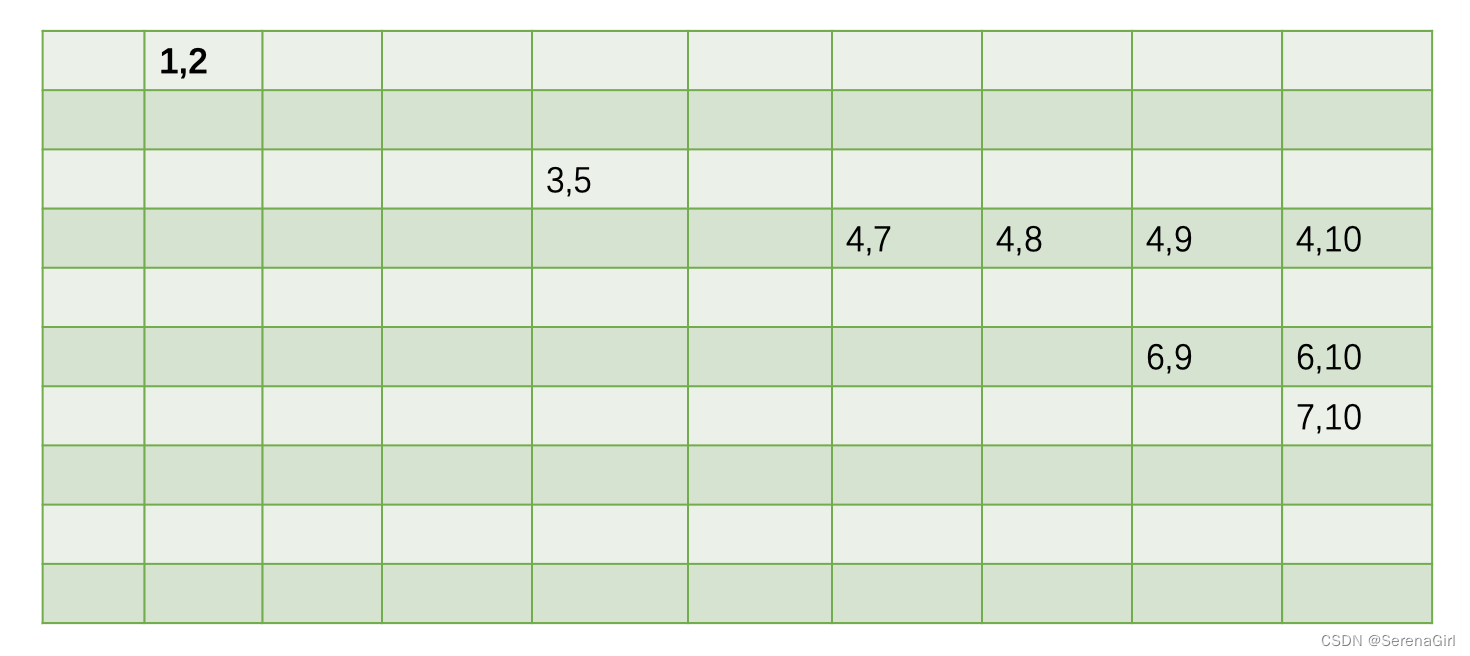
可以得出结论，一般而言，第n组的不安全局面(an,bn)可以由以下定义得到：

1. a1 = 1, a2 = 2;
2. 若a1,b1,…,an - 1,bn - 1已经求得，则定义an为未出现在这2n-2个数中的最小整数
3. bn = an + n;
   做成表格：
   
   两堆石子的个数只要不能由表格中的数据推出来，则说明A必胜。