[论文阅读] 颜色迁移-直方图渐进式颜色迁移

文章: 有2篇相关的文章, 都为同一作者

• [Progressive histogram reshaping for creative color transfer and tone reproduction], [code未公开]
• [Progressive color transfer for images of arbitrary dynamic range], [code未公开]

其它相关资料:

• Tania Pouli, 作者主页
• [paper] Progressive Histogram Reshaping for Creative Color Transfer and Tone Reproduction | 逍遥文工作室 (cg2010studio.com)

1-算法原理

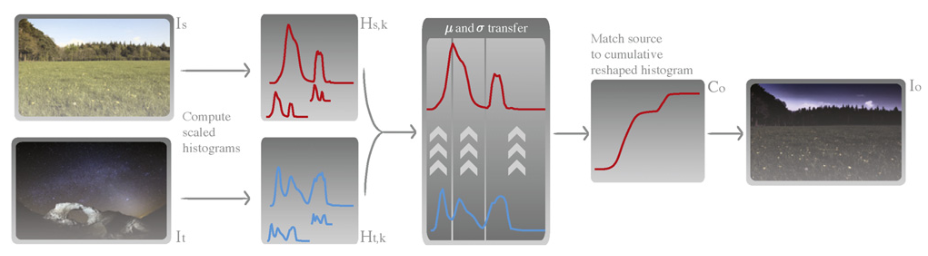
本文算法核心还是直方图匹配, 但本文的新颖性主要体现在不同尺度的直方图渐进式局部重塑, 如下图所示:

1.1-不同尺度

首先来说下不同尺度, 通过如下所示来统计直方图, 不同的V即为不同的尺度.

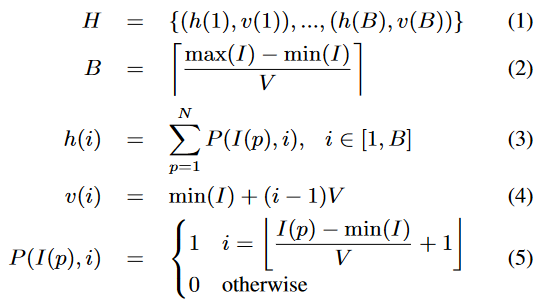
如上图中, 不同长度的直方图即为不同V的直方图.

1.2-局部重塑

直方图中的一个峰值对应一个分布, 也对应图像中某一个区域. 局部重塑就是对直方图的每个峰进行调整, 如下所示, [a,b]为一个局部区域范围:


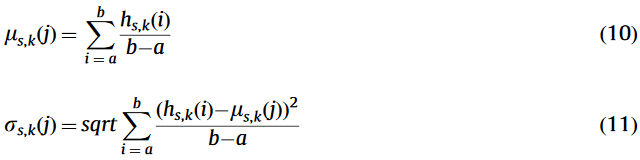
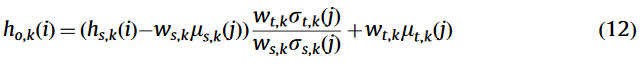
如上图中所示.

1.3-渐进

类似金字塔结构, 一个尺度的结果作为下一个尺度的初始值, 从而实现渐进式处理过程.

1.4-算法流程

如下所示为算法的整体流程:

本文算法是在Lab颜色空间进行的, 对每个颜色空间分别单独处理, 下面仅介绍一个颜色通道的处理方法:

1. 统计源图像$Is$和目标图像$It$的直方图 $Hs$, $Ht$
2. 使用下/上采样得到不同尺度的直方图, $Hs,k$ 和 $Ht,k$
3. 查找目标图像直方图$Ht,k$的峰值, 找到局部区域 $Rmin,t$, 每个区域为 $[a=R_{min,k}(j),b=R_{min,k}(j+1)-1]$
4. 使用上述公式(10)-(12)对直方图 $Hs,k$ 进行局部重塑, 得到 $Hs,k^{\prime }$
5. 查找处理后的直方图 $Hs,k^{\prime }$ 的直方图峰值, 找到局部区域 $Rmin,s$
6. 使用上述公式(10)-(12)对直方图 $Hs,k^{\prime }$ 进行局部重塑, 得到当前尺度的直方图输出 $Ho$, 并将其作为下一个尺度的输入 $Hs$
7. 所有尺度处理完后, 得到最终的直方图输出$Ho$
8. 对当前颜色通道进行直方图匹配, $Ho$为待匹配直方图

2-算法核心

这里觉得算法的关键有2个地方: 一个是不同尺度的实现, 一个是渐进式局部重塑.

2.1-不同尺度实现

本文使用插值算法对最原始的直方图进行缩放从而实现不同的尺度, 而不是直接使用公式进行计算, 可能是以下几个原因:

1. 直接使用公式计算直方图时, 可能某些bin没有数据, 得到的直方图不连续, 不方便后续处理
2. 使用插值方法, 具有一定的平滑性, 这样得到直方图就比较平滑, 这样后续处理时不会出现太大的问题

文中使用双立方进行下采样, 最邻近方法进行上采样. 文中说插值方法对结果影响不大, 但这里有个问题, 就是上采样使用最近邻时, 对于某些尺度可能会出现很明显的锯齿现象.

2.2-渐进式局部重塑

如下图所示为渐进式重塑的一个示例

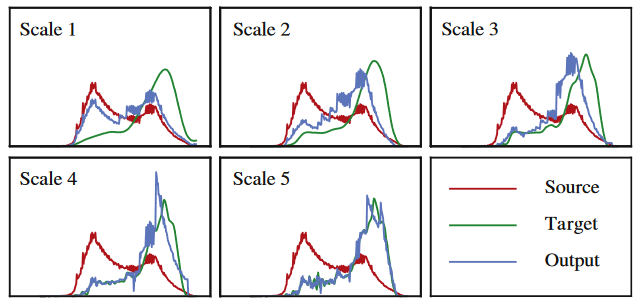
局部重塑是通过公式(10)-(12)实现的, 这里补充说明下:

• 这里重塑的仅是直方图中bin的统计值, 即这个bin中像素的个数, 而不是bin的值(对应的灰度值)
• 如果不同局部区域的缩放和平移不同, 就会在相邻的区域上出现阶跃跳变, 如上图所示的蓝色线条output

尺度的个数$S_{max}$是通过如下公式进行计算的:

$$S_{max}=\lfloor lo{g}_2(\frac{B}{B_{min}})\rfloor \text{\hspace{1em}(7)}$$

每个尺度里面中直方图bin的个数为 $B_k=B\ast 2^{k-S_{max}}$:

• k=1时, 直方图bin的个数$B_k$最小, 这样的尺度最大最粗, 这样源图像直方图的高频内容就会被保留, 低频则从目标图像转移得到, 实现颜色迁移
• k=$S_{max}$时, 直方图bin的个数$B_k$最大, 这样的尺度最小最精细, 这样就类似与直接使用直方图匹配

通过设置尺度个数$k=ratio\ast S_{max}$就可以实现不用比例的重塑, 从而实现不同程度的颜色迁移控制, 如下所示:

3-算法效果

如下所示都为HDR图像结果:

HDR和LDR结果:

4-补充说明

文中对上述算法存在的问题进行了说明并提出了解决方法.

4.1-局部伪影问题

由于以下几个方面的原因, 可能导致最后的结果会出选局部伪影:

• 图像质量过低, 或者压缩过度, 压缩造成的马赛克效应会被放大
• 图像平滑区域会出现颜色渐变, 这种渐变色被处理后可能会不平滑

作者给出的解决方法是, 使用双边滤波进行局部细节处理:


如下所示为处理后结果对比:

4.2-区域选择

有时候需要额外的控制来指定源图像(目标图像)哪些区域需要进行颜色迁移, 哪些区域不需要进行颜色迁移, 这是由于这些区域可能存在不正常的颜色迁移. 如下图所示的白虎变成了红色.

这些区域都属于消色(黑白灰三种颜色)区域, 本文提出了一种检测这种区域的方法, 在Lab颜色空间的a,b通道使用如下公式进行计算得到:

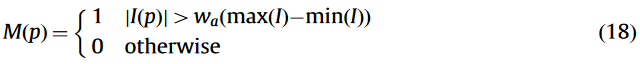
上图中d图为后处理后的图像, 白虎的颜色正常. 但文中对于怎么使用这个区域说的不够详细, 看的不是很明白.

5-算法复现

使用matlab复现结果如下所示:

依次为源图像, 目标/参考图像, 结果