本文目录
- 0 引言
- 1 度量差异性
- 1.1 闵可夫斯基距离(Minkowski distance)
- 1.1.1 欧氏距离(Euclidean distance)
- 1.1.2 曼哈顿距离(Manhattan distance)
- 1.1.3 切比雪夫距离(Chebyshev distance)
- 1.2 熵
- 1.2.1 信息熵
- 1.2.2 相对熵(KL散度)
- 1.2.3 交叉熵
- 1.3 汉明距离
- 1.4 杰卡德距离(Jaccard Distance)
- 2 度量相似性
- 2.1 夹角余弦(余弦相似度)
- 2.2 杰卡德相似系数(Jaccard similarity coefficient)
- 2.3 协方差
- 2.4 Pearson相关系数
- 2.5 Spearman相关系数
- 2.6 Kendall相关系数
- 3 度量分布
- 3.1 直方图(Histogram)
- 3.2 偏度(skewness)
- 3.3 峰度(Kurtosis)
- 3.4 雅克-贝拉检验(Jarque-Bera)
- 4 度量位置
- 4.1 直方图的向量
- 4.2 Embedding方法
- 参考资料
0 引言
不管是机器学习还是运筹优化方向,数学建模中的一个重要任务就是量化。不同任务中对分析对象的度量方法也是多样的,建模者可以恰当地选取常用的度量方法,也可以针对性地设计特殊的度量方法。本文总结工作学习中接触到的常用度量方法,熟悉这些方法和适用场景对于大家数学建模工作及启发设计新的度量方法是非常帮助的。内容会不定期持续更新,建议先收藏+关注。
世界上一起抽象和具体事物都可以视为对象。按照面向对象的思想,度量方法就基本分为:
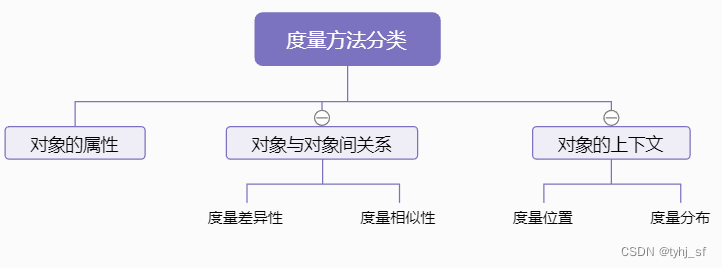
注意:
- 对象属性如大小、颜色、亮度、甜度等等一系列,还有些特殊定义的,种类繁多,不在本文考虑之列;
- 差异性与相似性是相反的关系;
- 位置信息是相对整体的,即与上下文(context)密切相关。
1 度量差异性
1.1 闵可夫斯基距离(Minkowski distance)
闵可夫斯基距离 (Minkowski Distance),也被称为 闵氏距离。它不仅仅是一种距离,而是将多个距离公式(曼哈顿距离、欧式距离、切比雪夫距离)总结成为的一个公式。
n维空间上两点A、B,其中A向量为
(
a
1
,
a
2
.
.
.
a
n
)
(a_1,a_2...a_n)
(a1,a2...an),B向量为
(
b
1
,
b
2
.
.
.
b
n
)
(b_1,b_2...b_n)
(b1,b2...bn),A、B向量之间的闵可夫斯基距离公式:
d
A
B
=
(
∑
i
=
1
n
∣
a
i
−
b
i
∣
p
)
1
p
d_{AB} = ({\sum_{i=1}^{n}{|a_i - b_i|^p}})^{\frac{1}{p}}
dAB=(i=1∑n∣ai−bi∣p)p1
其中,
p
p
p为任意正整数。
该公式也是
a
i
−
b
i
a_i - b_i
ai−bi的
L
p
L_p
Lp范数
∣
∣
a
i
−
b
i
∣
∣
p
||a_i - b_i||_p
∣∣ai−bi∣∣p
用途
机器学习中常用
L
1
,
L
2
L_1, L_2
L1,L2范数。
缺点:
- 向量的各个维度的取值可能在不同量纲(scale)下(比如身高和体重),维度之间的值运算可能没有意义。
- 未考虑各个分量的分布(期望,方差等)可能是不同的。有的维度值整体比较大,有的维度值整体比较小。因此各个维度平方差值直接求和会使 d A B d_{AB} dAB对取值较大的维度更敏感。因此,可以对各个维度先进行规范化(也称标准化)处理,比如最小最大规范化、z-score标准化、小数定标规范化等等,这里不细讲。
1.1.1 欧氏距离(Euclidean distance)
欧氏距离是
p
=
2
p=2
p=2的闵可夫斯基距离。
n维空间上两点A、B,其中A向量为
(
a
1
,
a
2
.
.
.
a
n
)
(a_1,a_2...a_n)
(a1,a2...an),B向量为
(
b
1
,
b
2
.
.
.
b
n
)
(b_1,b_2...b_n)
(b1,b2...bn),A、B向量之间的欧式距离公式:
d
A
B
=
(
∑
i
=
1
n
∣
a
i
−
b
i
∣
2
)
1
2
=
(
∑
i
=
1
n
(
a
i
−
b
i
)
2
)
1
2
\begin {alignedat}{2} d_{AB} &= ({\sum_{i=1}^{n}{|a_i - b_i|^2}})^{\frac{1}{2}} \\ &=({\sum_{i=1}^{n}{(a_i - b_i)^2}})^{\frac{1}{2}} \end {alignedat}
dAB=(i=1∑n∣ai−bi∣2)21=(i=1∑n(ai−bi)2)21
1.1.2 曼哈顿距离(Manhattan distance)
曼哈顿距离是
p
=
1
p=1
p=1的闵可夫斯基距离,也称“街区距离”(city block distance)。
n维空间上两点A、B,其中A向量为
(
a
1
,
a
2
.
.
.
a
n
)
(a_1,a_2...a_n)
(a1,a2...an),B向量为
(
b
1
,
b
2
.
.
.
b
n
)
(b_1,b_2...b_n)
(b1,b2...bn),A、B向量之间的曼哈顿距离公式:
d
A
B
=
∑
i
=
1
n
∣
a
i
−
b
i
∣
d_{AB} = \sum_{i=1}^{n}{|a_i - b_i|}
dAB=i=1∑n∣ai−bi∣
1.1.3 切比雪夫距离(Chebyshev distance)
切比雪夫距离是
p
→
∞
p\to \infty
p→∞时的闵可夫斯基距离。
n维空间上两点A、B,其中A向量为
(
a
1
,
a
2
.
.
.
a
n
)
(a_1,a_2...a_n)
(a1,a2...an),B向量为
(
b
1
,
b
2
.
.
.
b
n
)
(b_1,b_2...b_n)
(b1,b2...bn),A、B向量之间的切比雪夫距离公式:
d
A
B
=
lim
p
→
∞
(
∑
i
=
1
n
∣
a
i
−
b
i
∣
p
)
1
p
=
max
i
=
1
n
∣
a
i
−
b
i
∣
\begin {alignedat}{2} d_{AB} &= \lim\limits_{p\to \infty} ({\sum_{i=1}^{n}{|a_i - b_i|^p}})^{\frac{1}{p}} \\ &=\max_{i=1}^{n} |a_i - b_i| \end {alignedat}
dAB=p→∞lim(i=1∑n∣ai−bi∣p)p1=i=1maxn∣ai−bi∣
1.2 熵
1.2.1 信息熵
1948 年,伟大的信息论之父香农(Shannon)将热力学中熵的概念引入到了信息论中,提出了信息熵这一概念。这里的“信息”指来自总体分布或数据流中的事件、样本或特征。
信息熵用于度量信息的不确定性程度,将原本模糊的信息概念进行计算得出精确可比较的值。信息熵值越大,信息的不确定性越大。
给定事件集合X, 其中某一事件 x i x_i xi发生的概率为 P ( x i ) P(x_i) P(xi), 事件 x i x_i xi的不确定性的值 f ( x i ) f(x_i) f(xi)需要满足:
- 不确定性值 f ( x i ) f(x_i) f(xi)与事件 x i x_i xi的概率 P ( x i ) P(x_i) P(xi)成反比,即事件概率越大,不确定性就越小,当事件概率为1时,不确定性为0;
- 两个独立事件所产生的不确定性应等于各自不确定性之和,即 f ( x i , x j ) = f ( x i ) + f ( x j ) f(x_i,x_j)=f(x_i)+f(x_j) f(xi,xj)=f(xi)+f(xj)。
因此定义不确定性值
f
(
x
i
)
f(x_i)
f(xi)为:
f
(
x
i
)
=
−
l
o
g
P
(
x
i
)
f(x_i) = -log\ P(x_i)
f(xi)=−log P(xi)
事件集合X包含的信息不确定性为所有事件的各自确定性之和,即信息熵,形式化表示为H(X):
H
(
X
)
=
E
[
f
(
x
i
)
]
=
−
∑
i
n
P
(
x
i
)
l
o
g
P
(
x
i
)
\begin {alignedat}{2} H(X)&=E[f(x_i)] \\ &=-\sum_i^n P(x_i) log\ P(x_i) \end {alignedat}
H(X)=E[f(xi)]=−i∑nP(xi)log P(xi)
1.2.2 相对熵(KL散度)
相对熵又称Kullback-Leibler散度(简称KL散度),如果我们对于同一个随机变量 X 有两个单独的概率分布 P(X) 和 Q(X),我们可以使用 KL 散度来度量这两个分布的差异性。
KL散度定义为两个概率分布的信息熵的差值,其计算公式:
D
K
L
(
P
(
X
)
∣
∣
Q
(
X
)
)
=
∑
i
=
1
n
P
(
x
i
)
l
o
g
(
P
(
x
i
)
Q
(
x
i
)
)
\begin {alignedat}{2} D_{KL}(P(X)||Q(X)) = \sum_{i=1}^nP(x_i)log(\frac{P(x_i)}{Q(x_i)}) \end {alignedat}
DKL(P(X)∣∣Q(X))=i=1∑nP(xi)log(Q(xi)P(xi))
其中,n为所有事件的个数。
D
K
L
D_{KL}
DKL的值越小,表示Q(X)分布和P(X)分布越接近。
应用:
在机器学习分类任务中(假设分为三类),P往往用来表示样本的真实分布,比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布,比如[0.7,0.2,0.1] 。
1.2.3 交叉熵
根据前面KL散度的公式我们可以继续推导出如下过程:
D
K
L
(
P
(
X
)
∣
∣
Q
(
X
)
)
=
∑
i
=
1
n
P
(
x
i
)
l
o
g
(
P
(
x
i
)
)
−
∑
i
=
1
n
P
(
x
i
)
l
o
g
(
Q
(
x
i
)
)
=
−
H
(
P
(
X
)
)
+
[
−
∑
i
=
1
n
P
(
x
i
)
l
o
g
(
Q
(
x
i
)
)
]
=
−
H
(
P
(
X
)
)
+
H
(
P
(
X
)
,
Q
(
X
)
)
\begin {alignedat}{2} D_{KL}(P(X)||Q(X)) &=∑_{i=1}^{n}P(x_i)log(P(x_i))−∑_{i=1}^{n}P(x_i)log(Q(x_i)) \\ &=-H(P(X))+[−∑_{i=1}^{n}P(x_i)log(Q(x_i))] \\ &=-H(P(X))+H(P(X),Q(X)) \end {alignedat}
DKL(P(X)∣∣Q(X))=i=1∑nP(xi)log(P(xi))−i=1∑nP(xi)log(Q(xi))=−H(P(X))+[−i=1∑nP(xi)log(Q(xi))]=−H(P(X))+H(P(X),Q(X))
其中,
H
(
P
(
X
)
)
H(P(X))
H(P(X))恰巧就是P(X)的熵:
H
(
P
(
X
)
)
=
−
∑
i
=
1
n
P
(
x
i
)
l
o
g
(
P
(
x
i
)
)
\begin {alignedat}{2} H(P(X))=-∑_{i=1}^{n}P(x_i)log(P(x_i)) \end {alignedat}
H(P(X))=−i=1∑nP(xi)log(P(xi))
$H(P(X),Q(X)) $就是交叉熵
H
(
P
(
X
)
,
Q
(
X
)
)
=
−
∑
i
=
1
n
P
(
x
i
)
l
o
g
(
Q
(
x
i
)
)
\begin {alignedat}{2} H(P(X),Q(X)) = −∑_{i=1}^{n}P(x_i)log(Q(x_i)) \end {alignedat}
H(P(X),Q(X))=−i=1∑nP(xi)log(Q(xi))
应用:
一般在机器学习中直接用交叉熵做loss评估模型,其中
P
(
x
i
)
P(x_i)
P(xi)是训练样本的label真实概率值,
Q
(
x
i
)
Q(x_i)
Q(xi)是对训练样本predict的概率值。由于KL散度中的前一部分
−
H
(
P
(
X
)
)
-H(P(X))
−H(P(X))的值在模型训练时是保持不变的(因为样本的标签不变),故在优化过程中,只需要关注交叉熵就可以了,也避免了不必要的计算。
1.3 汉明距离
两个等长的有序集合对应位置的不同元素的个数。
例如
- 1011101 1011101 1011101与 1001001 1001001 1001001 之间的汉明距离是2;
- 2143896 2143896 2143896与 2233796 2233796 2233796之间的汉明距离是3;
- 有序集合 { 1 , 3 , 2 a , 10 , k k } \{1, 3, 2a, 10, kk\} {1,3,2a,10,kk}与 有序集合 { 1 , 99 , 2 a , 10 , m m m } \{1, 99, 2a, 10, mmm\} {1,99,2a,10,mmm}之间的汉明距离是 2;
1.4 杰卡德距离(Jaccard Distance)
它是杰卡德相似系数的补集,被定义为1减去Jaccard相似系数。
给定集合A, B,则两集合的杰卡德相似系数J(A, B)为:
d
A
B
=
1
−
J
(
A
,
B
)
=
1
−
∣
A
∩
B
∣
∣
A
∪
B
∣
\begin {alignedat}{2} d_{AB} &= 1 - J(A,B) \\ &=1 - \frac{|A \cap B|}{|A \cup B|} \end {alignedat}
dAB=1−J(A,B)=1−∣A∪B∣∣A∩B∣
用途
度量两个集合(序列、向量等)之间的差异性。
2 度量相似性
2.1 夹角余弦(余弦相似度)
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近1,就表明夹角越接近0度,也就是两个向量越相似。
n维空间上两点A、B,其中A向量为
(
a
1
,
a
2
.
.
.
a
n
)
(a_1,a_2...a_n)
(a1,a2...an),B向量为
(
b
1
,
b
2
.
.
.
b
n
)
(b_1,b_2...b_n)
(b1,b2...bn),A、B向量之间的夹角余弦公式:
s
A
B
=
A
B
∣
∣
A
∣
∣
2
⋅
∣
∣
B
∣
∣
2
=
∑
i
=
1
n
a
i
b
i
∑
i
=
1
n
b
i
2
∑
i
=
1
n
a
i
2
\begin {alignedat}{2} s_{AB} &= \frac{AB}{||A||_2 \cdot ||B||_2}\\ &= \frac {\sum_{i=1}^{n} {a_i b_i}}{\sqrt{\sum_{i=1}^n b_i^2} \sqrt{\sum_{i=1}^n a_i^2}} \end {alignedat}
sAB=∣∣A∣∣2⋅∣∣B∣∣2AB=∑i=1nbi2∑i=1nai2∑i=1naibi
2.2 杰卡德相似系数(Jaccard similarity coefficient)
它被定义为两个集合交集的元素个数除以并集的元素个数。
给定集合A, B,则两集合的杰卡德相似系数J(A, B)为:
J
(
A
,
B
)
=
∣
A
∩
B
∣
∣
A
∪
B
∣
J(A,B)=\frac{|A \cap B|}{|A \cup B|}
J(A,B)=∣A∪B∣∣A∩B∣
用途
度量两个集合(序列、向量等)之间的相似性。
2.3 协方差
用来度量两个随机变量之间的独立性,这也是相似性的一种。协方差表示的是两个变量总体误差的期望。
给定两个随机变量X, Y,则协方差Cov(X,Y):
C
o
v
(
X
,
Y
)
=
E
[
(
X
−
E
[
X
]
)
−
(
Y
−
E
[
Y
]
)
]
=
E
[
X
Y
]
−
E
[
X
]
E
[
Y
]
\begin {alignedat}{2} Cov(X,Y) &= E[(X-E[X]) - (Y-E[Y])] \\ &=E[XY] - E[X]E[Y] \end {alignedat}
Cov(X,Y)=E[(X−E[X])−(Y−E[Y])]=E[XY]−E[X]E[Y]
协方差=0:两个随机变量称为是不相关的;
协方差>0:两个随机变量X, Y的变化趋势一致,也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值;
协方差<0:两个随机变量X, Y的化趋势相反,即其中一个变量大于自身的期望值时另外一个却小于自身的期望值;
缺点:
只能用于随机变量X, Y的量纲相同,整体取值范围比较接近的情况。否则使用之前需要进行规范化处理。
2.4 Pearson相关系数
Pearson相关系数度量两个连续变量的线性相似性。
给定两个变量X, Y,每个变量的样本集的元素个数均为n,协方差为Cov(X,Y), 方差分别为D(X),D(Y),则Pearson相关系数
ρ
(
X
,
Y
)
\rho(X,Y)
ρ(X,Y)定义为:
ρ
(
X
,
Y
)
=
C
o
v
(
X
,
Y
)
D
(
X
)
D
(
Y
)
=
∑
n
X
Y
−
∑
n
X
∑
n
Y
n
∑
n
X
2
−
(
∑
n
X
)
2
n
∑
n
Y
2
−
(
∑
n
Y
)
2
n
\begin {alignedat}{2} \rho(X,Y) &= \frac {Cov(X,Y)}{D(X)D(Y)} \\ &=\frac{\sum^n XY - \frac{\sum^n X \sum^nY}{n}}{\sqrt{\sum^n X^2 - \frac{(\sum^n X)^2}{n}} \sqrt{\sum^n Y^2 - \frac{(\sum^n Y)^2}{n}}} \end {alignedat}
ρ(X,Y)=D(X)D(Y)Cov(X,Y)=∑nX2−n(∑nX)2∑nY2−n(∑nY)2∑nXY−n∑nX∑nY
取值范围为[-1, 1]。在显著性的前提下,绝对值越大,相关性越强。
ρ
(
X
,
Y
)
>
0
\rho (X,Y)>0
ρ(X,Y)>0:表示变量X, Y正相关;
ρ
(
X
,
Y
)
<
0
\rho (X,Y)<0
ρ(X,Y)<0:表示变量X, Y负相关;
ρ
(
X
,
Y
)
=
0
\rho (X,Y)=0
ρ(X,Y)=0:表示变量X, Y无线性关系(无法证明不相关);
∣
ρ
(
X
,
Y
)
∣
=
1
|\rho (X,Y)|=1
∣ρ(X,Y)∣=1:表示变量X, Y完全线性相关。
适用条件:
- 两个变量要分别服从正态分布,通常用t检验检查相关系数的显著性;
- 两个变量的标准差不能为0;
- 样本容量n要大于20.
2.5 Spearman相关系数
Spearman相关系数度量两个连续变量的线性相似性。
给定两个变量X, Y,每个变量的样本集的元素个数均为n, 则Spearman相关系数
ρ
(
X
,
Y
)
\rho (X,Y)
ρ(X,Y)定义为:
ρ
(
X
,
Y
)
=
1
−
6
∑
i
=
1
n
(
d
i
)
n
(
n
2
−
1
)
\rho (X,Y) = 1-\frac{6\sum_{i=1}^{n}(d_i)}{n(n^2 - 1)}
ρ(X,Y)=1−n(n2−1)6∑i=1n(di)
ρ
(
X
,
Y
)
\rho (X,Y)
ρ(X,Y)值与两个样本集的元素值无关,而仅仅与其值之间的大小关系有关,取值范围为[-1, 1]。
d
i
d_i
di表示两个样本集分别排序后同位置的元素之差。
在显著性的前提下,绝对值越大,相关性越强。
ρ
(
X
,
Y
)
>
0
\rho (X,Y)>0
ρ(X,Y)>0:表示变量X, Y正相关;
ρ
(
X
,
Y
)
<
0
\rho (X,Y)<0
ρ(X,Y)<0:表示变量X, Y负相关;
ρ
(
X
,
Y
)
=
0
\rho (X,Y)=0
ρ(X,Y)=0:表示变量X, Y无线性关系(无法证明不相关);
∣
ρ
(
X
,
Y
)
∣
=
1
|\rho (X,Y)|=1
∣ρ(X,Y)∣=1:表示变量X, Y完全线性相关。
适用条件:
- Spearman相关系数可以度量两个连续变量的非单调线性相似性,这比Pearson相关系数要好一些;
- 与变量的分布无关;
- 如果Pearson相关系数无法应用的数据集则可以试试Spearman相关系数。
- 样本集容量要大于20.
2.6 Kendall相关系数
Kendall相关系数度量两个有序离散型变量的相似性。
给定两个变量X, Y,每个变量的样本集的元素个数均为n, 则Kendall相关系数
ρ
(
X
,
Y
)
\rho (X,Y)
ρ(X,Y)为同序对(concordant pairs)和异序对(discordant pairs)之差与总对数(n*(n-1)/2)的比值。
ρ
(
X
,
Y
)
\rho (X,Y)
ρ(X,Y)计算公式:
ρ
(
X
,
Y
)
=
2
n
(
n
−
1
)
∑
i
<
j
s
g
n
(
x
i
−
x
j
)
s
g
n
(
y
i
−
y
j
)
\rho (X,Y) =\frac{2}{n(n - 1)} \sum_{i<j}sgn(x_i - x_j)sgn(y_i - y_j)
ρ(X,Y)=n(n−1)2i<j∑sgn(xi−xj)sgn(yi−yj)
其中,
s
g
n
(
⋅
)
sgn(\cdot)
sgn(⋅)为符号函数。
取值范围为[-1, 1]。在显著性的前提下,绝对值越大,相关性越强。
ρ
(
X
,
Y
)
>
0
\rho (X,Y)>0
ρ(X,Y)>0:表示变量X, Y正相关;
ρ
(
X
,
Y
)
<
0
\rho (X,Y)<0
ρ(X,Y)<0:表示变量X, Y负相关;
ρ
(
X
,
Y
)
=
0
\rho (X,Y)=0
ρ(X,Y)=0:表示变量X, Y相互独立;
∣
ρ
(
X
,
Y
)
∣
=
1
|\rho (X,Y)|=1
∣ρ(X,Y)∣=1:表示变量X, Y完全相关。
适用条件:
与变量的总体分布无关,样本集容量也不要求大于30。
3 度量分布
3.1 直方图(Histogram)
直方图是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据的类型,纵轴表示分布情况。
直方图的数据也可以视为一个向量,每一个维度代表数据的一个类型,维度上的取值代表该类型的分布情况。
注意这个向量表示,在机器学习中较多使用该向量表示,而不是直接使用图形表示。
直方图是数值数据分布的精确图形表示。 这是一个连续变量(定量变量)的概率分布的估计,并且被卡尔·皮尔逊(Karl Pearson)首先引入。
直方图数据的计算方法:
给定集合A。如果元素是连续的数值,则集合A中的所有元素进行离散化处理,所有可能的元素值都映射到有限个区间上,为这些区间建立索引名称,这有限个索引上。如果元素是离散的值,则可以直接将这些元素值作为索引名称(如果取值较多仍然可以继续分类进一步构建分类索引)。
这些索引通常有具体的含义,按照含义给他们排个顺序。用直方图表示就自然而然的了。
举例:
人的年龄是个连续值,我们可以离散化为各种年龄段,比如新国家标准里面定义的:婴儿(0-0.6岁)、幼儿(0.6-2岁)、儿童(3-6岁)、少年(7-14岁)、青年(15-35岁)、中年(36-60岁)、老年(61岁及以上),其中“婴儿、幼儿…老年”等这些即为索引名称。可以比较容易地统计出不同年龄段的人数比例分布,该分布反映了人群的老龄化程度。
用途
1.可以看百度百科:直方图,对用途场景有详细的介绍。
HOG特征、LBP特征提取算法中有用到直方图。详情可参考:图像特征提取三大法宝:HOG特征,LBP特征,Haar特征
缺点
集合A中的元素是无序的,直方图仅仅是度量该集合中数据的分布情况,无法同时度量出元素间的顺序、结构关系,因此对存在元素间顺序、结构关系的集合,可能要结合应用目的评估是否选用直方图度量方法。
3.2 偏度(skewness)
偏度度量的是某总体取值分布的对称性。
给定集合X,偏度定义为样本的三阶标准矩。
Skew
(
X
)
=
E
[
(
X
−
μ
σ
)
3
]
\operatorname{Skew}(X)=E\left[\left(\frac{X-\mu}{\sigma}\right)^{3}\right]
Skew(X)=E[(σX−μ)3]
其中,μ:样本均值,δ:标准差,E:均值。
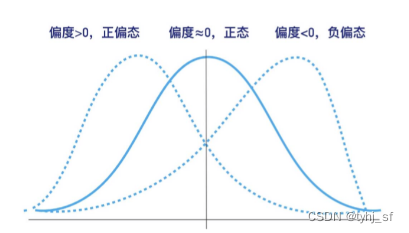
偏度=0:表示给定集合X的数据分布是正态分布;
偏度>0:表示给定集合X的数据分布相对于正态分布为右偏分布,即正偏态;
偏度<0:表示给定集合X的数据分布相对于正态分布为左偏分布,即负偏态。
3.3 峰度(Kurtosis)
峰度是描述总体中所有取值分布形态陡缓程度的统计量.
给定集合X,峰度定义为样本的四阶标准矩。
K
u
r
t
(
X
)
=
E
[
(
X
−
μ
σ
)
4
]
Kurt(X)=E\left[\left(\frac{X-\mu}{\sigma}\right)^{4}\right]
Kurt(X)=E[(σX−μ)4]
其中,μ:样本均值,δ:标准差,E:均值。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
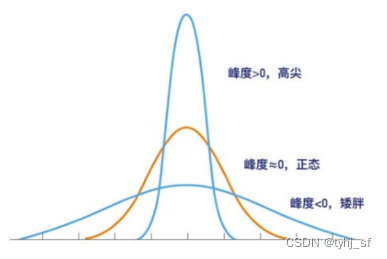
峰度=0:表示给定集合X的数据分布与正态分布的陡缓程度相同;
峰度>0:表示给定集合X的数据分布与正态分布相比较为陡峭,为尖顶峰;
峰度<0:表示给定集合X的数据分布与正态分布相比较为矮胖,为平顶峰。
3.4 雅克-贝拉检验(Jarque-Bera)
雅克-贝拉检验是对样本数据是否具有符合正态分布的偏度和峰度的拟合优度的检验。该检验以卡洛斯·哈尔克和阿尼·K·贝拉(Carlos Jarque and Anil K. Bera)来命名。
给定样本集合X,构造统计量
J
B
(
X
)
JB(X)
JB(X):
J
B
(
X
)
=
n
(
S
2
6
+
(
K
−
3
)
2
24
)
JB(X)=n( \frac{S^2}{6}+\frac{(K−3)^2}{24})
JB(X)=n(6S2+24(K−3)2)
其中:n为样本规模,S、K分别为集合X的偏度和峰度。
原假设H0:样本服从正态分布,来自一个正态分布的总体,那么JB(X)渐近于χ(2)分布;
备择假设H1:样本不服从正态分布。
JB(X)总是非负的。如果结果远大于零,则表示数据不具有正态分布。
注:Jarque-Bera检验不能用于小样本检验。
4 度量位置
需要注意的是,此处所致位置是泛指而不是特指三维空间中的位置。比如,在自然语言中,对象即词语,位置即词语的语义,词语的含义由上下文语境唯一确定。
正如《马克思论费尔巴哈》中说的“人是一切社会关系的总和”,度量的对象也存在于其所属集合中,我们姑且可以粗暴地给出一个假设:对象在集合中的位置是对象的上下文关系的总和。
4.1 直方图的向量
直方图数据的向量表示形式就是很好的度量位置的方法。
在上文3.1节中已有介绍,不再赘述。
4.2 Embedding方法
来自于自然语言处理领域,Embedding方法即词嵌入方法,比如TF-IDF、Word2Vec等方法。通过词在语料库特定上下文信息训练出每个词的词向量,这是词在语义空间中的位置。明白Embedding方法这一原理,迁移到其他领域,“万物皆可Embedding”。
参考资料
[1].交叉熵、相对熵(KL散度)的数学原理及在机器学习中应用.
[2].Pearson, Spearman, Kendall 三大相关系数简单介绍
[3].https://reference.wolfram.com/language/guide/DistanceAndSimilarityMeasures.html
![[附源码]JAVA毕业设计课程网站设计(系统+LW)](https://img-blog.csdnimg.cn/2078b5936965487b8d4c6aa0d95c7a9c.png)

![[论文阅读] 颜色迁移-直方图渐进式颜色迁移](https://img-blog.csdnimg.cn/2019ed3efde3497ca248c59b58453b6f.png)


![[Swift]国际化](https://img-blog.csdnimg.cn/daf1fd7f1129445f89a70915de907298.png)
![[附源码]Python计算机毕业设计SSM景区在线购票系统(程序+LW)](https://img-blog.csdnimg.cn/1fc9988db0ce450cb633309d5a8d0aa4.png)

![[附源码]计算机毕业设计共享汽车系统](https://img-blog.csdnimg.cn/b9064a9c59b5458080d83925e206f0d8.png)