目录
二叉搜索树的性质
二叉搜索树的实现
结点类
接口类(BSTree)
二叉搜索树的插入(insert)
二叉搜索树的查找(find)
二叉搜索树删除(erase)
第二种、删除的结点右子树为空
第三种、删除的结点左子树为空
第四种、删除的结点左右都不为空
实现
二叉搜索树模拟实现代码总结
二叉搜索树的缺陷
缺陷
解决办法:
二叉搜索树的性质
二叉搜索树正如其名,底层是一个二叉树
二叉搜索树的每一颗左子树小于根节点的值
二叉搜索树的每一颗右子树大于根节点的值
二叉搜索树的结点中的值不能重复!
如图所示,即为一颗二叉搜索树

也正因为以上两条的性质,那么我们在二叉搜索树中进行查找时,时间复杂度是高度次
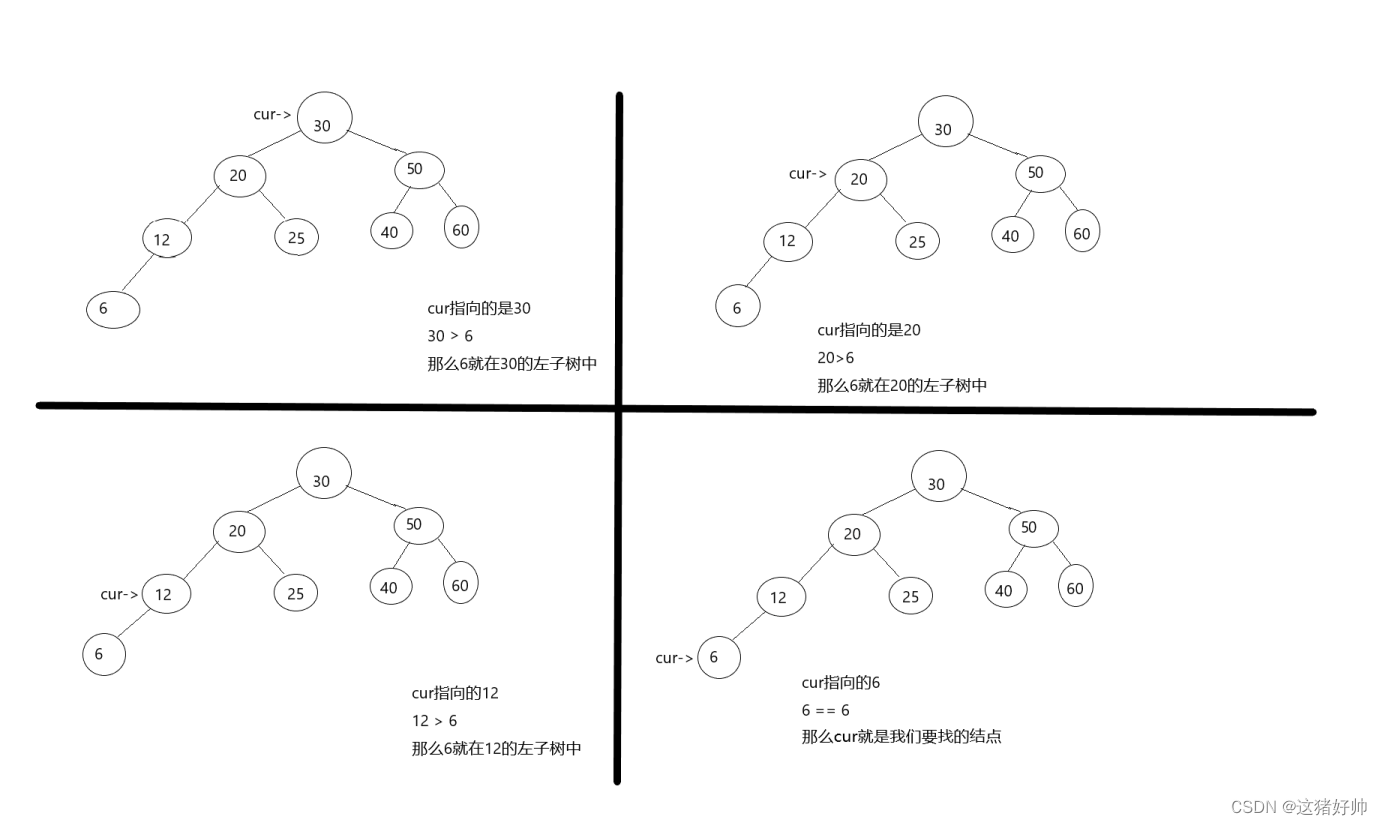
如下是在一颗二叉搜索树中查找元素6的过程
二叉搜索树的中序遍历完后就是有序序列

如图中序遍历为:6,20,25,30,40,50,60
二叉搜索树的实现
结点类
二叉搜索树我们使用三叉链来实现
三叉链:需要一个父指针,左孩子指针,右孩子指针
template<class T>
struct BSTreeNode
{
BSTreeNode<T>* _left;
BSTreeNode<T>* _right;
BSTreeNode<T>* _parent;
T _data;
BSTreeNode(const T& data)
:_data(data)
,_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
{
}
};接口类(BSTree)
二叉搜索树的接口类和list的接口类差不多,
list存储的是一个头节点,二叉搜索树存储的是一个根节点
template<class T>
class BSTree
{
typedef BSTreeNode<T> Node;
public:
//接口实现
private:
//给个缺省参数为空,后续就不用写构造函数了
Node* _root = nullptr;
};二叉搜索树的插入(insert)

二叉搜索树的插入,只要结点中的值不发生重复,那么就一定是插入到树的叶子结点
如图
如果我们插入一个1,则在结点6的左边,返回true
如果我们插入一个23,则在结点25的左边,返回true
但如果我们插入一个30,与结点中的值重复则不插入,返回false
我们先看看插入一个23的过程图
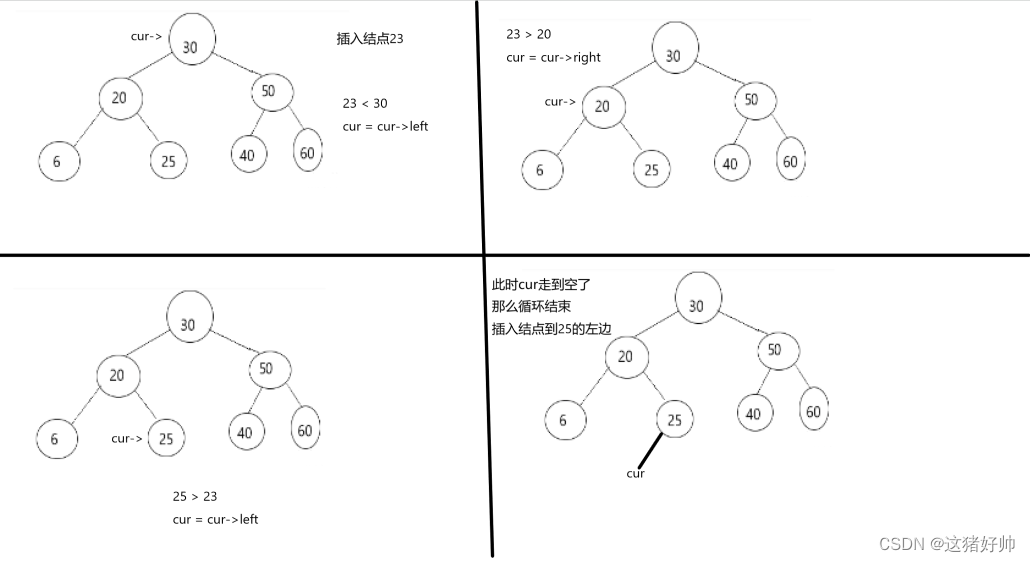
但上面这个过程中有一个问题,那就是cur最终会走到空,但空指针没办法访问
如果我们不记录cur的父节点的话,最终当cur走到空时,无法判断它的父节点是谁,最终无法链接
所以我们在插入时还需要有一个parent指针,那么代码实现如下:
bool insert(const T& x)
{
Node* cur = _root;//用来遍历的结点
Node* parent = nullptr;//记录cur的父节点
while(cur)
{
//_data 是Node的值
if(x > cur->_data)
{
parent = cur;
cur = cur->_right;
}
else if(x < cur->_data)
{
parent = cur;
cur = cur->_left;
}
else
{
//走到这里就说明x == cur->_data
//要插入的值已经在树中存在
return false;
}
}
//创建结点
Node* ret = new Node(x);
//把结点插入树中
if (cur == _root)
{
//特殊情况,当树中一个结点都没,那么cur不会进入循环
//此时parent为空
_root = ret;
return true;
}
if(ret->_data > parent->_data)
{
parent->_right = ret;
}
else
{
parent->_left = ret;
}
ret->_parent = parent;
return true;
}二叉搜索树的查找(find)
Node* find(const T& x)
{
Node* cur = _root;
while(cur)
{
if(cur->_data < x)
{
//查找的值比当前结点的值要大
cur = cur->_right;
}
else if(cur->_data > x)
{
//查找的值比当前结点的值要小
cur = cur->_left;
}
else
{
//找到了
return cur;
}
}
//cur为空,树里面没有这个值
return nullptr;
}二叉搜索树删除(erase)
二叉搜索树的删除就稍微复杂一点,一共分为3种情况
这一种情况很简单,我们只需改变其父节点指向删除结点的指针为空,再释放删除结点即可
注意:当树中只有一个结点时它父节点为空,如果我们访问父节点就会报错,所以我们要针对树中只有一个结点的情况特殊处理
bool EraseZero(Node* cur)
{
if (cur == _root)
{
//这里专门处理只有一个根节点的情况
delete cur;
_root = nullptr;
return true;
}
Node* parent = cur->_parent;
if(parent->_left == cur)
{
parent->_left = nullptr;
}
else
{
parent->_right = nullptr;
}
delete cur;
return true;
}第二种、删除的结点右子树为空
如图所示

假设我们要删除图上的值为60的结点
第一步:先找到这个结点
第二步:找到这个结点的父亲结点和左孩子结点,并记录下来
第三步:删除这个结点
第四步:让这个左孩子结点顶替这个结点的父亲结点的右孩子位置
注意:如图这种情况下,删除值为30的结点,但这个结点是根节点没有父亲结点,所以对这种情况特殊处理一下

第三种、删除的结点左子树为空
左子树为空的处理方法可以归并为右子树为空的情况,简直一摸一样
那么我们就可以写一个接口把这两种情况都囊盖了
bool EraseOne(Node* cur)
{
if(_root == cur)
{
Node* ret = cur->_left == nullptr ? cur->_right : cur->_left;
delete cur;
_root = ret;
return true;
}
Node* parent = cur->_parent;
Node* ret = cur->_left == nullptr ? cur->_right : cur->_left;
if(parent->_left == cur)
{
parent->_left = ret;
}
else
{
parent->_right = ret;
}
ret->_parent = parent;
delete cur;
return true;
}第四种、删除的结点左右都不为空
这一种情况当我们在进行删除时需要找到这个结点的替代结点
替代结点一定有至少一个孩子结点为空
当我们替换完以后此时的二叉搜索树必须还保持着它的性质
替换节点有两种选择
第一种、删除结点的左孩子的最右结点
第二种、删除结点的右孩子的最左结点
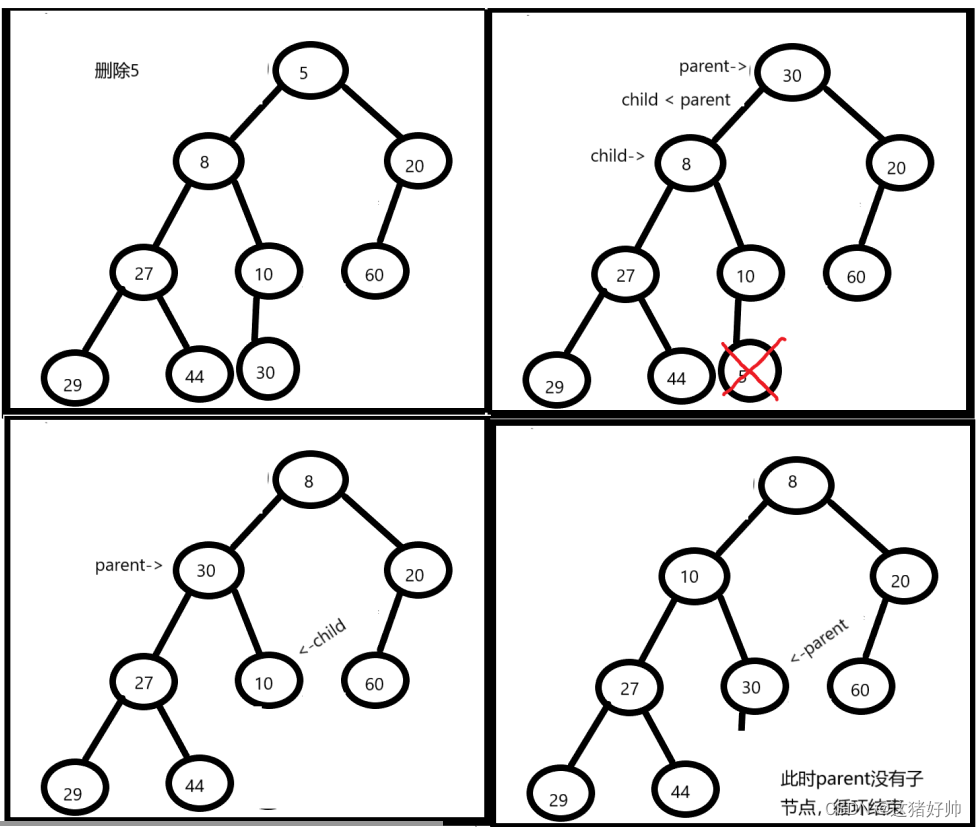
如图,假如我们要删除值为30的结点
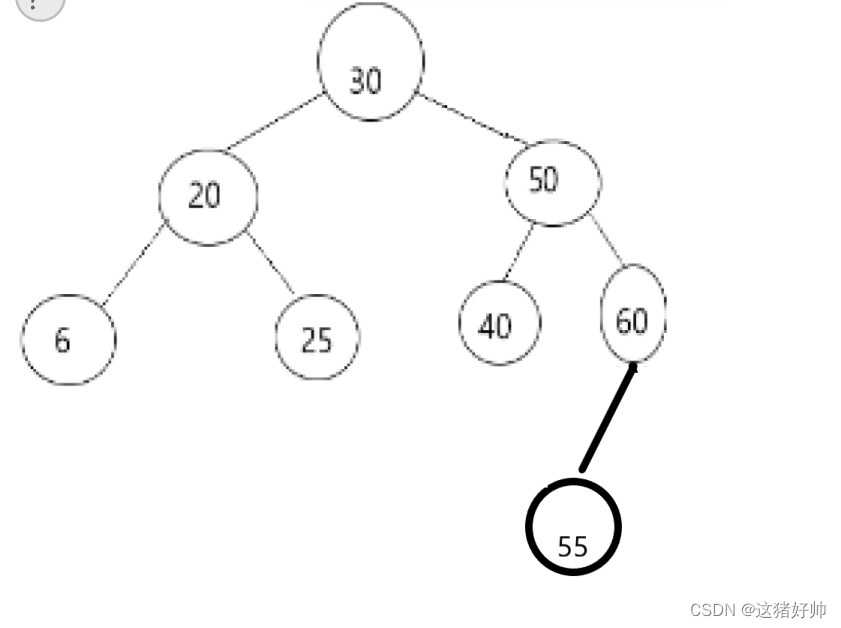
替换结点为红圈圈起来的两个
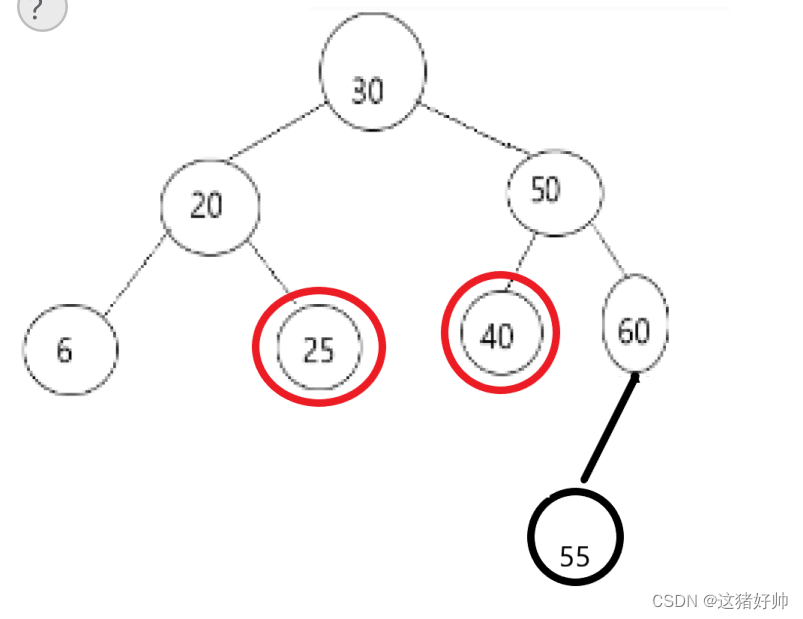
我们实现的话就采用第一种选用替换结点的方式
当我们替换完以后如图

我们就把删除左右子树都不为空的情况转化为了左右子树都为空的情况
我们再来看一张图,此时如果我们要删除25:红圈圈起来的是替换节点
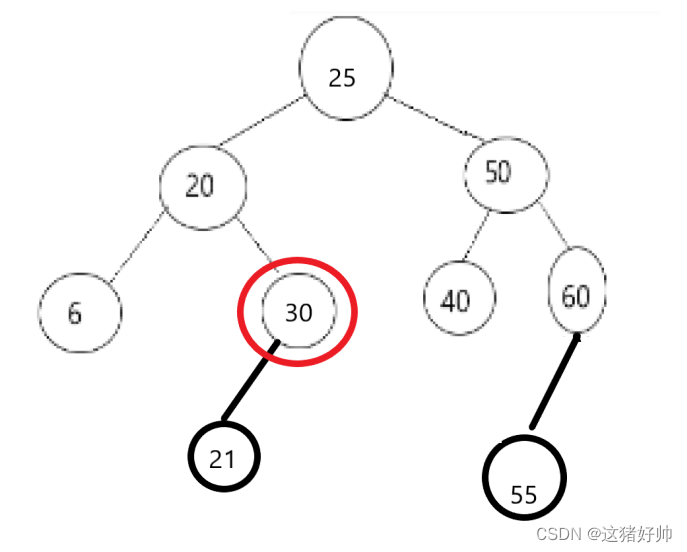
交换删除结点与替换结点
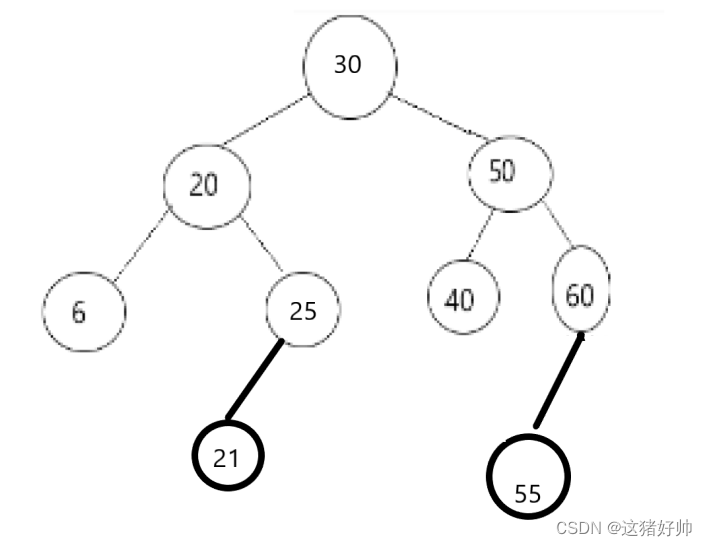
可以看到,此时就由删除一个左右子树都不为空的结点变成了删除至少有一颗树为空的结点
bool EraseTwo(Node* cur)
{
//1、找到替代结点
Node* tmp = cur->_left;
while(tmp->_right)
{
tmp = tmp->_right;
}
std::swap(cur,tmp);
if(cur->_left == nullptr && cur->_right == nullptr)
{
//复用情况1
return EraseZero(cur);
}
else
{
//复用情况2、3
return EraseOne(cur);
}
}实现
bool erase(const T& x)
{
if(!find(x))
{
//删除的结点不存在
return false;
}
Node* cur = _root;
while(cur)
{
if(cur->_data > x)
{
cur = cur->_left;
}
else if(cur->_data < x)
{
cur = cur->_right;
}
else
{
//找到了要删除的结点
break;
}
}
//理论上cur此时一定是break出来的,那么到这里我们就开始分情况讨论了
if(cur->_left == nullptr && cur->_right == nullptr)
{
return EraseZero(cur);
}
if(cur->_left && cur->_right)
{
return EraseTwo(cur);
}
else if(cur->_left != nullptr || cur->_right != nullptr)
{
return EraseOne(cur)
}
}二叉搜索树模拟实现代码总结
template<class T>
struct BSTreeNode
{
BSTreeNode<T>* _left;
BSTreeNode<T>* _right;
BSTreeNode<T>* _parent;
T _data;
BSTreeNode(const T& data)
:_data(data)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
{
}
};
template<class T>
class BSTree
{
typedef BSTreeNode<T> Node;
public:
//接口实现
bool insert(const T& x)
{
Node* cur = _root;//用来遍历的结点
Node* parent = nullptr;//记录cur的父节点
while (cur)
{
//_data 是Node的值
if (x > cur->_data)
{
parent = cur;
cur = cur->_right;
}
else if (x < cur->_data)
{
parent = cur;
cur = cur->_left;
}
else
{
//走到这里就说明x == cur->_data
//要插入的值已经在树中存在
return false;
}
}
//创建结点
Node* ret = new Node(x);
//把结点插入树中
if (cur == _root)
{
//特殊情况,当树中一个结点都没,那么cur不会进入循环
//此时parent为空
_root = ret;
return true;
}
if (ret->_data > parent->_data)
{
parent->_right = ret;
}
else
{
parent->_left = ret;
}
ret->_parent = parent;
return true;
}
Node* find(const T& x)
{
Node* cur = _root;
while (cur)
{
if (cur->_data < x)
{
//查找的值比当前结点的值要大
cur = cur->_right;
}
else if (cur->_data > x)
{
//查找的值比当前结点的值要小
cur = cur->_left;
}
else
{
//找到了
return cur;
}
}
//cur为空,树里面没有这个值
return nullptr;
}
bool erase(const T& x)
{
Node* cur = _root;
while (cur)
{
if (cur->_data > x)
{
cur = cur->_left;
}
else if (cur->_data < x)
{
cur = cur->_right;
}
else
{
//找到了要删除的结点
break;
}
}
//到这里我们就开始分情况讨论了
if (cur == nullptr)
{
//没有这个结点
return false;
}
if (cur->_left == nullptr && cur->_right == nullptr)
{
return EraseZero(cur);
}
else if (cur->_left && cur->_right)
{
return EraseTwo(cur);
}
else
{
return EraseOne(cur);
}
}
void Print()
{
_Print(_root);
std::cout << std::endl;
}
private:
void _Print(Node* cur)
{
if (cur == nullptr)
{
return;
}
_Print(cur->_left);
std::cout << cur->_data << " ";
_Print(cur->_right);
}
bool EraseZero(Node* cur)
{
if (cur == _root)
{
//这里专门处理只有一个根节点的情况
delete cur;
_root = nullptr;
return true;
}
Node* parent = cur->_parent;
if (parent->_left == cur)
{
parent->_left = nullptr;
}
else
{
parent->_right = nullptr;
}
delete cur;
return true;
}
bool EraseOne(Node* cur)
{
if (_root == cur)
{
Node* ret = cur->_left == nullptr ? cur->_right : cur->_left;
delete cur;
_root = ret;
return true;
}
Node* parent = cur->_parent;
Node* ret = cur->_left == nullptr ? cur->_right : cur->_left;
if (parent->_left == cur)
{
parent->_left = ret;
}
else
{
parent->_right = ret;
}
ret->_parent = parent;
delete cur;
return true;
}
bool EraseTwo(Node* cur)
{
//1、找到替代结点
Node* tmp = cur->_left;
while (tmp->_right)
{
tmp = tmp->_right;
}
std::swap(cur, tmp);
if (cur->_left == nullptr && cur->_right == nullptr)
{
//复用情况1
return EraseZero(cur);
}
else
{
//复用情况2、3
return EraseOne(cur);
}
}
private:
//给个缺省参数为空,后续就不用写构造函数了
Node* _root = nullptr;
};二叉搜索树的缺陷
缺陷
二叉搜索树在普通情况下没有什么明显的缺陷
不过在极端情况下二叉搜索树效率会降低(甚至退化成链表)
如图:

这个二叉搜索树可以看到,有5个结点,却有三层,我们都知道二叉搜索树的效率是高度次
那么如果我们再极端一点,插入一个有序数组,此时查找的时间复杂度就来到了O(n)
如图为插入一个有序数组(1,2,3,4,5,6,7,8)后的二叉搜索树
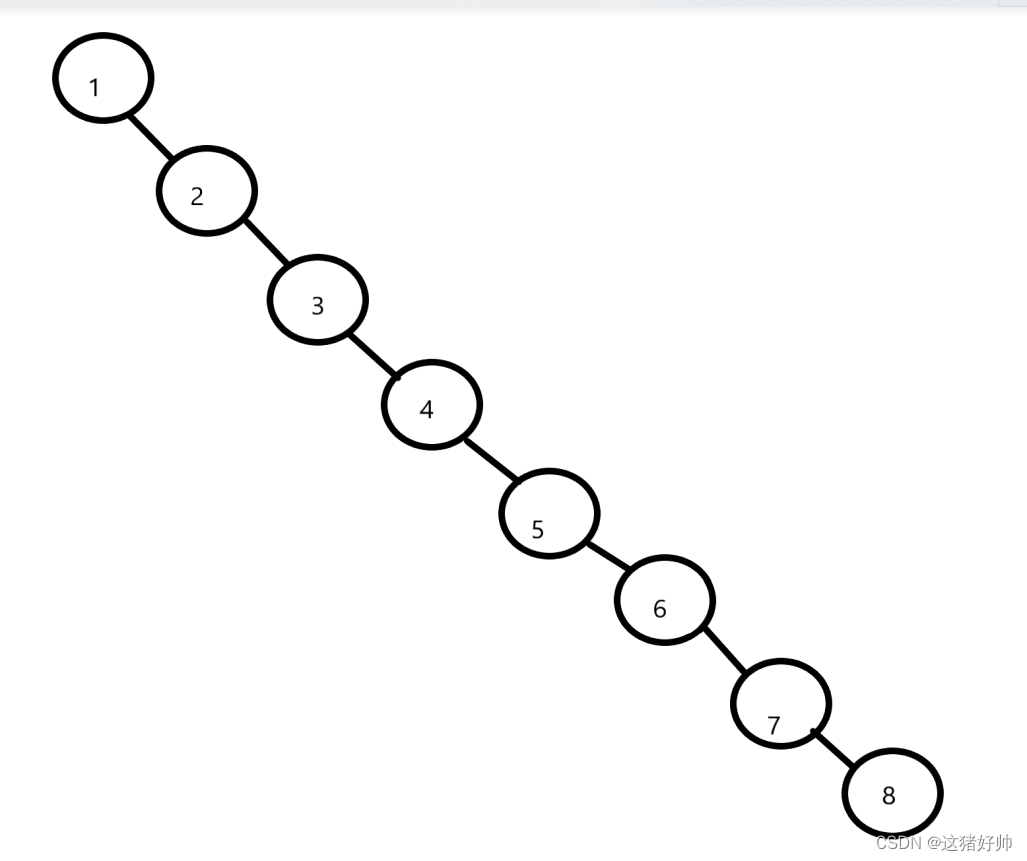
可以看到,此时二叉搜索树就退化成了链表
解决办法:
下一期我们会介绍一个数据结构叫做(AVL树)也叫做高度平衡的二叉搜索树,它就完美解决了如上的问题
那么这一期就到这了,感谢大家的支持