高度平衡二叉搜索树(AVLTree)（插入与旋转）

news2024/7/2 3:49:58

 

目录

简介

AVL的结点类

平衡因子的性质

AVL树的插入 

更新平衡因子的接口(ChangeBf)

第一种情况：插入后父节点的平衡因子为0

第二种情况：更新后父节点的平衡因子的绝对值为1

第三种情况：更新后父节点的平衡因子的绝对值为2

旋转接口(Rotate)

左单旋(RotateL)

右单旋(RotateR)

右左双旋(RotateRL)

 左右双旋(RotateLR)

简介

AVL树是基于我们上一期讲过的二叉搜索树改变而来，如果没有看过我上一期博文的可以先看看

这一期的代码也是基于上一章的基础上而来的

二叉搜索树

AVL树就是在二叉搜索树的基础上进行控制左右子树高度差的绝对值不超过1

 而我们接下来所讲的实现方式加入了平衡因子(bf)

其实AVL树的查找与二叉搜索树的查找是一样的，他们之间的差别在于插入与删除

而本节内容就针对AVL树的插入来展开

话不多说我们正式进入正题

AVL的结点类

在我们实现插入接口之前我们先看看AVL的结点类

结点类与二叉搜索树的结点类大致相同，只是在其中新添了一个平衡因子

平衡因子的性质

当平衡因子大于-1小于1时表示的是这个结点是平衡的

当平衡因子大于1或小于-1时表示这个结点是不平衡的

平衡因子的计算：右子树的高度-左子树的高度就是这个结点的平衡因子

改造后的结点类如下：

template<class T>
struct AVLTreeNode
{
    int _bf;//新增的平衡因子
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;
    AVLTreeNode<T>* _parent;
    T _data;
     AVLTreeNode(const T& x)
         :_bf(0)
         ,_left(nullptr)
         ,_right(nullptr)
         ,_parent(nullptr)
         ,_data(x)
    {
    }
};

AVL树的插入 

 bool insert(const T& x)
    {
        Node* cur = _root;
        Node* parent = nullptr;
        while (cur)
        {
            if (cur->_data < x)
            {
                parent = cur;
                cur = cur->_right;
                //结点的值 < 插入的值
            }
            else if (cur->_data > x)
            {
                parent = cur;
                cur = cur->_left;
                //结点的值 > 插入的值
            }
            else
            {
                //结点的值 = 插入的值
                return false;
            }
        }
        if(cur == _root)
        {
            _root = new Node(x);
            return true;
        }
        cur = new Node(x);
        if (parent->_data > x)
        {
            //连在parent的左边
            parent->_left = cur;
        }
        else
        {
            //连在parent的右边
            parent->_right = cur;
        }
        cur->_parent = parent;
        ChangeBf(cur);//更新平衡因子的接口
        return true;
    }

如上代码，与二叉搜索树的插入逻辑是一样的

二叉搜索树的插入

接下来，我们要完成的是平衡因子更新的接口

更新平衡因子的接口(ChangeBf)

首先，根据AVL树的性质我们知道左右子树的高度差的绝对值不能超过1

平衡因子的计算公式为：右子树高度-左子树高度

那么我们在一颗AVL树中插入节点后其父节点平衡因子的可能取值就有五种：0，-1，1，-2，2

第一种情况：插入后父节点的平衡因子为0

如图：(节点旁标注为平衡因子)

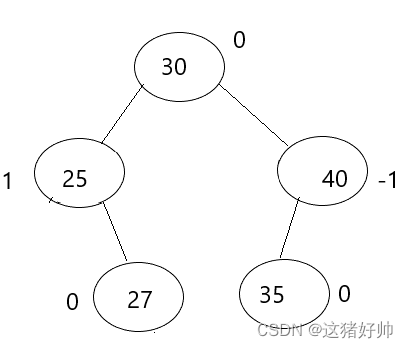
如果在这一张图中我们想要让父节点的平衡因子为0，那么插入的位置就一定为40的左边或25的右边

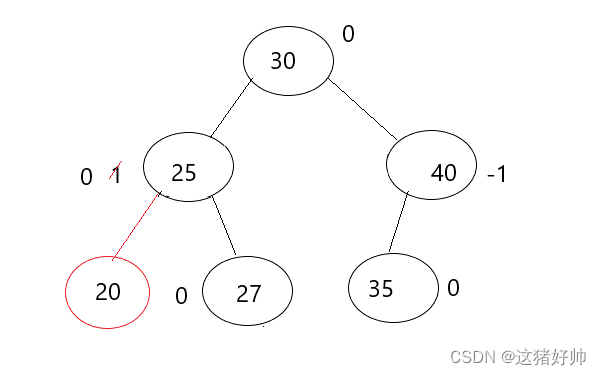
 我们仔细观察如果我们想要插入后其父节点平衡因子更新为0，那么在我们插入之前父节点的平衡因子的绝对值要为1，也就是左右子树一边高一边低

而只要平衡因子更新为0后，说明插入后把父节点的左右子树高度变为一致了，此时不会再影响父节点往上的节点的左右子树高度差，因为父节点以上的节点的高度并没有发生改变

第二种情况：更新后父节点的平衡因子的绝对值为1

这一种情况的发生只会出现在父节点在更新前的平衡因子为0，也就是父节点在插入时左右子树高度相同

如果我们此时在父节点的左边插入，此时平衡因子为-1(左边高)

如果我们此时在父节点的右边插入，此时平衡因子为1(右边高)

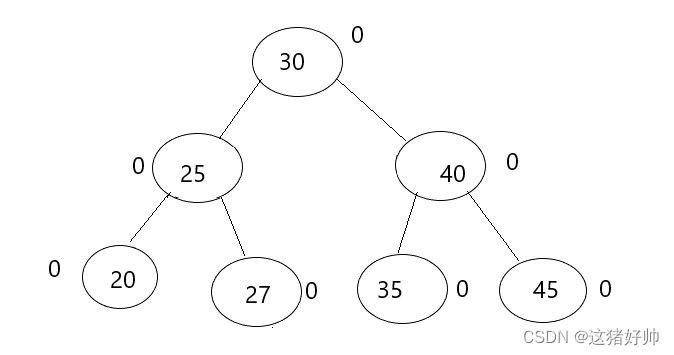
 如图我们在45的右边插入一个数据试试：

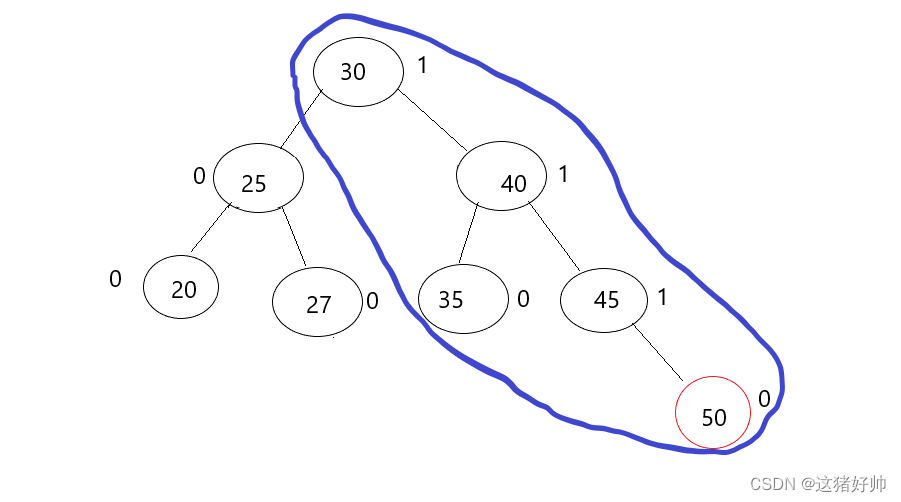
 我们可以看到，标蓝圈所在的所有节点的平衡因子都发生了改变，原因如下

 50这个节点是作为45节点的右子树（我们45所在的这棵树单独叫做A树）

40的右子树为A树，A树高度发生了改变，40这棵树的高度也发生了改变(我们把40这棵树叫做B树)

30这棵树的右子树为B树，B树的高度发生了改变，30的高度也会发生改变

结论：当插入后父节点的绝对值为1，直至更新到根节点或者更新到祖宗结点的平衡因子为0(左右子树高度相等)才停止更新

第三种情况：更新后父节点的平衡因子的绝对值为2

如果我们更新后父节点的平衡因子绝对值为2，说明父节点所在子树已经不是AVL树了，需要马上进行旋转处理

void ChangBf(Node* cur)
{
    Node* parent = cur->_parent;
    if(cur == root)
    {
        return;
    }
    else
    {
        while(parent)
        {
            //先更新parent的bf
            if(cur == parent->_left)
            {
                --parent->_bf;
            }
            else
            {
                ++parent->_bf;
            }

            //到这里要进行判断parent的bf，确定是否向上更新
            if(parent->_bf == 0)
            {
                break;
            }
            else if(abs(parent->_bf) == 1)
            {
                //继续向上更新
                cur = parent;
                parent = parent->_parent;
            }
            else if(abs(parent->_bf) == 2)
            {
                //进行旋转处理
                Rotate(parent);
                break;
            }
            else
            {
                //理论上来说，不可能走到这里
                assert(false);
            }
        }
    }
}

旋转接口(Rotate)

如果父节点平衡因子为2，且右孩子节点的平衡因子为1，说明此时右边高，我们需要进行左单旋处理

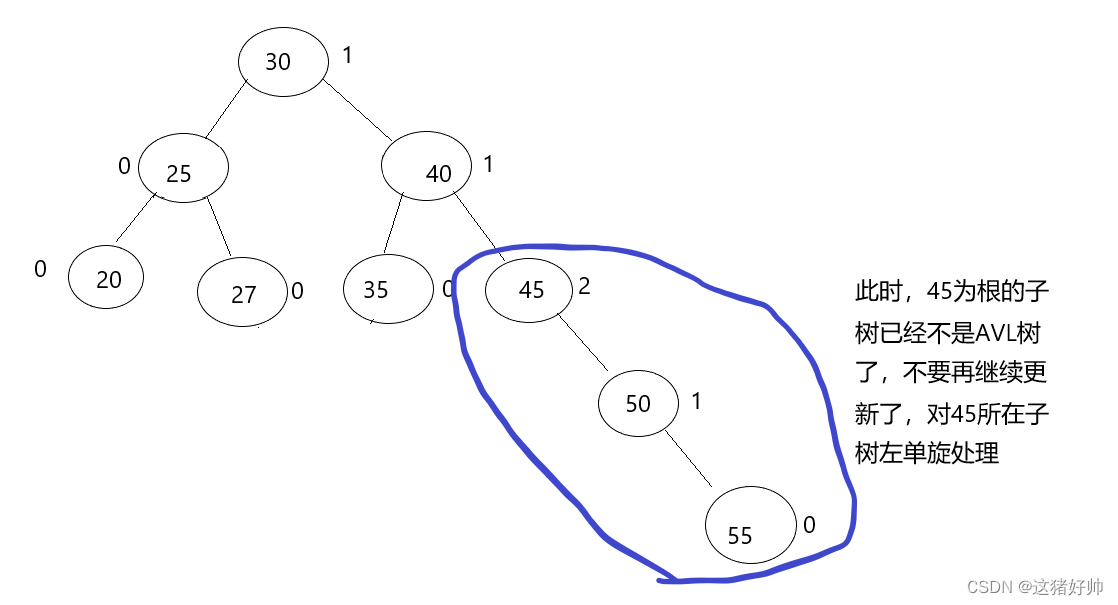
 如果父节点平衡因子为-2，且左孩子节点的平衡因子为-1，说明此时左边高，我们需要进行右单旋处理

 如果父节点的平衡因子为2，且右孩子节点的平衡因子为-1，此时要进行右左双旋处理

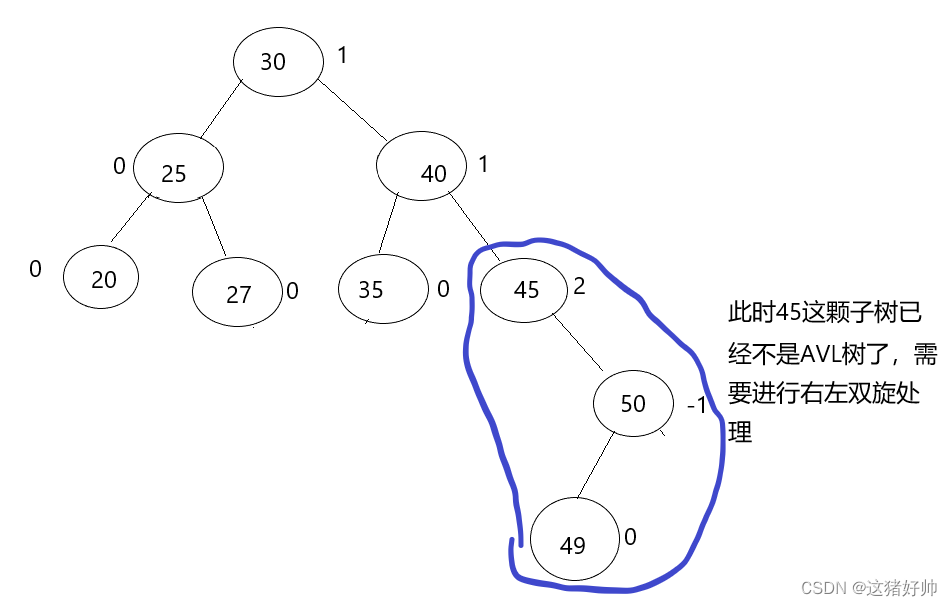
 如果父节点的平衡因子为-2，且左孩子节点的平衡因子为1，此时要进行左右双旋处理，如图

Rotate接口代码实现

void Rotate(Node* cur)
{
    if(cur->_bf == 2 && cur->_right->_bf == 1)
    {
        //左单旋
        RotateL(cur);
    }
    else if(cur->_bf == 2 && cur->_right->_bf == -1)
    {
        //右左双旋
        RotateRL(cur);
    }
    else if(cur->_bf == -2 && cur->_left->_bf == -1)
    {
        //右单旋
        RotateR(cur);
    }
    else if(cur->_bf == -2 && cur->_left->_bf == 1)
    {
        //左右双旋
        RotateLR(cur);
    }
    else
    {
        //理论上来说，不可能走到这
        assert(false);
    }
}

左单旋(RotateL)

抽象图如下(h为高度)：

 

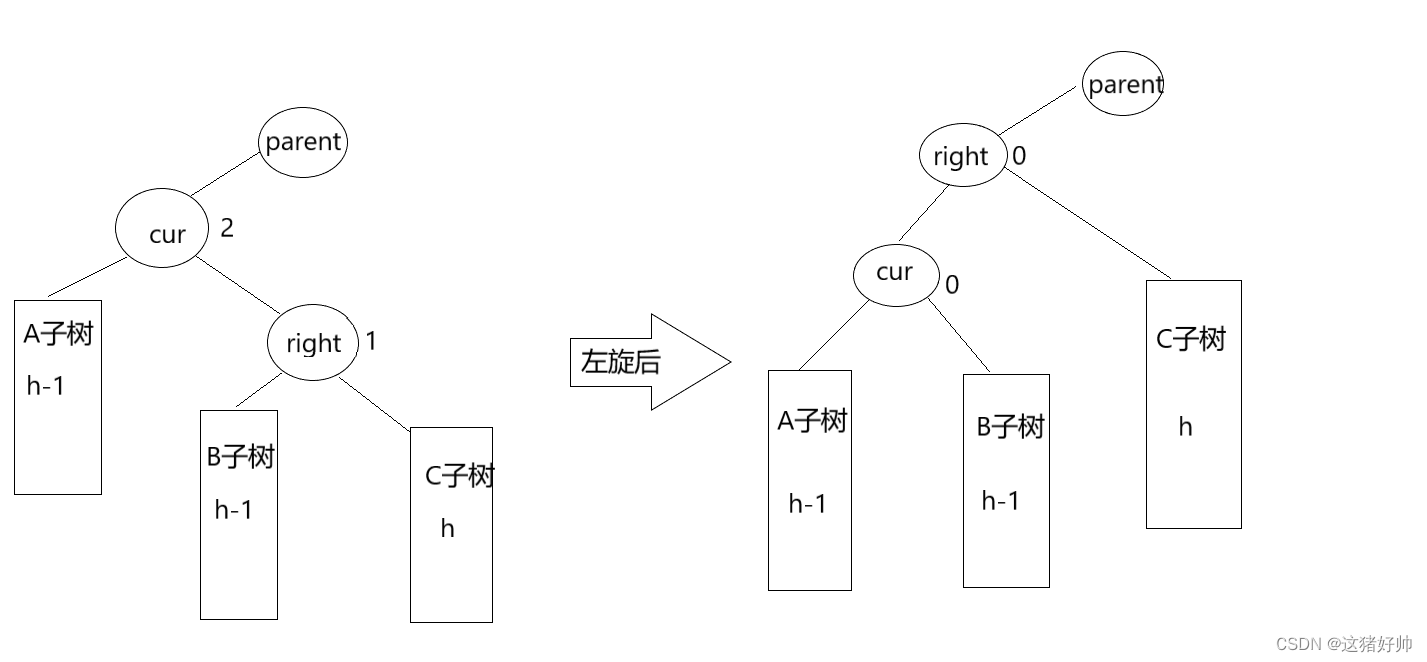
 我们可以看到，左单旋操作改变的指针有6个

分别为：

cur的right指针

cur的parent指针

right的left指针

right的parent指针

parent原本指向cur的指针(parent可能为空，要进一步判断)

B子树的parent指针(B子树可能为空，要进一步判断)

void RotateL(Node* cur)
{
  Node* parent = cur->_parent;
  Node* curR = cur->_right;
  Node* curRL = curR->_left;
  cur->_right = curRL;
  cur->_parent = curR;

  curR->_left = cur;
  curR->_parent = parent;

  if (curRL)
    curRL->_parent = cur;

  if(cur != _root)
  {
            if (parent->_left == cur)
            {
                parent->_left = curR;
            }
            else
            {
                parent->_right = curR;
            }
  }
  else
  {
            _root = curR;
  }

  //更新平衡因子
  cur->_bf = curR->_bf = 0;
}

右单旋(RotateR)

抽象图如下(h为高度)：

 我们可以看到，右单旋改变的指针个数也为6个

分别为：

cur的parent指针

cur的left指针

left的parent指针

left的right指针

parent原本指向cur的指针(parent可能为空，要进一步判断)

B子树的parent指针(B子树可能为空，要进一步判断)

void RotateR(Node* cur)
    {
        Node* parent = cur->_parent;
        Node* curL = cur->_left;
        Node* curLR = curL->_right;
        cur->_parent = curL;
        cur->_left = curLR;
        curL->_parent = parent;
        curL->_right = cur;
        if (curLR)
            curLR->_parent = cur;
        if (cur == _root)
        {
            _root = curL;
        }
        else
        {
            if (parent->_left == cur)
            {
                parent->_left = curL;
            }
            else
            {
                parent->_right = curL;
            }
        }
        //更新平衡因子
        cur->_bf = curL->_bf = 0;
    }

右左双旋(RotateRL)

右左双旋在结点的平衡因子为2且结点的右孩子结点的平衡因子为-1时旋转的

右左双旋：先右旋右孩子结点，再左旋结点

不过右左双旋的重点在于平衡因子的更新，它的平衡因子的更新还要看right的左结点(后面叫lright)的哪边高和哪边低或是一样高，分为三种情况

第一种情况：lright的左右子树一样高

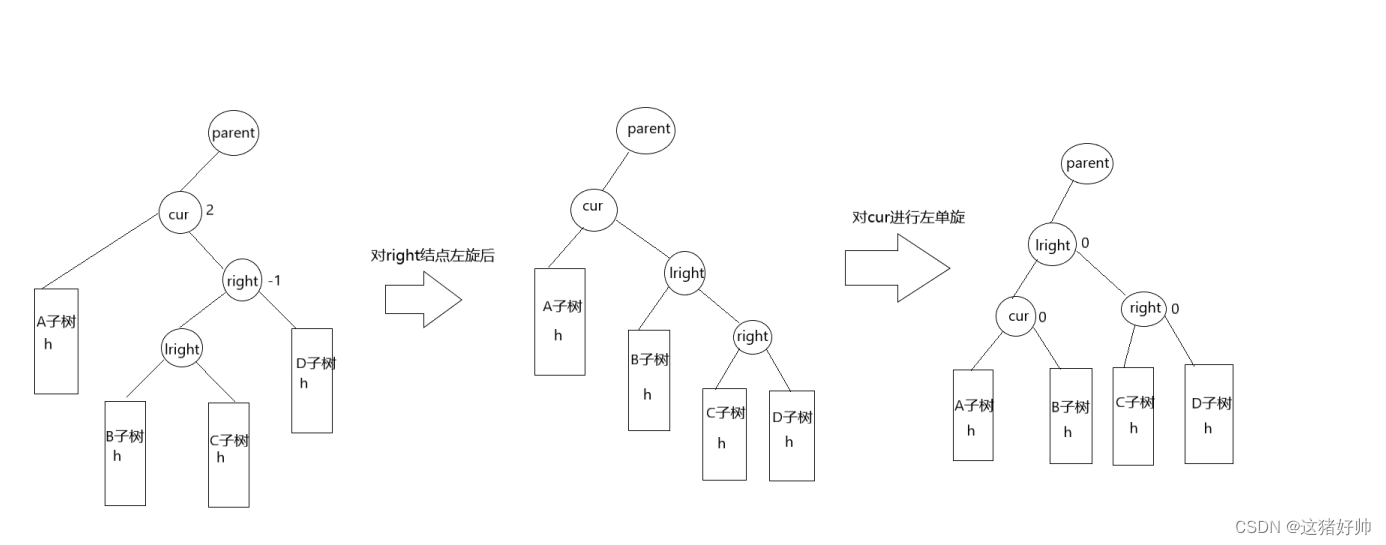
 可以看到，最终的平衡因子如图全为0

第二种情况：lright的左子树比右子树高

这种情况也对照上图可知，B子树为h，C子树为h-1

cur的平衡因子为0

right的平衡因子为-1

lright的平衡因子为0

第三种情况：lright的右子树比左子树高

这种情况对照上图即为B子树为h-1，C子树为h

cur的平衡因子为1

right的平衡因子为0

lright的平衡因子为0

    void RotateRL(Node* cur)
    {
        Node* curR = cur->_right;
        Node* curRL = curR->_left;
        int bf = curRL->_bf;
        RotateR(curR);
        RotateL(cur);
        if (bf == 0)
        {
            curRL->_bf = curR->_bf = cur->_bf = 0;
        }
        else if (bf == -1)
        {
            cur->_bf = curRL->_bf = 0;
            curR->_bf = 1;
        }
        else if (bf == 1)
        {
            curR->_bf = curRL->_bf = 0;
            cur->_bf = -1;
        }
    }

 左右双旋(RotateLR)

左右双旋在结点的平衡因子为-2且结点的左孩子结点的平衡因子为1时旋转的

左右双旋：先对左孩子结点左单旋，再对结点进行右单旋

同样左右双旋的重点在于平衡因子的更新，它的平衡因子的更新还要看left的右结点(后面叫rleft)的哪边高和哪边低或是一样高，分为三种情况

第一种情况：rleft的左右子树一样高

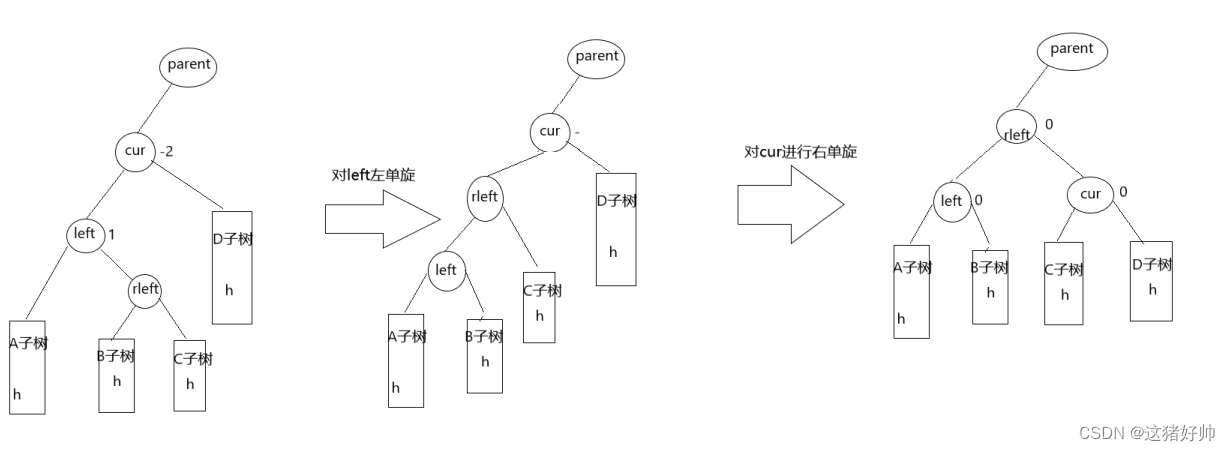
 可以看到，最终的平衡因子如图全为0

第二种情况：rleft的左子树比右子树高，B树高度为h，C树高度为h-1

left的平衡因子为0

cur的平衡因子为1

rleft的平衡因子为0

第三种情况：rleft的右子树比左子树高，B树高度为h-1，C树高度为h

left的平衡因子为-1

cur的平衡因子为0

rleft的平衡因子为0

    void RotateLR(Node* cur)
    {
        Node* curL = cur->_left;
        Node* curLR = curL->_right;
        int bf = curLR->_bf;
        RotateL(curL);
        RotateR(cur);
        if (bf == 0)
        {
            curLR->_bf = curL->_bf = cur->_bf = 0;
        }
        else if (bf == 1)
        {
            curL->_bf = -1;
            cur->_bf = curLR->_bf = 0;
        }
        else if (bf == -1)
        {
            cur->_bf = 1;
            curL->_bf = curLR->_bf = 0;
        }
    }

代码总结：

#pragma once
template<class T>
struct AVLTreeNode
{
    int _bf;//新增的平衡因子
    AVLTreeNode<T>* _left;
    AVLTreeNode<T>* _right;
    AVLTreeNode<T>* _parent;
    T _data;
    AVLTreeNode(const T& x)
        :_bf(0)
        , _left(nullptr)
        , _right(nullptr)
        , _parent(nullptr)
        , _data(x)
    {
    }
};

template<class T>
class AVLTree
{
    typedef AVLTreeNode<T> Node;
public:
    void Print()
    {
        _Print(_root);
    }
    void _Print(Node* cur)
    {
        if (!cur)
            return;

        _Print(cur->_left);
        std::cout << cur->_data << ":" << cur->_bf << " ";
        _Print(cur->_right);
    }
    bool insert(const T& x)
    {
        Node* cur = _root;
        Node* parent = nullptr;
        while (cur)
        {
            if (cur->_data < x)
            {
                parent = cur;
                cur = cur->_right;
                //结点的值 < 插入的值
            }
            else if (cur->_data > x)
            {
                parent = cur;
                cur = cur->_left;
                //结点的值 > 插入的值
            }
            else
            {
                //结点的值 = 插入的值
                return false;
            }
        }
        if (cur == _root)
        {
            _root = new Node(x);
            return true;
        }
        cur = new Node(x);
        if (parent->_data > x)
        {
            //连在parent的左边
            parent->_left = cur;
        }
        else
        {
            //连在parent的右边
            parent->_right = cur;
        }
        cur->_parent = parent;
        ChangeBf(cur);//更新平衡因子的接口
        return true;
    }
private:
    void ChangeBf(Node* cur)
    {
        Node* parent = cur->_parent;
        if (cur == _root)
        {
            return;
        }
        else
        {
            while (parent)
            {
                //先更新parent的bf
                if (cur == parent->_left)
                {
                    --parent->_bf;
                }
                else
                {
                    ++parent->_bf;
                }

                //到这里要进行判断parent的bf，确定是否向上更新
                if (parent->_bf == 0)
                {
                    break;
                }
                else if (abs(parent->_bf) == 1)
                {
                    //继续向上更新
                    cur = parent;
                    parent = parent->_parent;
                }
                else if (abs(parent->_bf) == 2)
                {
                    //进行旋转处理
                    Rotate(parent);
                    break;
                }
                else
                {
                    //理论上来说，不可能走到这里
                    assert(false);
                }
            }
        }
    }

    void Rotate(Node* cur)
    {
        if (cur->_bf == 2 && cur->_right->_bf == 1)
        {
            //左单旋
            RotateL(cur);
        }
        else if (cur->_bf == 2 && cur->_right->_bf == -1)
        {
            //右左双旋
            //RotateRL(cur);
        }
        else if (cur->_bf == -2 && cur->_left->_bf == -1)
        {
            //右单旋
            RotateR(cur);
        }
        else if (cur->_bf == -2 && cur->_left->_bf == 1)
        {
            //左右双旋
            //RotateLR(cur);
        }
        else
        {
            //理论上来说，不可能走到这
            assert(false);
        }
    }

    void RotateL(Node* cur)
    {
        Node* parent = cur->_parent;
        Node* curR = cur->_right;
        Node* curRL = curR->_left;
        cur->_right = curRL;
        cur->_parent = curR;
        curR->_left = cur;
        curR->_parent = parent;
        if (curRL)
            curRL->_parent = cur;
        if(cur != _root)
        {
            if (parent->_left == cur)
            {
                parent->_left = curR;
            }
            else
            {
                parent->_right = curR;
            }
        }
        else
        {
            _root = curR;
        }
        //更新平衡因子
        cur->_bf = curR->_bf = 0;
    }
    void RotateR(Node* cur)
    {
        Node* parent = cur->_parent;
        Node* curL = cur->_left;
        Node* curLR = curL->_right;
        cur->_parent = curL;
        cur->_left = curLR;
        curL->_parent = parent;
        curL->_right = cur;
        if (curLR)
            curLR->_parent = cur;
        if (cur == _root)
        {
            _root = curL;
        }
        else
        {
            if (parent->_left == cur)
            {
                parent->_left = curL;
            }
            else
            {
                parent->_right = curL;
            }
        }
        //更新平衡因子
        cur->_bf = curL->_bf = 0;
    }
    void RotateRL(Node* cur)
    {
        Node* curR = cur->_right;
        Node* curRL = curR->_left;
        int bf = curRL->_bf;
        RotateR(curR);
        RotateL(cur);
        if (bf == 0)
        {
            curRL->_bf = curR->_bf = cur->_bf = 0;
        }
        else if (bf == -1)
        {
            cur->_bf = curRL->_bf = 0;
            curR->_bf = 1;
        }
        else if (bf == 1)
        {
            curR->_bf = curRL->_bf = 0;
            cur->_bf = -1;
        }
    }
    void RotateLR(Node* cur)
    {
        Node* curL = cur->_left;
        Node* curLR = curL->_right;
        int bf = curLR->_bf;
        RotateL(curL);
        RotateR(cur);
        if (bf == 0)
        {
            curLR->_bf = curL->_bf = cur->_bf = 0;
        }
        else if (bf == 1)
        {
            curL->_bf = -1;
            cur->_bf = curLR->_bf = 0;
        }
        else if (bf == -1)
        {
            cur->_bf = 1;
            curL->_bf = curLR->_bf = 0;
        }
    }
protected:
    Node* _root = nullptr;
};

那么这一期内容就到这了，感谢大家的支持

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/617577.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

cam_lidar_calibration代码详解（一）采样优化部分

cam_lidar_calibration代码详解（一）采样优化部分

目录 一、launch启动程序 1.1 run_optimiser.launch标定优化程序 1.2 assess_results.launch重投影误差评估程序 二、主要代码 2.1 feature_extraction_node.cpp文件 2.2 feature_extractor.cpp文件 2.2.1 FeatureExtractor::callback_camerainfo函数 2.2.2 serviceCB函…
阅读更多...
QT快速操作Excel的实现介绍及操作类封装

QT快速操作Excel的实现介绍及操作类封装

QT中操作Excel还是比较简单的&#xff0c;Qt提供了QAxObject&#xff0c;包装COM组件的类&#xff0c;通过COM通过COM操作使用QAxObject类&#xff0c;使用此类&#xff0c;需要在pro文件中添加"QT　　 axcontainer "。 基本流程介绍 QAxObject&#xff1a; QAxObj…
阅读更多...
SAP从入门到放弃系列之pMRP

SAP从入门到放弃系列之pMRP

最近学习pMRP&#xff0c;查了很多博客&#xff0c;机翻一篇内容非常详细的文章&#xff0c;感谢大佬&#xff1a; 原文地址&#xff1a; pMRP–Predictive Material and Resource Planning in SAP S/4HANA : Step by Step execution pMRP https://blogs.sap.com/2020/04/14/p…
阅读更多...
机器学习【线性回归】

机器学习【线性回归】

机器学习【线性回归】 回归预测的结果是离散型变量&#xff0c;身高和年龄 损失函数&#xff1a;SSE&#xff08;误差平方和&#xff09;&#xff0c;RSS&#xff08;残差平方和&#xff09;&#xff0c;误差越大越差 最小二乘法&#xff1a;通过最小化真实值和预测值之间的…
阅读更多...
大数据：sparkSQL，历史，DataSet，DataFrame，sparkSession

大数据：sparkSQL，历史，DataSet，DataFrame，sparkSession

大数据&#xff1a;sparkSQL 2022找工作是学历、能力和运气的超强结合体&#xff0c;遇到寒冬&#xff0c;大厂不招人&#xff0c;可能很多算法学生都得去找开发&#xff0c;测开 测开的话&#xff0c;你就得学数据库&#xff0c;sql&#xff0c;oracle&#xff0c;尤其sql要学…
阅读更多...
第十章：创建和管理表

第十章：创建和管理表

第十章&#xff1a;创建和管理表 10.1&#xff1a;基础知识 一条数据存储的过程 ​ 存储数据是处理数据的第一步。只有正确地把数据存储起来&#xff0c;我们才能进行有效的处理和分析。否则&#xff0c;只能是一团乱麻&#xff0c;无从下手。 ​ 在MySQL中&#xff0c;一个完…
阅读更多...
使用模板方法模式封装协议消息

使用模板方法模式封装协议消息

目录 整体框架 模板方法介绍 关于本案例设计 c impl惯用法 cimpl惯用法好处 此案例impl惯用法的设计 关于序列化和反序列化 序列化和反序列化 本项目使用介绍 谷歌测试 谷歌测试环境 谷歌测试用例 完整源码地址 概述 本文介绍了从 设计模式之模板方法模式协议消…
阅读更多...
面对CPU狂飙时的5步解决方案

面对CPU狂飙时的5步解决方案

现在企业对后端开发的要求越来越高&#xff0c;不仅要求我们会写代码&#xff0c;还要我们能够进行部署和运维&#xff01; 项目上线并运行一段时间后&#xff0c;可能会发现部署所在的Linux服务器CPU占用过高&#xff0c;该如何排查解决&#xff1f; 本文用5步带你搞定线上CPU…
阅读更多...
操作系统-进程和线程-同步、互斥、死锁

操作系统-进程和线程-同步、互斥、死锁

目录 一、同步互斥 二、互斥的实现方法 2.1软件实现 2.1.1单标志法 2.1.2双标志先检查 2.1.3双标志后检查 2.1.4Petersons算法 2.2硬件实现 2.2.1 TestAndSet指令 2.2.2 Swap指令 三、信号量机制 3.1整形变量 3.2 记录型变量 3.3用信号量实现进程互斥、同步、前驱关系…
阅读更多...
Sui与F1甲骨文红牛车队达成合作

Sui与F1甲骨文红牛车队达成合作

在近期达成的一项为期多年的合作协议中&#xff0c;甲骨文红牛车队将利用Sui网络开发&#xff0c;为粉丝带来全新的数字化体验。 甲骨文红牛车队的粉丝将很快在Sui网络上体验到他们最爱的一级方程式车队带来的激情。最近几个赛季一直统治着F1赛场的甲骨文红牛车队&#xff0c;与…
阅读更多...
代码随想录算法训练营第五十三天 | 力扣 1143.最长公共子序列, 1035.不相交的线, 53. 最大子序和

代码随想录算法训练营第五十三天 | 力扣 1143.最长公共子序列, 1035.不相交的线, 53. 最大子序和

1143.最长公共子序列 题目 1143. 最长公共子序列 给定两个字符串 text1 和 text2&#xff0c;返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 &#xff0c;返回 0 。 一个字符串的 子序列 是指这样一个新的字符串&#xff1a;它是由原字符串在不改变字符…
阅读更多...
2022年值得关注的7个主要SD-WAN趋势

2022年值得关注的7个主要SD-WAN趋势

随着SD-WAN技术在2022年继续发展成熟&#xff0c;该技术在集成远程访问、自动化和多云连接方面的支持有望得到更多的改进。 软件定义WAN仍然是增强用户体验(UX)&#xff0c;提高安全性&#xff0c;以及提供与基于云计算的应用程序的连接的一项关键技术。 随着SD-WAN的成熟&…
阅读更多...
java设计模式之：原型模式

java设计模式之：原型模式

在我们的生活中&#xff0c;有很多例子&#xff0c;都是用到了原型模式&#xff0c;例如&#xff1a;我们去配钥匙的时候&#xff0c;肯定先要有一个原配钥匙才可以去配钥匙&#xff1b;《西游记》中孙悟空可以用猴毛根据自己的形象&#xff0c;复制&#xff08;又称“克隆”或…
阅读更多...
时间序列预测 | Matlab基于北方苍鹰算法优化随机森林(NGO-RF)与随机森林(RF)的时间序列预测对比

时间序列预测 | Matlab基于北方苍鹰算法优化随机森林(NGO-RF)与随机森林(RF)的时间序列预测对比

文章目录 效果一览文章概述部分源码参考资料效果一览 文章概述 时间序列预测 | Matlab基于北方苍鹰算法优化随机森林(NGO-RF)与随机森林(RF)的时间序列预测对比 评价指标包括:MAE、RMSE和R2等，代码质量极高，方便学习和替换数据。要求2018版本及以上。 部分源码 %-----------…
阅读更多...
【Apache-Flink零基础入门】「入门到精通系列」手把手+零基础带你玩转大数据流式处理引擎Flink（基础概念解析）

【Apache-Flink零基础入门】「入门到精通系列」手把手+零基础带你玩转大数据流式处理引擎Flink（基础概念解析）

手把手零基础带你玩转大数据流式处理引擎Flink 前言介绍Apache Flink 的定义、架构及原理Flink应用服务Streams有限数据流和无限数据流的区别 StateTimeAPI Flink架构体系 Flink操作处理Flink 的应用场景Flink 的应用场景&#xff1a;Data Pipeline实时数仓搜索引擎推荐 Flink …
阅读更多...
华为诺亚 VanillaNet

华为诺亚 VanillaNet

文章标题&#xff1a;《VanillaNet: the Power of Minimalism in Deep Learning》 文章地址&#xff1a;https://arxiv.org/abs/2305.12972 github地址&#xff1a;https://github.com/huawei-noah/VanillaNet 华为诺亚方舟实验室和悉尼大学&#xff0c;2023年5月代码刚开源的…
阅读更多...
基于HAL库的STM32的单定时器的多路输入捕获测量脉冲频率(外部时钟实现)

基于HAL库的STM32的单定时器的多路输入捕获测量脉冲频率(外部时钟实现)

目录 写在前面 一般的做法&#xff08;定时器单通道输入捕获) 以外部时钟的方式(高低频都适用) 测试效果 写在前面 STM32的定时器本身有输入捕获的功能。可选择双端捕获&#xff0c;上升沿捕获或者是下降沿捕获。对应捕获频率来说,连续捕获上升沿或下降沿的时间间隔就是其脉…
阅读更多...
手把手教你F103工程文件的创建并且通过protesu仿真验证创建工程文件的正确性（低成本）

手把手教你F103工程文件的创建并且通过protesu仿真验证创建工程文件的正确性（低成本）

目录 一、新建工程文件夹 二、新建一个工程框架 三、添加文件 四、仿真验证 五、仿真调试中遇到的问题并解决 一、新建工程文件夹 新建工程文件夹分为 2 个步骤&#xff1a;1&#xff0c;新建工程文件夹&#xff1b;2&#xff0c;拷贝工程相关文件。 1.新建工程文件 首先…
阅读更多...
【04】STM32·HAL库开发-MDK5使用技巧 |文本美化 | 代码编辑技巧 | 查找与替换技巧 | 编译问题定位 | 窗口视图初始化

【04】STM32·HAL库开发-MDK5使用技巧 |文本美化 | 代码编辑技巧 | 查找与替换技巧 | 编译问题定位 | 窗口视图初始化

目录 1.文本美化&#xff08;熟悉&#xff09;1.1编辑器设置1.2字体和颜色设置1.3用户关键字设置1.4代码提示&语法检测1.5global.prop文件妙用 2.代码编辑技巧&#xff08;熟悉&#xff09;2.1Tab键的妙用2.2快速定位函数或变量被定义的地方2.3快速注释&快速取消注释 3…
阅读更多...
python面向对象操作2（速通版）

python面向对象操作2（速通版）

目录 一、私有和公有属性的定义和使用 1.公有属性定义和使用 2.私有属性 二、继承 1.应用 2.子类不能用父类的私有方法 3.子类初始化父类 4.子类重写和调用父类方法 5.多层继承 6.多层继承-初始化过程 7.多继承基本格式 8.多层多继承时的初始化问题 9.多继承初始化…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023